はじめに
この記事はSP2LC Advent Calendar 2017 10日目の記事です.
SP2LCとの関わり
高専1年の時から参加しており,特にこだわりはなく広く浅く勉強しながら活動しています.
紹介理由
最近ググりながらコツコツ2Dの物理エンジンぽいものを作成しているのですが,その際に衝突判定などに使えるアルゴリズムとして出てきたので紹介してみようと思いました.
ミンコフスキー差とは(前提知識)
突然ミンコフスキー差と言われてもわからないと思いますが,これはGJKアルゴリズムの前提となっている考え方です.なのでまずミンコフスキー差について説明しようと思います.
ミンコフスキー差とは点の集合で表された2つの図形AとBがあった場合に図形Aを原点中心に反転させ,それを図形Bの周りを移動させた時に生じる領域のことです.言葉だとなかなかわかりにくいので下の図を見てください.
黄色い図形が図形A,青い図形が図形Bと考えてください.ちなみに黄色い図形にある黒丸は原点です. この場合に上での説明の通りに図形Aを原点中心に反転させるとだいたい下の図のようになります.  図形Aを原点中心に反転させるところまでやりました.次は図形Aを図形Bの周りで移動させます.この時の移動というのは,図形Aの原点だった場所を図形Bの各点に合わせて平行移動させることを言います.すると下の図のようになります.  結構アバウトに図を作っているので少しずれてたりしていますが,おおむね図のようになります.すると図形Bの周りを移動した図形Aによって領域を作ることができます.  黒の線で囲った領域が図形Aが移動したことによってできた領域になります.この領域のことがミンコフスキー差といい,GJKアルゴリズムの中でとても重要なものとなっています.本当はこのミンコフスキー差を一発で表現する数式などがありますが,なんとなくしかわかってないので割愛します.GJKアルゴリズムとは
はい.長々と説明しましたがやっと本題です.ではミンコフスキー差を使用してどうやって衝突判定をするのかというのを説明しようと思います.
GJKアルゴリズムとはミンコフスキー差のある特性を利用して衝突しているかを判定するアルゴリズムです.それはミンコフスキー差の領域内に原点が含まれていた場合ミンコフスキー差を求めた図形Aと図形Bは重なっているという特性です.
では実際にGJKアルゴリズムの動きを説明しようと思います.

まず任意の点Aから原点へのベクトルV1を伸ばします.そしてそのベクトル方向で一番遠い点を求めます.一番遠い点はサポート写像を使って求めますが今回は割愛します.
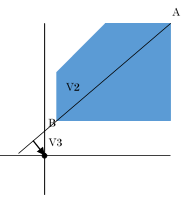
すると一番遠い点が点Bだということがわかります.次に起点とした点,今回でいうと点Aから点Bを通るように線分を伸ばします.この線分は線分ABとします.線分ABから原点への最短点を求め,その点から原点へのベクトルを求めます.今回はV3とします.

上で求めたベクトルV3の方向で一番遠い点を求めると点Cが得られます.すると,これで得た点がA・B・Cと3点求まったのでそれぞれをつないで三角形を作成します.そしてその三角形の中に原点が含まれているかを調べます.図の図形では含まれていないため処理を続行します.1つ前に求めた点であるBから今求めた点Cの線分を作成します.そして最短点を調べますが,図ではすでに最短点と原点をつなげたベクトルを作成しその方向に一番遠い点を調べても既に調べた後です.なので処理が終了します.
おわりに
自分でも最近なんとなくわかったかなという感じなので書いてて混乱しかけました.
今回は割愛した内容もあったりするので気になる人は調べてみるともっとわかりやすく説明している人がいるので,ぜひ調べてみてください.
