この記事は Web グラフィックス Advent Calendar 2022 の11目の記事です。

簡単にきれいなグラデーションがしたい

筆者は個人でドロー系のお絵かきツールを作っています。

前回は放射状グラデーション（RadialGradient）を細分割して線をはみ出さないようにしてみましたが、パフォーマンス面で問題がありました。放射状だけで塗ることに限界を感じたため、もっと他のアプローチを考えてみました。

考えてみると、イラストなどの絵を描くために塗りつぶしをする場合、ベタ塗りだけで用が足りるとは限りません。色や濃淡を変えながら塗るわけですが、できるだけ簡単にきれいにグラデーションさせることができたら嬉しいです。また、ドロー系ツールなので、後からデータを変更するのが楽であるという強みを生かしたいです。

４点グラデーション(Quad gradient)

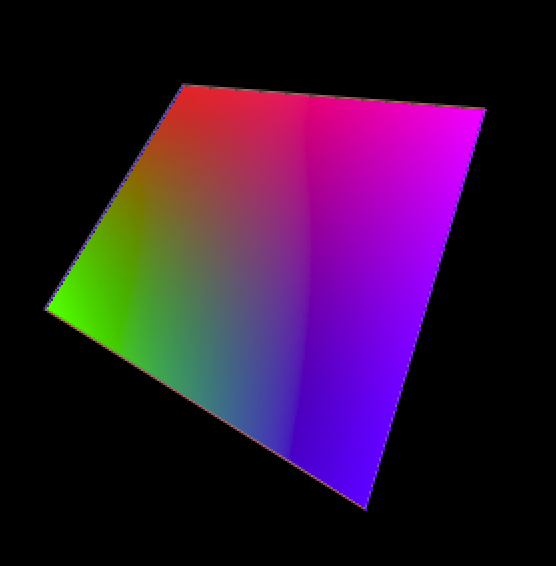
で、思い当たったのが、色を持った４つの頂点の間を補間して描画することです。これをここでは「４点グラデーション」と呼ぶことにします。

英語での呼称について

英語では Four point gradient とか Bilinear gradient とか Quad gradient 等と呼ばれるようです。CG技術の界隈では正方形にかぎらない四角形のことをQuadと呼ぶほうが伝わりやすいため、ここではその言葉を使います。

これなら編集データが少なくて楽ですし、頂点の位置をうまく調整すれば線をはみ出さないように塗ることができるかもしれません。また、頂点三つではなく四つなのは、グリッドとして並べることを想定しているからです。

描画処理の概要

アルゴリズムとしては、四角形の中のある点(x, y)に対応する正規化座標(t, u)を計算する、そして色の線形補間をする、という考え方で行きます。

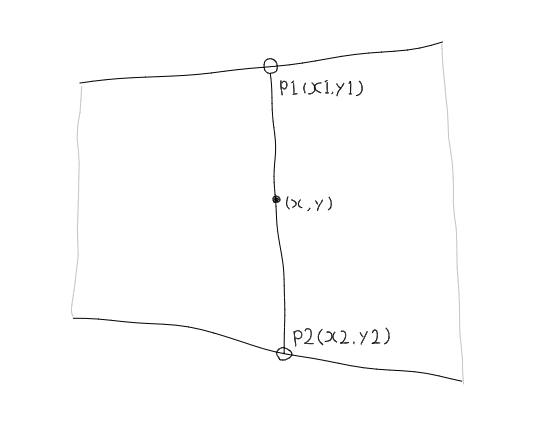
まず２辺を決め、その辺上の点をp1(x1, x2)、p2(x2, y2)とします。p1、p2の位置は一つの変数t(0.0～1.0)をパラメータとして線形補間されるものとします。

ここでp1、p2を通る直線を考えると、tがいずれかの値のときに(x, y)を通るはずです。とすると、次の式が成り立ちます。xa1などは２辺を表す直線のパラメータです。

x1 = xa1 * t + xb1
y1 = ya1 * t + yb1
x2 = xa2 * t + xb2
y2 = ya2 * t + yb2
y = (y2 - y1) / (x2 - x1) * (x - x1) + y1

最後の式にx1, y1, x2, y2を代入すると次の式が得られます。

y = (ya2 * t + yb2 - (ya1 * t + yb1)) / (xa2 * t + xb2 - (xa1 * t + xb1)) * (x - (xa1 * t + xb1)) + ya1 * t + yb1

これをtについて解けばいいわけですが、手作業でやるには（やってはみましたけど）難しいので数式ツールにかけて展開します。最終的に二次式になりますので、tの値を求めることができます。残りの２辺について同様に求めれば、uについても計算できます。

あとはtで２辺の色を線形補間して、得られた２色をさらにuで線形補間すれば(x,y)の色を計算することができます。

ついでにtとuが0.0～1.0の間であるかどうかで内外判定もできますので、四角形の中だけを塗りつぶすこともできますね。

ということで、何番煎じか知りませんが実装してみました。

実装したもの

Canvas2Dの機能だけではできないため、バイトデータの操作で実装しています。

See the Pen Canvas2D ４点グラデーションの実装実験 by 柏崎ワロタロ (@warotarock) on CodePen.

GPUを使ったCGのサンプルだと最初に虹色の三角形を描画することが多いですけど、四角形というのはわりと少ない気がします。そのためかちょっと新鮮な感じがしました。

まとめ

放射状グラデーションだけでは限界なので別の方法を考えた
４点グラデーションのアルゴリズムを考え、実装した
三角形のグラデーションと一味違うものを感じた（感想）

実はまだ続きます。次回、４点グラデーションでグリッドを描画します。
カレンダー埋まらないなー(笑)