この記事はkstm Advent Calendar 7日目です。
http://qiita.com/advent-calendar/2016/kstm

五色問題

　五色問題について実装する機会があったので記事にしました。
　この記事を書くに当たって「離散数学への招待(上)」を読みました。上巻の最終章で五色問題について証明されています。この証明を元にアルゴリズムを設計します。(この本では、演習問題5.4.5でアルゴリズムの設計が出題されています。)

問題概要

　この問題で与えられるグラフ$G$は頂点数は5以上、平面的とします。また、グラフは隣接リストで与えられます。

証明

　まず、$K_5$(5頂点の完全グラフ)を含まないことが題意からわかります。もし、$K_5$がグラフに含まれてしまうと平面的なグラフではなくなってしまいます。つまり、次数4のある頂点について、その隣接頂点を２頂点取り出した時、隣接していないものがある。つまり、隣接頂点のうち少なくとも２頂点は同じ色で彩色できることがわかる。次数4の頂点と4つの隣接頂点は４色で彩色できる。
　次に、次数が5の頂点$v$について考える。$v$についても$K_5$の部分グラフを作ることはないので、$v$の隣接頂点同士で隣接していない$x$、$y$が存在する。この時、辺$(v,x)$、$(v,y)$の縮約を考える。縮約によってできるグラフを$G'$新たな頂点を$w$とする。また、$G'$は平面的である。$x$、$y$以外の頂点を$t$、$u$、$z$とする。この時、以下の式が成り立つ。

c\left( s \right) \quad =\quad \begin{cases} c'\left( s \right)  & \quad \left( s\quad \notin \quad \{ x,y,v\}  \right)  \\ c'\left( w \right)  & \quad \left( s\quad =\quad x\quad or\quad s\quad =\quad y \right)  \\ i\quad \in \quad \{ 1,2,3,4,5\} \setminus \{ c'\left( w \right) ,c'\left( u \right) ,c'\left( t \right) ,c'\left( z \right) \}  & \quad \left( s\quad =\quad v \right)  \end{cases}

$c(s)$は頂点$c$の色を表す。また、上式は再帰的に成り立つので頂点数6以上のグラフで成り立つ。頂点数6以上のときは、$x$, $y$以外の$t$, $u$, $z$の部分が増える。

実装

　それぞれの頂点色を決めてから、networkxとmatplotlibを使って描画をします。

%matplotlib inline
import networkx as nx
import matplotlib.pyplot as plt

N = 9
E = [(1,2), (1,5), (2,3), (2,9), (3,9), (3,4), (4,9), (4,5), (4,6), (5, 9), (5,6), (6,7), (7,8),(2,5),(5,3)]
C = [-1 for i in range(N+1)] 
G = [[] for i in range(N+1)]

# 隣接リストの生成
def init_G(G, E):
    for (x, y) in E:
        G[x].append(y)
        G[y].append(x)
init_G(G, E)

# 色の決定
def init_C():
    # 頂点数の数え上げ
    count = 0
    for node in G:
        if len(node) > 0:
            count += 1

    # 頂点数4なら色を決定
    if count == 4:
        c = 1
        for (i, node) in enumerate(G):
            if len(node) > 0:
                C[i] = c
                c += 1
        return

    # vの決定
    pv = 0
    max_len_v = 0
    for (i, node) in enumerate(G):
        if len(node) > max_len_v:
            pv = i
            max_len_v = len(node)

    # x, yの決定
    px = -1
    py = -1
    for x in G[pv]:
        for y in G[pv]:
            if x == y :
                continue
            if x not in G[y]:
                px = x
                py = y

    # 頂点数5なら色を決定                     
    if count == 5:
        C[px] = 1
        C[py] = 1
        c = 2
        for i in range(len(G)):
            if (len(G[i]) > 0) and (i != px) and (i != py):
                C[i] = c
                c += 1
        return

    # 縮約(wの追加, 辺の張り替え)          
    G.append([])
    lenG = len(G)
    for x in G[px]:
        if (x != px) and (x != py) and (x != pv):
            G[len(G)-1].append(x)
    for y in G[py]:
         if (y != px) and (y != py) and (y != pv):
            G[len(G)-1].append(y)
    for v in G[pv]:
         if (v != px) and (v != py) and (v != pv):
            G[len(G)-1].append(v)

    for (i, node) in enumerate(G):
        if px in node:
            G[i].remove(px)
            G[i].append(lenG-1)
        if py in node:
            G[i].remove(py)
            G[i].append(lenG-1)
        if pv in node:
            G[i].remove(pv)
            G[i].append(lenG-1)

    for i in range(len(G)):
        G[i] = list(set(G[i]))
    G[px] = []
    G[py] = []
    G[pv] = []
    mG = list(G[lenG-1])

    C.append(-1)
    init_C()

    # x, y, vの色の決定
    C[px] = C[lenG-1]
    C[py] = C[lenG-1]  
    cv = [1,2,3,4,5]
    for i in mG:
        if C[i] in cv:
            cv.remove(C[i])
    cv.remove(C[lenG-1])
    C[pv] = cv[0]

init_C()

G=nx.Graph()
G.add_edges_from(E)

gcolor = ['blue', 'red', 'green', 'cyan', 'yellow']
lcolor = [gcolor[C[i]-1] for i in G.nodes()]

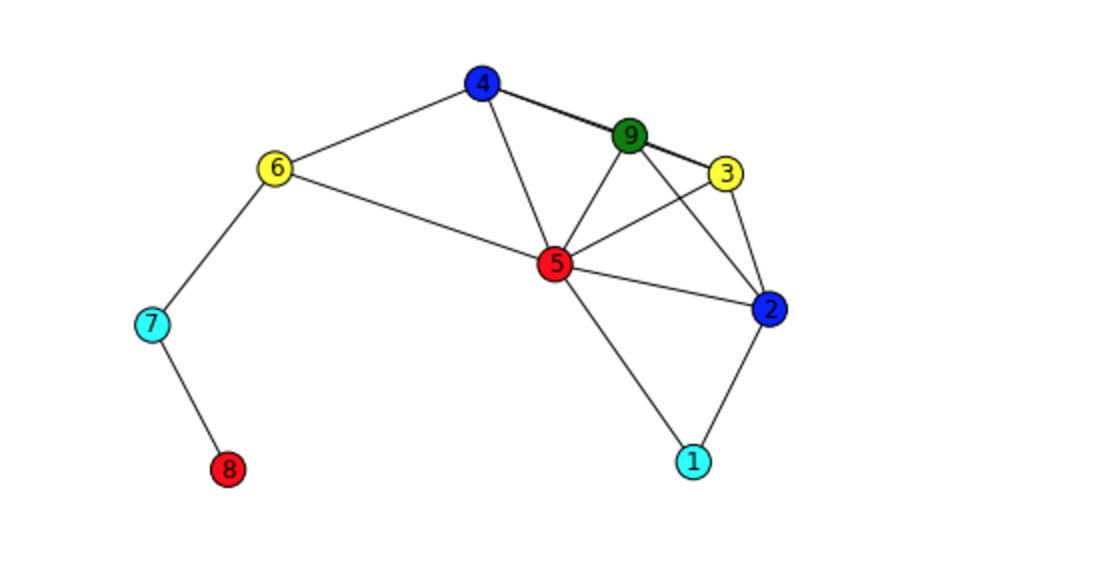
nx.draw(G, node_color = lcolor, with_labels = True)
plt.show()

こんな感じの色付きグラフが表示できるはずです。