パソコンでWindowsの方は、Ctrl+Fで検索したい文字列を検索することができるとおもいます。
このような文字列検索は、どんなアルゴリズムが使われて、どのように行われているのでしょうか?
今回はそれを見ていこうとおもいます。
力まかせのアルゴリズム
一番シンプルな方法です。
テキストを一番左から照合していき、一致しなかったらパターン(検索したい文字列)を右へずらしていって、テキストからはみ出るまで繰り返していくアルゴリズムです。
イメージしやすいように下の画像をご覧ください。
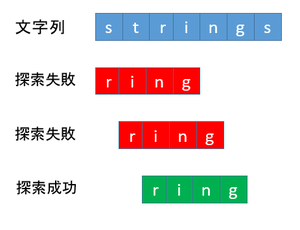
【参照】
https://engineeringnote.hateblo.jp/entry/python/algorithm-and-data-structures/brute_force_algorithm より引用
単純でわかりやすいアルゴリズムですが、これだと計算量が増えてしまうんです。もしこれが、何百という文字列で、最後のほうに一致する文字列があったら、効率悪いですよね。
それにこのアルゴリズムは照合する場所がイチイチ先頭に戻ってしまうので、その点も非効率であると言えます。
最悪計算量は、O(MN)になるんです。
実際にはこれほどの計算量になることは少ないので、O(N)に落ち着くようですけどね。
この力まかせのアルゴリズムを改良したものがKMP法というアルゴリズムです。
KMP法
結論からいうと、テキストとパターンで重なっている部分を効率よく見つけ出し、
照合を再開する位置を求め、パターンの移動をなるべく大きくするアルゴリズムです。
実際に例を見た方が早いとおもいますので、以下の画像をご覧ください。

上が文字列で、下がパターンです。
ここでよく見てみると、パターンのABと文字列の二番目のABが一致していることが分かります。
画像で表すと以下のようになります。
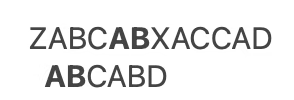
つまり、2つ目のABから照合を始めれば、CABDが一致しているかどうかを調べればいいので、
力まかせのアルゴリズムより効率がいいですね。
しかし、実際にはどれだけパターンをずらしているか、というずらしテーブルを作成しなければならないので、ときには力まかせのアルゴリズムの方が効率がいい場合があります。
ボイヤー・ムーア法
このアルゴリズムの特徴は、文字列の末尾から参照するという部分です。
以下の画像のようにしていきます。
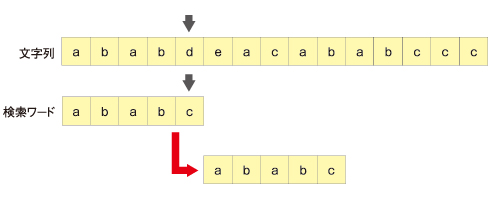
https://atmarkit.itmedia.co.jp/ait/articles/0902/04/news144_3.html より引用
このように検索ワードの末尾と、検索ワードが一致しなかった場合、検索ワードの先頭から文字数分だけ移動します。
上記の画像でいえば、先頭のaからみて5文字分移動するような感じです。
移動すると今度は以下の画像のようになります。
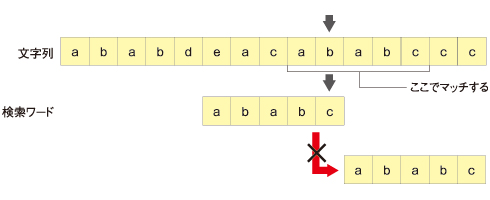
https://atmarkit.itmedia.co.jp/ait/articles/0902/04/news144_3.html より引用
今回も末尾同士は一致してはいませんが、ここで注意が必要です。文字列の末尾の文字が、検索ワードの中に入ってる場合は、それと文字列の末尾を一致させるようにしなくてはなりません。
一致しているのに見逃してしまう可能性があるからです。
このように文字列を見ていくアルゴリズムをボイヤー・ムーア法といいます。
このアルゴリズムが今回紹介したアルゴリズムの中で一番計算量が少ないようです。
以上です。何か間違いがございましたら、ご教示いただけますと幸いです。
【参考記事】