時間計算量
アルゴリズムの速さを決めるものには空間計算量と時間計算量があります。
違いとしては、
➀時間計算量(処理時間の計算量)
➁空間計算量(メモリ使用量の計算量)
単に計算量(オーダー)と言った場合、時間計算量のことを指します。
O(オー)記法
時間計算量を考えるとき、O記法というのがあります。
O記法とは、そのアルゴリズムがどれくらいの計算量になるのかをザックリ示すものです。
計算結果は、大体この辺の計算量に落ち着くだろう、というものです。
対数をつかったり、使わなかったりすることで計算量が変わってくることが多々あります。
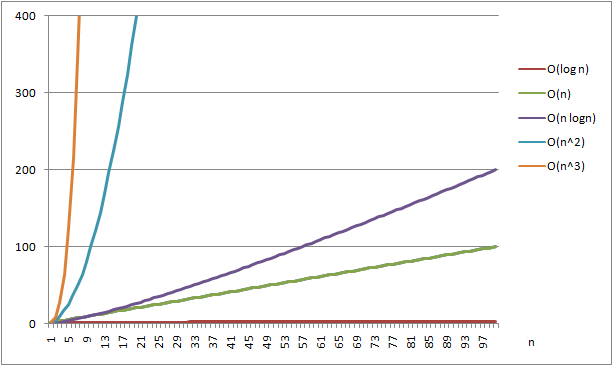
https://www.google.com/url?sa=i&url=http%3A%2F%2Fsevendays-study.com%2Falgorithm%2Fex-day1.html&psig=AOvVaw0x1McBE72gSInQyfF43EaV&ust=1649055804570000&source=images&cd=vfe&ved=0CAwQjhxqFwoTCMCGxd6p9_YCFQAAAAAdAAAAABA6 より引用
基本的にO(logn)を使うことでnの数が増えても、処理速度は減らないような気がしました。
3つのアルゴリズムの計算量
代表的な3つのアルゴリズムをもとに計算量を比べていこうとおもいます
バブルソート
バブルソートをよく知らないという方はこちらを参考にしてみてください。
バブルソートは、以下の画像のような流れに沿って行われます。
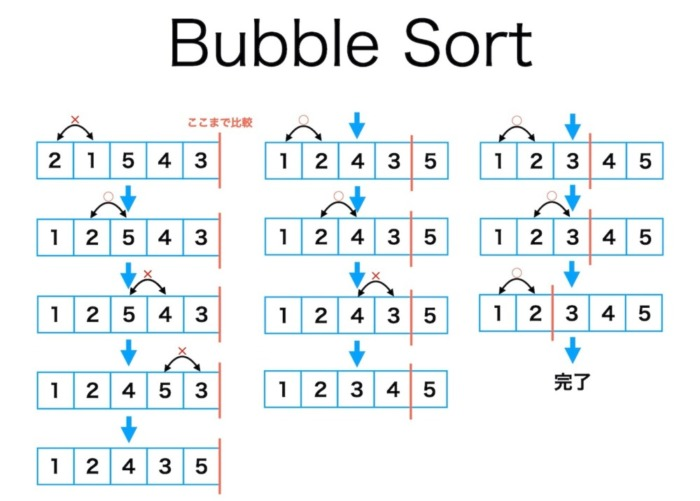
https://www.google.com/url?sa=i&url=https%3A%2F%2Ffree-engineer.life%2Fbubble-sort%2F&psig=AOvVaw1gkzZoK9sYmMxNk1Y7_Zo1&ust=1649056471298000&source=images&cd=vfe&ved=0CAwQjhxqFwoTCKiAyJ6s9_YCFQAAAAAdAAAAABAU より引用
計算量は1個ずつ減っていってることが分かりますね。
データサイズがn個だとすると、n-1,n-2,n-3,となっていき、計算量はO(n^2)となります。
先ほどの例を見ても、たしかにデータ量の2乗分の計算量を持っていますね。
これだとデータ量が10になっただけで、100の計算量を持ってしまうので、あまりいいアルゴリズムではないですね。
選択ソート
選択ソートが分からない方はこちらをご覧ください。
こちらもバブルソートと同じく計算量はO(n^2)となります。ですが、バブルソートより交換回数が少ないので、バブルソートよりも処理速度は速いです。
クイックソート
クイックソートが分からない方はこちらをご覧ください。
計算量はO(nlogn)となります。クイックソートは効率がよいアルゴリズムですが、このアルゴリズムにもデメリットはあります。
ピボットをどこにするかで効率は決まってしまいますが、この的確なピボットを計算するのが大変らしいです。
【参考記事】