５等分のシフト埋め

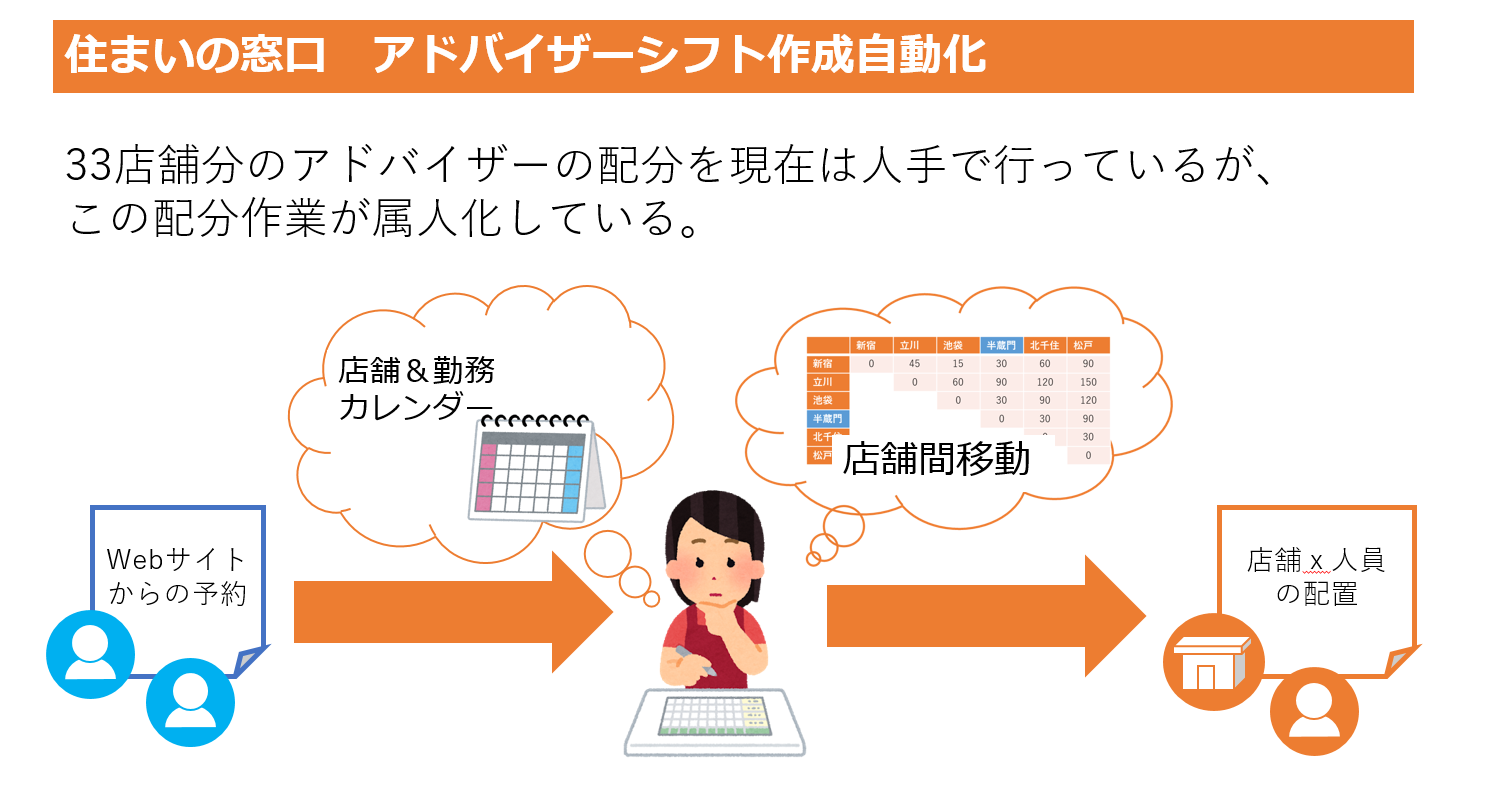
背景

私が所属しているAI戦略室では、社内で"AIお悩み相談会"を開催し「こんなことってできない？」というニーズに対して既存のツールやライブラリを組み合わせて解決策を探る、という業務も行っています。

例えば、 LIFULL HOME'S 住まいの窓口 というサービスがあります。これは、家づくりや住まい探しを、専属の住まい探しアドバイザーに無料で相談できるというサービスです。

この住まい探しアドバイザーのシフトを組む仕組みを自動化・最適化できないか？という問い合わせがあり、そこで見つけたGoogle ORtools の使い方の一つを今日はご紹介します。

例題

• あなたは5人の住まい探しアドバイザーのシフトを組むことになりました。
  • 図示するときに便利なので、仮に一花、二乃、三玖、四葉、五月という名前をつけます。
• 問題を簡略化するため、1店舗のシフトだけを考えればいいとします。
• 1日3枠×7日間の予約可能な枠があります。
  • 相談室は1つしかなく、同時に2人が顧客対応する（予約を受ける）ことはできないとします。
  • 相談業務はハードなので、アドバイザーは1日1枠しかシフトを入れることができないとします。
• 5人の間には、なるべく時間の偏りが出ないほうが望ましいです。
• アドバイザーの出勤希望を、なるべく満たすようにシフトを組むのが望ましいです。

制約充足問題として解く

このようなスケジューリングの問題は、制約充足問題（CSP）として解けることがあります。

満たすべき条件がいくつか課されていますが、大きく

• その制約(constraint)を満たせば良い条件
• 最適化(optimize)したい条件

に分けて考えることができれば、あとはソルバを使って解けます。

制約条件を満たす解をソルバに算出してもらい、あとは最適化したい条件を指定すればよいのです。
ここでは、

• 同時に2人は同じシフトに入れない
• アドバイザーは1日1枠しかシフトに入れない
• なるべく時間の偏りが出ないようにする

という条件を制約条件にして、

• アドバイザーの出勤希望をなるべく多く叶える

という値を最適化することにします。

モデルを宣言する

まず、ソルバーのモデルを用意します。
ここでは、CP-SATモデルを使います。
詳細は https://developers.google.com/optimization/cp/cp_solver をごらんください。

from ortools.sat.python import cp_model

model = cp_model.CpModel()

変数を用意する

次に、スケジューリングのフラグに使うための変数を用意します。

n人のアドバイザーに対し、d日間、s枠のシフトを組んだとすると、例えば以下のようなシフト表ができますね。

上の表を計算結果として出力するために、以下のように分解して、n, d, s の「3次元配列状」にすれば、

• その要素に1が入っていれば出勤する
• 0が入っていれば出勤しない

とみなすことができます。

つまり、n, d, sの「3次元配列」のどこにフラグをたてるか、という問題に落とし込めたわけです。

今回の例題に沿って、定数を定義してみます。

    num_advisers = 5
    num_shifts = 3
    days = ["日", "月", "火", "水", "木", "金", "土"]
    num_days = len(days)
    adviser_name = ["五月", "一花", "二乃", "三玖", "四葉"]
    all_advisers = range(num_advisers)
    all_shifts = range(num_shifts)
    all_days = range(num_days)

0 or 1のフラグを立ててソルバに解いてもらうための変数は、'ortools.sat.python.cp_model.IntVar'クラスのインスタンスとして作るので、dictを使って擬似的に多次元配列っぽく使えるものを用意します。

    shifts = {}
    for n in all_advisers:
        for d in all_days:
            for s in all_shifts:
                shifts[(n, d, s)] = model.NewBoolVar('shift_n%id%is%i' % (n, d, s))

制約条件を入れる

制約条件はmodel.Add()で入れていきます。

同時に2人は同じシフトに入れない：
「3次元配列」の図を"上"から見たときに、1つしかフラグが立っていないようにします。

    for d in all_days:
        for s in all_shifts:
            model.Add(sum(shifts[(n, d, s)] for n in all_advisers) == 1)

アドバイザーは1日1枠しかシフトに入れない:
「3次元配列」の図を"前"から見たときに、1つしかフラグが立っていないようにします。

    for n in all_advisers:
        for d in all_days:
            model.Add(sum(shifts[(n, d, s)] for s in all_shifts) <= 1)

なるべく時間の偏りが出ないようにする:
3 × 7 = 21枠あるのだから、21//5 = 4 枠を下限にして、
(21//5) + 1 = 5枠をアドバイザーごとの上限にすれば偏りが出なそうですね。
「3次元配列」の図で、アドバイザーごとの平面の表のフラグの数を全部足して、その結果が下限の制約値以上、上限の制約値以下になるようにします。

    min_shifts_per_adviser = (num_shifts * num_days) // num_advisers
    max_shifts_per_adviser = min_shifts_per_adviser + 1
    for n in all_advisers:
        num_shifts_worked = sum(
            shifts[(n, d, s)] for d in all_days for s in all_shifts)
        model.Add(min_shifts_per_adviser <= num_shifts_worked)
        model.Add(num_shifts_worked <= max_shifts_per_adviser)

時間帯の希望を受け付ける

次に、「この日のこのシフトに入りたい！」という希望を数値化します。こちらは素の0 or 1の値でいいので素直に多次元配列として用意します。

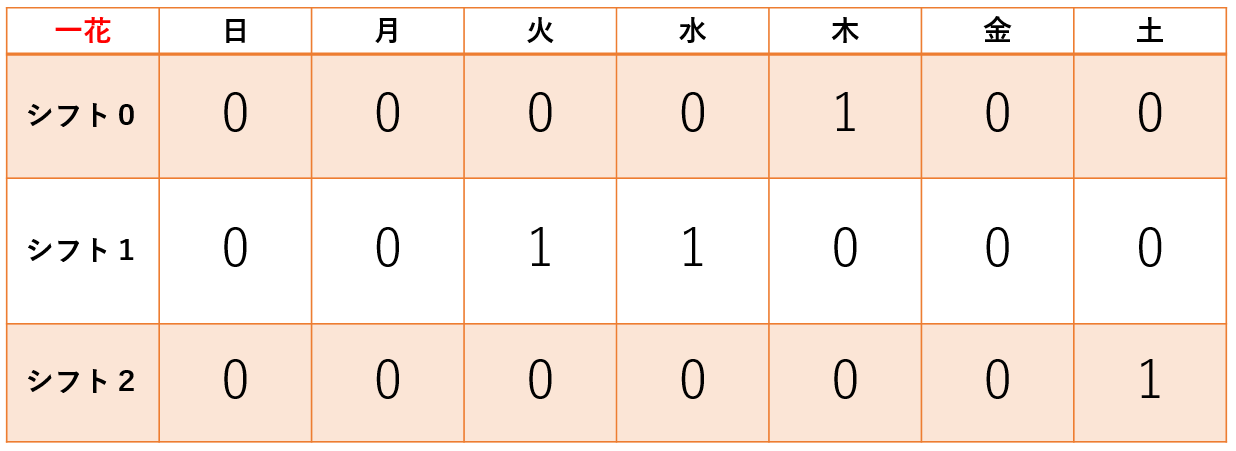
• その要素に1が入っていれば出勤希望
• その要素に0が入っていれば出勤希望ではない

ことにすると、以下のような3次元配列として５人分のシフト希望が数値化できます。

    shift_requests = [
            [[0, 0, 1], [0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 1], [0, 1, 0], [0, 0, 1]],
            [[0, 0, 0], [0, 0, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0], [0, 0, 0], [0, 0, 1]],   # 一花
            [[0, 1, 0], [0, 1, 0], [0, 0, 0], [1, 0, 0], [0, 0, 0], [0, 1, 0], [0, 0, 0]],
            [[0, 0, 1], [0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 0], [1, 0, 0], [0, 0, 0]],
            [[0, 0, 0], [0, 0, 1], [0, 1, 0], [0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 0]]
            ]

ここで、shiftsに値が入っているとき、shift_requests[n][d][s] * shifts[(n, d, s)] の計算を各要素ごとに行うと、
「その要素がアドバイザーの希望を満たせた場合」のみ計算結果が1になります。
これをmodel.Maximizeという関数に渡してあげることで、最適化条件をソルバに指示することができます。

    model.Maximize(
        sum(shift_requests[n][d][s] * shifts[(n, d, s)] for n in all_advisers
            for d in all_days for s in all_shifts))

プログラム全体

from ortools.sat.python import cp_model


def main():
    # This program tries to find an optimal assignment of advisers to shifts
    # (3 shifts per day, for 7 days), subject to some constraints (see below).
    # Each adviser can request to be assigned to specific shifts.
    # The optimal assignment maximizes the number of fulfilled shift requests.
    num_advisers = 5
    num_shifts = 3
    days = ["日", "月", "火", "水", "木", "金", "土"]
    num_days = len(days)
    adviser_name = ["五月", "一花", "二乃", "三玖", "四葉"]
    all_advisers = range(num_advisers)
    all_shifts = range(num_shifts)
    all_days = range(num_days)
    shift_requests = [
            [[0, 0, 1], [0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 1], [0, 1, 0], [0, 0, 1]],
            [[0, 0, 0], [0, 0, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0], [0, 0, 0], [0, 0, 1]],
            [[0, 1, 0], [0, 1, 0], [0, 0, 0], [1, 0, 0], [0, 0, 0], [0, 1, 0], [0, 0, 0]],
            [[0, 0, 1], [0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 0], [1, 0, 0], [0, 0, 0]],
            [[0, 0, 0], [0, 0, 1], [0, 1, 0], [0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 0]]
            ]
    # Creates the model.
    model = cp_model.CpModel()

    # Creates shift variables.
    # shifts[(n, d, s)]: adviser 'n' works shift 's' on day 'd'.
    shifts = {}
    for n in all_advisers:
        for d in all_days:
            for s in all_shifts:
                shifts[(n, d, s)] = model.NewBoolVar('shift_n%id%is%i' % (n, d, s))

    # Each shift is assigned to exactly one adviser in .
    for d in all_days:
        for s in all_shifts:
            model.Add(sum(shifts[(n, d, s)] for n in all_advisers) == 1)

    # Each adviser works at most one shift per day.
    for n in all_advisers:
        for d in all_days:
            model.Add(sum(shifts[(n, d, s)] for s in all_shifts) <= 1)

    # min_shifts_assigned is the largest integer such that every adviser can be
    # assigned at least that number of shifts.
    min_shifts_per_adviser = (num_shifts * num_days) // num_advisers
    max_shifts_per_adviser = min_shifts_per_adviser + 1
    for n in all_advisers:
        num_shifts_worked = sum(
            shifts[(n, d, s)] for d in all_days for s in all_shifts)
        model.Add(min_shifts_per_adviser <= num_shifts_worked)
        model.Add(num_shifts_worked <= max_shifts_per_adviser)

    model.Maximize(
        sum(shift_requests[n][d][s] * shifts[(n, d, s)] for n in all_advisers
            for d in all_days for s in all_shifts))
    # Creates the solver and solve.
    solver = cp_model.CpSolver()
    solver.Solve(model)
    for d in all_days:
        print(days[d] + "曜日:")
        for s in all_shifts:
            for n in all_advisers:
                if solver.Value(shifts[(n, d, s)]) == 1:
                    if shift_requests[n][d][s] == 1:
                        print('Adviser', adviser_name[n], 'works shift', s, '(requested).')
                    else:
                        print('Adviser', adviser_name[n], 'works shift', s, '(not requested).')
        print()

    # Statistics.
    print()
    print('Statistics')
    print('  - Number of shift requests met = %i' % solver.ObjectiveValue(), '(out of', num_advisers * min_shifts_per_adviser, ')')
    print('  - wall time       : %f s' % solver.WallTime())


if __name__ == '__main__':
    main()

##出力結果:

日曜日:
Adviser 四葉 works shift 0 (not requested).
Adviser 二乃 works shift 1 (requested).
Adviser 三玖 works shift 2 (requested).

月曜日:
Adviser 一花 works shift 0 (not requested).
Adviser 二乃 works shift 1 (requested).
Adviser 四葉 works shift 2 (requested).

火曜日:
Adviser 三玖 works shift 0 (requested).
Adviser 一花 works shift 1 (requested).
Adviser 四葉 works shift 2 (not requested).

水曜日:
Adviser 二乃 works shift 0 (requested).
Adviser 一花 works shift 1 (requested).
Adviser 五月 works shift 2 (not requested).

木曜日:
Adviser 四葉 works shift 0 (requested).
Adviser 三玖 works shift 1 (not requested).
Adviser 五月 works shift 2 (requested).

金曜日:
Adviser 三玖 works shift 0 (requested).
Adviser 五月 works shift 1 (requested).
Adviser 一花 works shift 2 (not requested).

土曜日:
Adviser 二乃 works shift 0 (not requested).
Adviser 四葉 works shift 1 (not requested).
Adviser 五月 works shift 2 (requested).


Statistics
  - Number of shift requests met = 13 (out of 20 )
  - wall time       : 0.007237 s

アドバイザーのシフト希望をもっとも満たした解が出力できました。

Enjoy!