Bellman-Ford法の解説

皆さんこんにちは。wakimikoです。
今回はグラフで使うBellman-Ford法について解説します。

#Bellman-Ford法とは
Bellman-Ford法とは、グラフの二点間の最短距離を求めるアルゴリズムです。
Dijkstra法と比べて辺の重みが負でも動きますが、重みに負の数がないならDijkstra法を使った方が高速です。
負の閉路があると正しい距離を求められませんが、負の閉路があることを検出できます。
頂点の数をV、辺の数をEとした場合、計算量は$O(|V||E|)$になります。

#コード例（C++）

#include <iostream>
#include <algorithm> //fillを使うため
#include <vector>

using namespace std;

#define MAX_V 1000
#define INF 10000000

struct edge {
    int from; //出発点
    int to;   //到達点
    int cost; //移動コスト
};

int main()
{
    int V; //頂点の数
    int side; //辺の数
    int S; //始点
    int G; //終点
    int d[MAX_V]; //始点から添え字の頂点に行くのにかかるコスト
    vector<edge> edges; //移動の情報を保存する

	cout << "頂点の数:";
    cin >> V;
	cout << "辺の数:";
	cin >> side;
	cout << "始点:";
	cin >> S;
	cout << "終点:";
	cin >> G;
	
	fill(d, d+V, INF); //すべての頂点をINFにする
    d[S] = 0; //始点を0にする

    for (int i = 0; i < side; i++) {
        struct edge add;
		cout << "出発点:";
        cin >> add.from;
		cout << "到達点:";
		cin >> add.to;
		cout << "移動コスト";
		cin >> add.cost;
		edges.push_back(add);
    }

    for (int i = 0; i < V; i++) {
        for (int j = 0; j < (int)edges.size(); j++) {
        
            struct edge e = edges[j];

            if (d[e.to] > d[e.from] + e.cost) {  //移動した後のコストが小さいと、頂点のコストを更新
                d[e.to] = d[e.from] + e.cost;
                if (i == V-1) {         //頂点の数と同じ回数ループすると、負の閉路があるのでループをぬける
                    cout << "negative loop" << endl;
                    break;
                } 
            }
        }
    }

    cout << "\n頂点" << S << "から頂点" << G << "まで移動するのにかかるコストの最小は" << d[G] << endl;
}

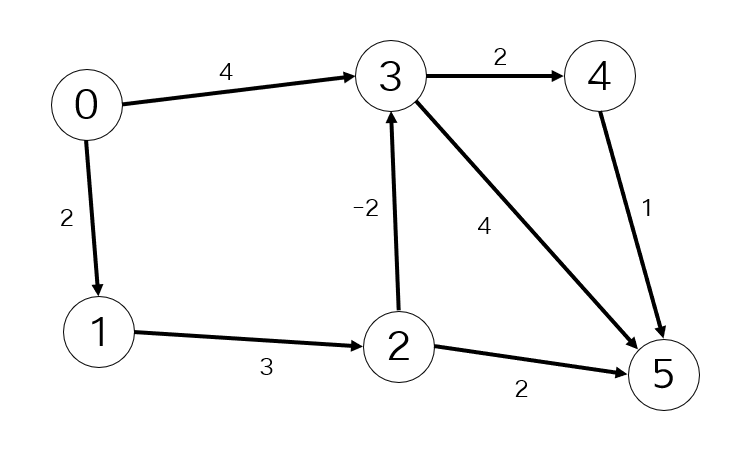
入力例として、次の有向グラフで頂点0から頂点5に移動するときの最小コストを考えてみましょう。

入力すると、次のようになります。

頂点の数:6
辺の数:8
始点:0
終点:5
出発点:0
到達点:1
移動コスト:2
出発点:0
到達点:3
移動コスト:4
出発点:1
到達点:2
移動コスト:3
出発点:2
到達点:3
移動コスト:-2
出発点:2
到達点:5
移動コスト:2
出発点:3
到達点:4
移動コスト:2
出発点:3
到達点:5
移動コスト:4
出発点:4
到達点:5
移動コスト:1

頂点0から頂点5まで移動するのにかかるコストの最小は6です

#動きの説明
まず、すべての頂点をINFで初期化して始点を0にします。

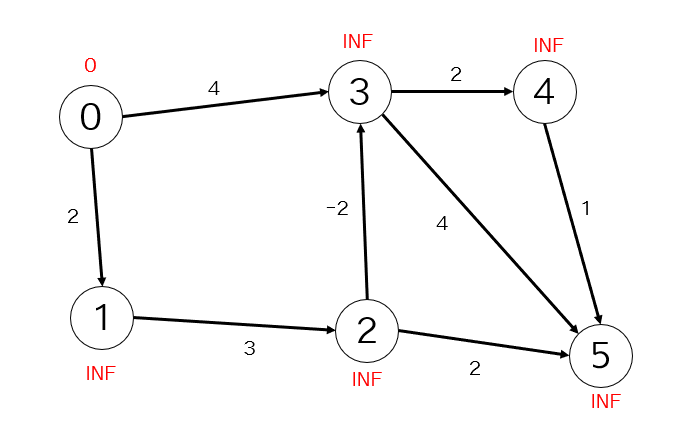
次に、入力された辺とコストの情報をもとに頂点を更新していきます。

１．出発点:0 到達点:1 移動コスト:2

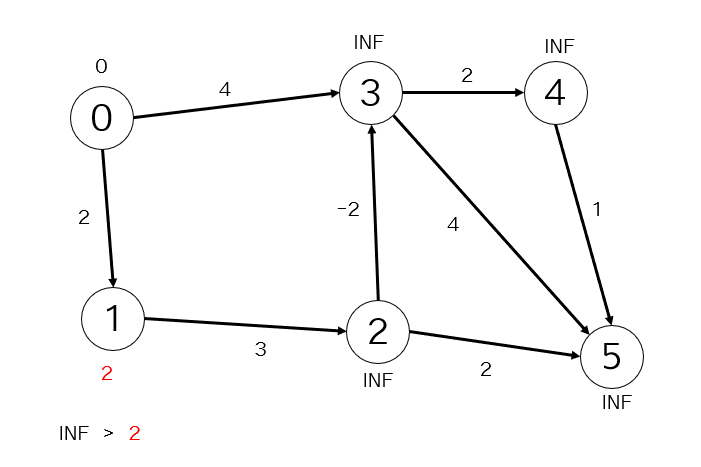
INFよりも移動にかかったコスト2の方が少ないので2で更新します。

２．出発点:0 到達点:3 移動コスト:4

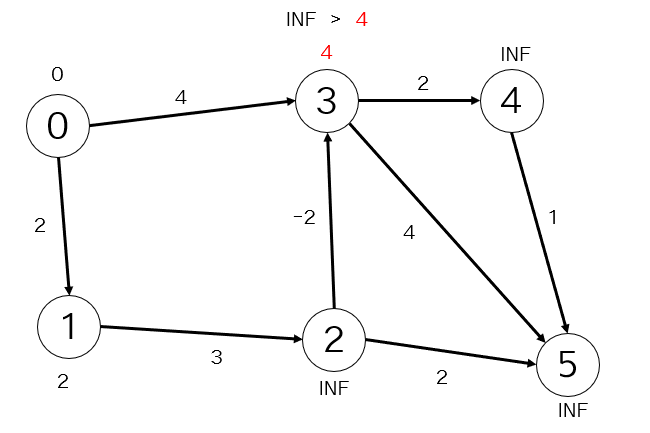
先ほどと同じように比較して、新しい情報の方がかかるコストが少ないので更新します。

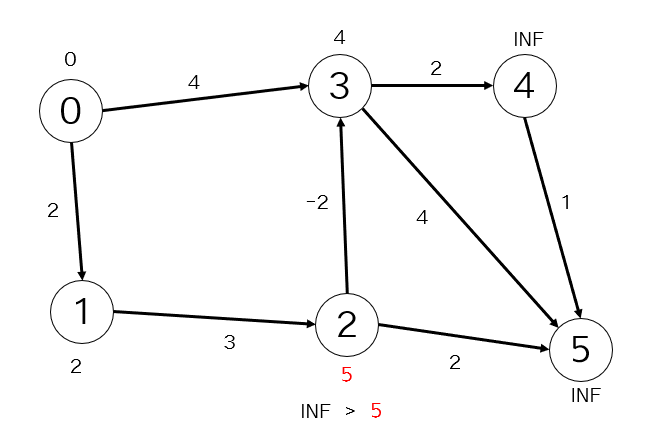
３．出発点:1 到達点:2 移動コスト:3

４．出発点:2 到達点:3 移動コスト:-2

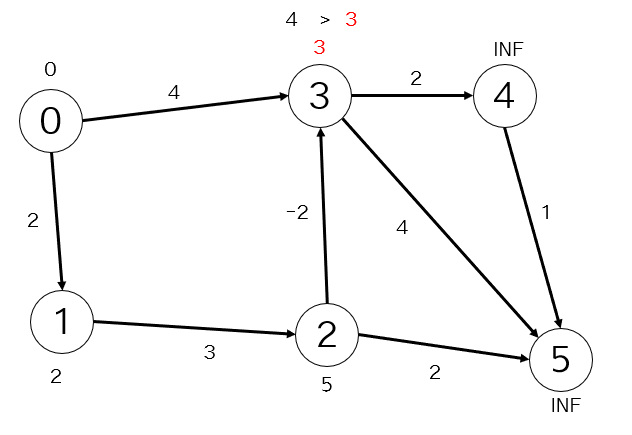
２．で更新した値よりも小さい値になったので頂点を更新します。

このように、すべての頂点について値を更新していくと次のようになります。

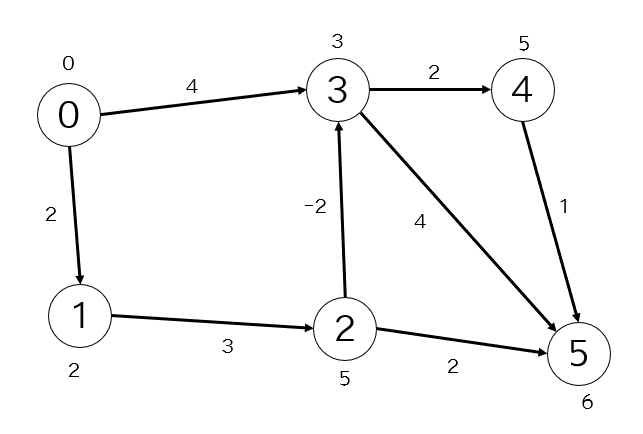
辺の情報をすべて見ることを１ループとすると、１ループするたびに最低でも１つの頂点についての最短距離は求まるので、頂点の数を$V$とすると$V-1$回のループでグラフ全体の最短距離を求めることができます。
（$V-1$になる理由は始点はループする前に0と決定しているため。)
そのため、$V$回目のループで頂点の更新があった場合はそのグラフに負の閉路があることになります。

#まとめ
・負の閉路があると正しく動かない場合がある。
・辺の重みが負でないならDijkstra法の方が高速。
・辺の情報についてのループを$V-1$回で全体の最短距離を求められる
・$V$回目のループで更新した場合はグラフに負の閉路がある