多重共線性

Last updated at 2023-12-14Posted at 2021-09-15

この記事を読んで分かること

多重共線性とは何か
これが起こるとどうなるのか
どのようなモデルや状況で起こるのか
これを解消するためにはどうすればいいのか.

多重共線性とは

多重共線性とは、データの中に相関が強いものが含まれていて、重回帰分析の性能が低下してしまうこと。
重回帰分析以外のモデル、決定木やsvm, ニューラルネットなど機械学習モデルに関しては起こらない。
理由を簡単に補足すると、これらのモデルは$y=a_1x_1+a_2x_2 \cdots a_n*x_n$のような関係式で表現されないためである。

相関を簡単に説明すると、あるデータ間で似たような傾向を持つということである。
また、相関の強さを表現する指標に相関係数というものがある。これは次の節で紹介する。
ここで多重共線性が起こりうるデータの例をあげる。
例えば、日本においては、年収と年齢は相関関係にある。国税庁のサイトより引用
つまり、年齢が大きいほど年収は大きい。

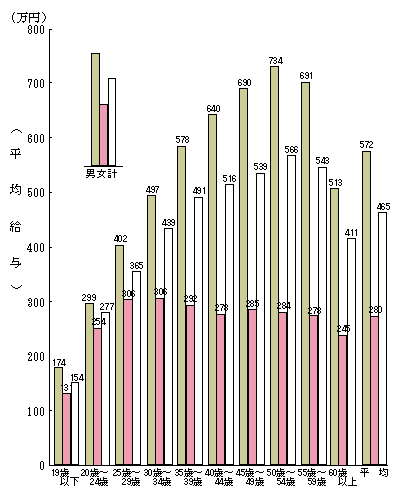
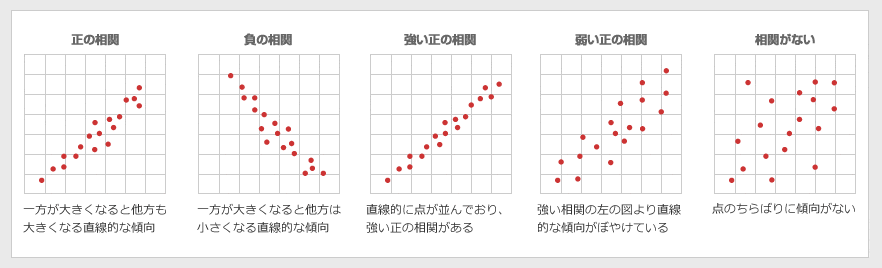
グラフで表現する場合、相関係数が大きいものはy=xに近く、小さいものは、y=-xに近い。また0の場合は、傾向が見られないようなランダムな配置になっている。
相関の強さとしては、絶対値をとって1に近いもの。つまり相関係数が小さいものも多重共線性が起こりうるので注意が必要である。

相関の大きさを表現する値（相関係数）

相関係数には、いくつかの種類がある。皆さんが高校までで習って一般的に知っているものはピアソンの相関係数である。
これらに共通する特徴としては、

-1~1の範囲を取る実数。
値が大きい(1に近い）ほど相関が大きく、小さいほど相関が小さい。
相関の強さは、絶対値を取ったときに値が大きいものである。(最小が０、最大が１）

これらのうち、ピアソンの相関係数と、スピアマンの順序相関について簡単に説明する。
前者は、一般的によく使う指標。後者は、変数にカテゴリが含まれているときによく使うものである。

ピアソンの相関係数

一般的に使われている尺度がピアソンの相関係数。
これは、2つの連続変数間の線形関係を評価する。一方の変数が変化したときにもう一方の変数が比例して変化する場合、関係は線形になる。
この指標は、-1~1の間を動き、大きいほど相関が正であるという。
強さを知りたいときは、絶対値をとって1に近いほど強いという。

スピアマンの相関係数

次に紹介するのが、スピアマンの順序相関係数。
こちらは一言で言うと、カテゴリ変数に対しても相関を見れるというもの。
上記のピアソンの相関係数は、連続値についてのみ定めたものだが、こちらの相関係数は、カテゴリ変数である順序尺度の変数についても定義できる。

引用元

多重共線性があると起こること

多重共線性があると、相関が強いデータ間の挙動がおかしくなり、モデルの安定性が欠如してしまう。
解釈としては、変数が一つ足らない(同じものが二つ入っているため)のでうまく方程式を解くことができないと解釈できる。

ランダムシードを変えるごとに、モデルの性能が大幅に変化してしまい、試行ごとに異なった性能のモデルとなってしまう。
これでは、汎化性能と言った話はできそうもない。

多重共線性の解消法

非常にシンプルだが、相関が強いデータを取り除けば良い。
相関の強さについてだが、相関係数というものを見るのが一般的である。

ここで、相関が強いはどの程度かという疑問が挙げられるだろうが、一般的な回答は現在存在しない。
なので各自で判断する必要がある。
また、これは必ず取り除かなければいけないというよりも、取り除いた方が性能が良くなるなら取り除くべきである、程度なので注意が必要である。（一般的には、変数は多いほどいいので（情報量が多いから）、不必要に取り除かなくて良い）

どうしても両方使いたい場合

どうしても片方を削除せず、両方使いたい場合の対処としては、主成分分析を行うと良いかもしれない。
これによって、複数の変数を一つにまとめることができ、両方を考慮しつつより良いモデルの構築ができる。

まとめ

多重共線性は重回帰分析に起こる現象。
これが起こるとモデルの汎化性能が下がる。
解消するためには、相関が強い変数を除けば良い。

参考文献

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up