【Unity】音声データからピッチ推定を行う

はじめに

本記事はAdvent Calendar 2022の18日目の記事です。

音声データを扱うための前提知識

本記事は、Unityに関するものではあるが、「音声データ」というある程度ゲーム開発では馴染みのないものを扱うので、いくらか必要な知識が出てきます。
ここでは、厳密性にはあまり捉われず、理解しやすい形で広く浅くこれらを説明していきます。
すでに知っている方や、Unityでの実装部だけ知りたい方は、読み飛ばしちゃってください。

音声信号とは

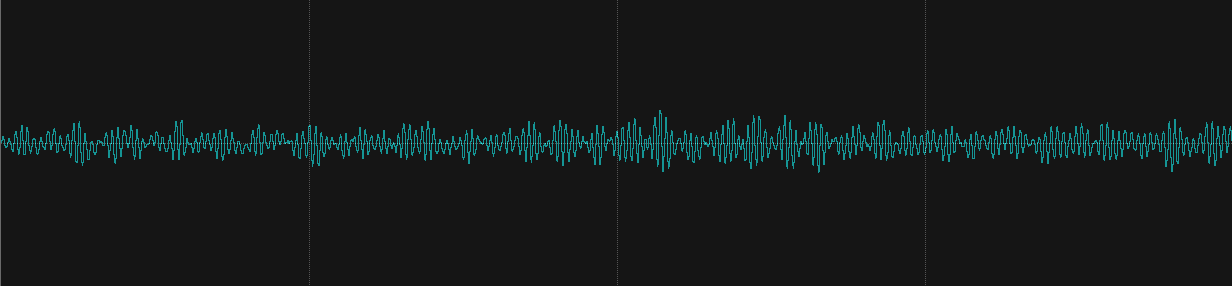
音が空気の振動であることをご存知の方は多いと思います。音を電気信号に変換する装置がマイクです。マイクによって、その瞬間の音の振動の強度が電圧に変換されます。この電圧は時間によって変化するので、言い換えると、音声の信号は、時間と振幅（電圧）の2変数によって表される関数になります。一般に時間を横軸として、振幅（電圧）を縦軸として次のようなグラフで書かれたりします。世の中でよく見る音声の波形と呼ばれるやつはこれです。

※縦軸の振幅は正規化された値とすることが多いので、一般的には無単位です。

音を聞く、考えるときに大事な「周波数」

フーリエ変換

上に挙げたような音声の波形を見ても、混沌としていて情報が全く入ってきません。
ここで役に立ってくるのが、あらゆる信号や波動を扱うときに欠かせない「フーリエ変換」です。

さっき出てきた音声の信号を、時間をt、振幅をyとすると、
波形のグラフを表す式（＝信号）は、y = f(t)　と書けますね？

実は、どんな信号　y = f(t)　も、三角関数の　ふがふが * sin(ほげほげ * t)　の和で表すことができます。

このようにして信号を三角関数の和にバラしてあげた時、それぞれの「ほげほげ」と、それがどれくらい強く含まれるのかという「ふがふが」の組み合わせにバラしてしまうのがフーリエ変換でやっていることです。

周期と周波数

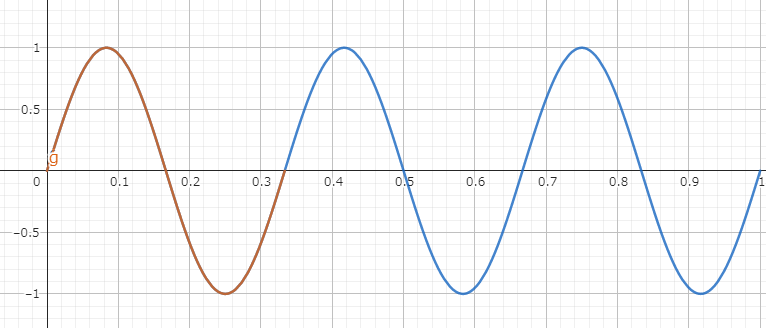
フーリエ変換を上の式で出てきた「ほげほげ」というよくわからない係数で表しても、実世界で使う単位と対応づいていないので意味がよくわかりません。例えば次のような三角関数の足し合わせだとわかりやすいはずです。

横軸を時間(秒)だと思ってください。この図では、1秒間の波形（青色部分）に、赤色部分の形（sinの1周期分）が3回分繰り返されていることがわかります。このように、1秒間に波形の最小単位何回含まれているかを「周波数」と呼び、単位はHz(ヘルツ)を使い、図の場合は3Hzということになります。このグラフは y = sin(6πt) を表しているが、3Hzの周波数成分と呼んだほうがわかりやすいですね。

また、波形の最小単位がどのくらいの時間を占めるかを「周期」と呼び、図の場合は1/3(秒）ですね。
(周波数) × (周期) = 1　がいつでも成り立ちます。

音階の周波数

いろんな周波数成分が複雑に混ざり合った音でも、我々の耳は周波数成分に分解することができ、そこからいろんな情報を得られます。
例えば「ア、イ、ウ、エ、オ」のような発音は周波数成分の比で決まっていて、耳は分解した周波数成分によりこれを聞き分けられます。我々の耳は自然にフーリエ変換のようなことを行っているというわけです。

音の高さに関しては、最も強い周波数の成分がそれを決定していると考えられ、周波数が大きいほど音が高くなります。

音楽の世界で扱う音階について考えると、音高が1オクターブ高くなると周波数は2倍になる、という大きな特徴があります。

例えば、C5の音は523.3Hz、E5は659.3Hz、G5は784.0Hzというように、それぞれの音に周波数が対応しています。

この3音は実はCコードを構成する3つの音ですが、C5の音の4周期分、E5の音の5周期分、G5の音の6周期分がほとんど同じ時間であり、このように各音が何周期分で重なるかによって和音の雰囲気が変わってきます。不協和音同士は何周期たってもうまく重ならなかったりします。

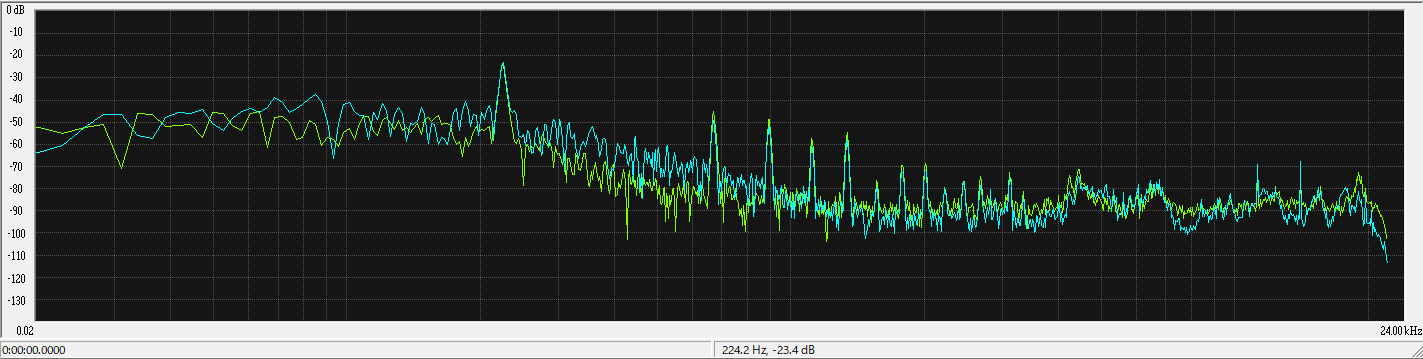
図は、筆者がハミングでA3の音（220.0Hz）の音を出したときにフーリエ変換によって求めた周波数スペクトルです。
真ん中よりちょっと左にピークがありますが、ここは約224Hzで、筆者が出した音の高さにおおむね対応する周波数成分が強く出ていることがわかります。

音声信号をデータとして扱う

音声信号のデジタル化

先述の図の通り、音声信号は「振幅（電圧）の時間に関する関数」で表せる連続（=アナログ）な信号です。
連続なデータをコンピュータで扱うには、無限のメモリが必要になり、不可能です。

Unityでゲーム開発するときに、60fpsで処理を行い約0.016秒ごとの状態だけを再現すれば問題ないように、音声も連続信号のうち一定時間ごとのデータのみを記録すれば元のものに近いものは再現できるはずです。

このような考え方をもとに、実際に一定時間間隔ごとに振幅のデータ列を記録したものが、PCM音源　と呼ばれるものです。
また、この「一定時間間隔ごとにデータを記録する」ことを　サンプリング　あるいは　標本化　と呼びます。
Unity開発でもたまに使うことのあるWAVE形式（.wav）の音声ファイルにはこの形式のデータが入っています。

サンプリング

では、実際に連続な音声信号をサンプリングした時や、サンプリングしたデータをもとに音声を再生するときのことを考えてみましょう。

ナイキスト周波数について

※ここはやや難解なので興味のある方だけどうぞ。説明はかなり噛み砕いていて厳密性に欠けていますがお許しを。

サンプリングされた音声データを実際再生する場合、アナログ信号に変換する必要があるので、サンプル点同士の間は補間してあげる必要があります。ゲーム開発で例えると、10fpsで記録されたアニメーションのカーブをLerp()などで60fpsに補間してあげるのに近いイメージです。ゲーム開発でアニメーションが自然に見えるように補間に使う関数選択するように、音声の場合も数学によって裏付けられた方法で補間します。

上の章で述べたとおり、音を聞いたりするときには含まれる周波数成分で考えるのが大事です。
「人の耳が聞こえる音の周波数成分には上限、下限がある」が通説なので、例えば「音声信号のある周波数を下回る周波数成分は完全に再現でき、上回る周波数成分は切り捨てても良い」ような補間の方法があれば人の耳がごまかせて完璧そうに見えます。都合のいいことに実際に可能です。

音声信号に対して、サンプリング周波数 * 1/2 以下の周波数成分は完全に再現でき、これを超える周波数成分はうまく再現できません。
これを サンプリング定理 と言い、この定理を予想したナイキストさんの名にちなんで、サンプリング周波数 * 1/2のことを ナイキスト周波数 と言います。

※なぜ、ナイキスト周波数を超える周波数成分を再現できないのかについては、以下の記事の図示がわかりやすいので気になる方は見てみてください。
https://kinokorori.hatenablog.com/entry/20161207/1481117395

Unityで実装する

さて、いよいよ本題のピッチ推定の実装を行います。
数種類の方法で実装するので、扱いやすいようにピッチの取得方法を共通化する簡易的なインターフェイスを定義しておきます。

IPitchDetection

public interface IPitchDetection
{
    // 音声入力があるか
    bool IsSoundDetected { get; }
    // 現在のピッチをヘルツで取得する
    float CurrentHertz { get; }
}

定番のFFT (高速フーリエ変換)

ピッチを推定するのですから、もちろんフーリエ変換を行って各周波数成分を見るのが正攻法です。
FFT（高速フーリエ変換）というアルゴリズムが、離散信号を解析するときにもっとも一般的に使われるアルゴリズムで、こちらはUnity標準の機能で利用できます。
アルゴリズムについては以下の記事が詳しいので、興味のある方はご覧ください。
https://qiita.com/ageprocpp/items/0d63d4ed80de4a35fe79

準備

まずは、Editorで設定してもらう項目群や、マイクの取得回りを実装します。
マイクの初期化はイベント関数 Start() でやります。

準備

public class PitchDetectFFT : MonoBehaviour,IPitchDetection
{
    private AudioSource audioSource;

    [SerializeField]
    private int SamplingRate = 12000; // サンプリング周波数

    private bool isSoundDetected = false;
    private float currentHertz = 0;

    public bool IsSoundDetected => isSoundDetected;
    public float CurrentHertz => currentHertz;

    void Start()
    {
        // マイクを扱う
        if (Microphone.devices.Length == 0) return;

        audioSource = GetComponent<AudioSource>();
        audioSource.loop = true;

        // OSデフォルトのマイクデバイスは、Microphone.devices[0]に格納されている。
        audioSource.clip = Microphone.Start(Microphone.devices[0], true, 1, SamplingRate);
        audioSource.Play();
    }
}

FFTの結果を得る

上でも述べたように、Unityでは、標準の機能を用いてFFTの結果を得られます。
AudioSource.GetSpectrumData というメソッドです。
AudioSourceの現時点での周波数スペクトル（それぞれの周波数成分の強さ）を取得することができます。

音声バッファが一定のサイズに達するごとにその時点での周波数スペクトルを得て分析することが理想的ですが、このメソッドは残念ながら　現時点の周波数スペクトルを得ることしかできず、さらにその計算に何サンプル分のデータを使っているかはブラックボックス　ですので、厳密に分析するにはちょっと機能不足です。プレイヤーループでそれっぽくやるしかありません。
ただ非常に簡単に扱えるので、その恩恵にあずかってイベント関数 Update() でそれっぽい間隔ごとに取得して実装してしまいましょう。

Update

void Update()
{
    // 第一引数に渡す配列に、周波数スペクトルのデータが格納される。
    // FFTのアルゴリズムの特性上、サイズは2のべき乗（2,4,8...1024...)である必要がある。
    float[] spectrum = new float[2048];
    audioSource.GetSpectrumData(spectrum, 0, FFTWindow.BlackmanHarris);

    // spectrum = new Float[N]の各番地iに格納されるデータspectrum[i]に対応する周波数について
    // spectrum[0]:0Hz, spectrum[N-1]:ナイキスト周波数となっているので、データは、(ナイキスト周波数 / N)Hz 刻みに入っている
       
    // 次に、最も強度の強い周波数成分を求める。まずはデータの番地から
    var max = 0;
    for (int i = 0; i < spectrum.Length; i++)
    {
        var current = spectrum[i];
        if (current > spectrum[max])
        {
            max = i;
        }
    }

    // データのmax番地が最も強度の強い周波数成分である。これを周波数に変換する。
    var nyquistFreq = (float)SamplingRate / 2f;
    currentHertz = nyquistFreq * (max / spectrum.Length);
}

入力の有無を判定する

音声の入力がない（＝非常に弱い）ときにも判定してしまうのはよくないので、IPitchDetectionで定義したIsSoundDetectedもしっかり実装しておきましょう。

CheckIsAudioDetected

private bool CheckIsAudioDetected(){
    // 波形の生データを使います。
    var buffer = new float[1024];
    // ステレオは扱わない前提なので、channelは0に固定
    audioSource.GetOutputData(buffer, 0);
    var total = 0f;
    foreach (var f in buffer)
    {
        total += f * f;
    }

    // averageが音量である。適切な閾値を設定し、それを超えているかどうかで入力の有無を判定する。
    var average = Mathf.Sqrt(total / buffer.Length);
    
    // ここでは閾値を0.01fにしてみる。
    if (average <= 0.01f)
    {
        return false;
    }
    return true;
}

// Update (追加実装)
void Update()
{
    isSoundDetected = CheckIsAudioDetected();
    if(!isSoundDetected) return;

    // 第一引数に渡す配列に、周波数スペクトルのデータが格納される。
    // FFTのアルゴリズムの特性上、サイズは2のべき乗（2,4,8...1024...)である必要がある。
    float[] spectrum = new float[2048];

   

ここまで実装できれば、ピッチを推定できるはずです。お疲れさまでした。

FFTの惜しいところ

以上の実装で、ピッチを推定できるということを書いてきましたが、この手法で困る点がいくつかあるので挙げておきたいと思います。

まず、一つ目としては、割と負荷が高い という点です。
Unityで実装するということは、大抵の場合ゲームなどのリアルタイム性の求められる場面で使うでしょう。
FFTの計算負荷がボトルネックになってしまう場合があると思います。

次に、二つ目として、低周波領域の分解能に難がある という点です。
ピッチ推定では、ほとんどの場合は音階の音名（ドレミ）などに変換すると思います。
上でも述べたように、オクターブが上がるごとに、１オクターブが占める周波数の領域は２倍ずつ増えていきます。
つまり、高いオクターブでは隣接する音同士の周波数はかなり離れているのに対して、低いオクターブでは、音同士の周波数がほとんど離れていない状態です。
サンプリング周波数12000Hzに対して、フレームサイズ1024でFFTする場合を考えてみましょう。
得られる周波数スペクトルの隣接する周波数の差は ナイキスト周波数/フレームサイズ = 11.7Hz です。
一方、人の声に含まれる C3の音は130.8Hz ,C#3は138.6Hz とその差は 7.8Hz しかありません。
この二つの音を判定するのはフレームサイズ1024のFFTではかなり困難です。
フレームサイズ1024でもかなり大きめなので、これを大きくすれば負荷が上がってしまいますし、実際には隣り合う音よりもっと細かく判定したい場合も多くてこの分解能では問題です。

波形をもとに、周期から攻める

単一周波数成分しかない音声波形は、それを1周期ずらした波形と全く同じ形になりますよね？
（例えば、2Hzの波形は、周期が0.5秒なので、0秒から見た波形と、0.5秒前から見た波形は同じになるはず）

単一周波数ではないとしても、おおむねある高さの音を発している波形であれば、その音の周波数成分が大きく影響しているはずですから、対応する周期だけずらした波形と元の波形は、似た形になることは想像できると思います。

波形が似ているかどうかについて、実はいくつかの関数・アルゴリズムで判定することができるので、ピッチを知りたい音声波形に対して、いろんな量をずらしてみたときの波形とどのくらい位似ているかを判定する ことで、その波形の周期に近いものがわかるはずです。
この周期がわかれば、対応する周波数もわかり、音の高さが推定できるはずですね？

ACF(自己相関関数)

二つの波形（連続）もしくはデータ群（離散）がどのくらい似ているかを評価する関数はしばしば相互相関関数などと呼ばれ、上で述べたような自分の波形の周期を判定に使う場合特に自己相関関数と呼ぶ。

ここは結構難しい部分ですが、次に挙げる資料が特にわかりやすいので参考にどうぞ：
http://www.sanko-shoko.net/note.php?id=f7j3
https://ryukau.github.io/filter_notes/pitch_estimation/pitch_estimation.html
https://marui.hatenablog.com/entry/2021/12/25/070000

AMDF

ここまで散々自己相関関数について紹介してきましたが、統計学的にガチガチに固めてある元祖自己相関関数では、分散などで2乗の計算を多くする必要があり、そんなに高速ではありません。（しまいにはFFTを利用した高速化アルゴリズムがあるくらいで、FFTから逃げてきた我々には本末転倒ですね）

ここではやや雑な AMDF(Average Magnitude Deference Function) という関数を使っていきます。

やることは簡単で、ずらす前の関数値と、対応するずらした後の関数値の差の絶対値を足していって、その平均をとる という考えです。
SAD (Sum of Absolute Difference) の平均をとる感じです。（データ数が同じなら別に平均をとらなくてもいいです）

AMDFの実装

では、実際に実装していきましょう。まずは下準備からです。
どの範囲の周波数を調べるのか、Editorで設定できるように [SerializeField] にします。
イベント関数 Start() では、必要なデータサイズなどを計算していきます。

AMDF下準備

public class PitchDetectAMDF : MonoBehaviour,IPitchDetection
{
    private AudioSource audioSource;

    [SerializeField]
    private int MinimumFrequency = 25;

    [SerializeField]
    private int MaxFrequency = 2400;

    [SerializeField]
    private int SamplingRate = 12000;

    private bool isSoundDetected = false;
    private float currentHertz = 0;

    public bool IsSoundDetected => isSoundDetected;
    public float CurrentHertz => currentHertz;

    private uint requiredSize;
    private uint sizeMax;
    private uint sizeMinimum;

    void Start()
    {
        
        // 最小周波数を調べるために必要なサンプル数を計算する。
        double samplesRequired = (double) 2 * SamplingRate / MinimumFrequency;
        requiredSize = (uint) Math.Ceiling(samplesRequired);
        
        // 最小周波数を調べる時の使うサンプル数
        double samplesMax = (double) SamplingRate / MinimumFrequency;
        sizeMax = (uint) Math.Ceiling(samplesMax);

        // 最大周波数を調べる時の使うサンプル数
        double samplesMinimum = (double) SamplingRate / MaxFrequency;
        sizeMinimum = (uint) Math.Ceiling(samplesMinimum);

        AudioSettings.outputSampleRate = SamplingRate;

        if (Microphone.devices.Length == 0) return;

        audioSource = GetComponent<AudioSource>();
        audioSource.loop = true;
        audioSource.clip = Microphone.Start(Microphone.devices[0], true, 1, SamplingRate);

        audioSource.Play();
    }
}

続いて、音声データの扱いについて書いていきます。FFTの時は、やむを得ずプレイヤーループで書いていましたが、こちらでは、きちんとオーディオバッファが埋まるごとに処理を書いていきます。

Unityには OnAudioFilterRead というイベント関数があり、音声バッファーにデータが到着するごとに呼ばれます。このコールバックが呼ばれるのはオーディオ処理用のスレッドであり、ここに処理を書いていけば、メインスレッドをブロックすることはありません。ただ当然UnityのAPIを呼ぶと怒られるので気を付けましょう。

音声バッファーの処理

    void OnAudioFilterRead(float[] data, int channels)
    {
        // ステレオなどのマルチチャンネルの場合、データはチャンネルごとに交互に入っている。
        // 今回では先頭のチャンネルのデータのみを扱いたいので、それをnewBufferに取り出す。
        var newBuffer = new float[data.Length / channels];
        for (int i = 0; i < newBuffer.Length; i++)
        {
            newBuffer[i] = data[i * channels];
        }

        // 貯めているバッファに連結する。Linq使うと遅いかもしれないのでパフォーマンスを気にする場合は要注意
        audioBuffer = audioBuffer.Concat(newBuffer).ToArray();
        
        // 周期を判定するのに必要なデータサイズ（requiredSize）よりも多くのデータがバッファーにたまったら処理をはじめる
        while (audioBuffer.Length >= requiredSize)
        {
            var nextBuffer = audioBuffer.Take((int)requiredSize).ToArray();

            // 音量を判定する
            var total = 0f;
            foreach (var f in newBuffer)
            {
                total += f * f;
            }

            var average = Mathf.Sqrt(total / newBuffer.Length);
            
            if (average <= 0.01f)
            {
                // 入力が弱すぎる
                currentHertz = 0;
                isSoundDetected = false;
            }
            else
            {
                // AMDFで周波数を判定する
                currentHertz = GetHertzByAMDF(nextBuffer);
                isSoundDetected = true;
                
            }

            // 判定に使った部分のバッファーを削除する
            audioBuffer = audioBuffer.Skip((int) requiredSize).ToArray();
        }
        // 出力をミュートする
        for (int i = 0; i < data.Length; i++) {
            data[i] = 0;
        }
    }

では次に、実際にAMDFの部分を実装していきましょう。

AMDF（最低限）

    float GetHertzByAMDF(float[] data)
    {
        // dataの0からxまでを、iからx+ iの対応する値で考える
        // ずらし幅は、sizeMinimumから、sizeMaxの間である

        var result = new float[sizeMax];
        
        // AMDF値を計算する部分
        for (uint i = sizeMinimum; i < sizeMax; i++)
        {
            result[i] = 0;
            //対象データの0からi-1を、iから2i-1までと比較する。
            for (int j = 0; j < sizeMax; j++)
            {
                result[i] += Math.Abs( (data[j] - data[j + i]) / i);
            }
        }

        // AMDF値のボトム（極小）を探す
        // AMDF値が減少から増加に増える瞬間を探してあげる。
        // ボトムのなかでも特に値が小さくなったものが答えである可能性が高いのでそれを返す。

        int bottom = 0;
        
        for (int i = (int)sizeMinimum; i < result.Length - 1; i++)
        {
            if ( result[i] < result[i - 1] && result[i] < result[i + 1])
            {
                if (bottom == 0 || result[i] < result[bottom])
                {
                    bottom = i;
                }
            }
        }

        return SamplingRate / bottom;
    }

ここまでの実装はAMDFの基本に忠実で、最低限ピッチを推定できるはずです。お疲れさまでした。

AMDFの実装をやや改善する

がしかし、このレベルの実装だととても実用に耐えません。次のような問題が起きるからです。

① 正しい周波数の 1/2, 1/3, 1/N の周波数を答えとして誤って選びがちである
周期がt秒の関数をずらす場合、1周期分のt秒のほか、2t秒,3t秒ずらした場合もAMDF値が小さくなります。
誤って、2t,3tに該当する周波数を選んでしまう可能性がありますね。これを回避するためには、「できるだけ周波数の高いもを選ぶ」　などのアルゴリズムが必要そうです。

② 短い周期（＝高い周波数）の分解能が悪い
FFTの場合とは逆に、ずらす大きさが小さい高周波数の推定で、分解能が悪くなってしまいます。
例えばサンプリング周波数9000Hzの場合、9サンプルずらし(1000Hz)と10サンプルずらし(900Hz)では100Hzも差が出てしまうが、50サンプルずらし(180Hz)と51サンプルずらし(176.47Hz)では4Hz程度しか差が出ない。

高周波域ではそもそも1音あたりの周波数差がかなり大きいので、これはあまり問題になりませんが、対策できるならしておきたいですね。
「①の問題を逆に利用して2t秒,3t秒ずらした場合の周波数から逆算する」「二次関数によって間の値を補間する」などのアルゴリズムで対応できそうです。

今回は、太字で示した部分のアルゴリズムを実際に実装していきます。

AMDF

    float GetHertzByAMDF(float[] data)
    {
        // dataの0からxまでを、iからx+ iの対応する値で考える
        // ずらし幅は、sizeMinimumから、sizeMaxの間である

        var result = new float[sizeMax];
        
        for (uint i = sizeMinimum; i < sizeMax; i++)
        {
            result[i] = 0;
            //対象データの0からi-1を、iから2i-1までと比較する。
            for (int j = 0; j < sizeMax; j++)
            {
                result[i] += Math.Abs( (data[j] - data[j + i]) / i);
            }
        }
        
        // ボトムの番地を全部記録しておくためのリスト
        var possibility = new List<int>();

        int bottom = 0;
        
        for (int i = (int)sizeMinimum; i < result.Length - 1; i++)
        {
            if ( result[i] < result[i - 1] && result[i] < result[i + 1])
            {
                // 番地
                possibility.Add(i);
                
                if (bottom == 0 || result[i] < result[bottom])
                {
                    bottom = i;
                }
            }
        }

        var lastIndex = bottom;
        // 全ボトムの番地に対して調べる
        foreach (var i in possibility)
        {
            // 暫定の答えのボトム値
            var leastValue = result[bottom];

            // 周波数が高いものを無条件に選ぶわけにはいかないので、周波数が高くかつ最小値の1.1倍を閾値とし、それより小さいものを選ぶ
            if (result[i] < leastValue * 1.1f && i < lastIndex)
            {
                lastIndex = i;
            }
        }
        
        if (lastIndex <= 1) return 0;


        // ここから先は、高周波の分解能が悪い問題に対処する
        float accurateIndex = (float)lastIndex;
        
        // lastIndexが求める周期だとすると、lastIndex - 1 から lastIndex + 1　の間に対応する周期が答えになる可能性がある。
        // (lastIndex + 1)を整数Ｎ倍した値が最大であるsizeMaxを超えない範囲で周期がＮ倍になっているピークがあれば、それを探してからＮ分の１すれば、
        // より精度の高い周波数を得ることができる。

        var currentRatio = (int)Math.Floor((float)sizeMax / (lastIndex - 1));

        // 8倍の周期までを調べる。大きくなりすぎてしまうと違う値を持ってきうる
        if (currentRatio > 8) currentRatio = 8;

        while (currentRatio > 1)
        {

            var min = (lastIndex - 1) * currentRatio;
            var compare = lastIndex * currentRatio;
            var max = (lastIndex + 1) * currentRatio;
            
            var values = possibility.Where(x => (min < x) && (x < max)).ToList();

            int answer = 0; 
            foreach (var value in values)
            {
                if (Math.Abs(value - compare) < Math.Abs(answer - compare))
                {
                    answer = value;
                }
            }

            if (answer != 0)
            {
                accurateIndex = answer / currentRatio;
                break;
            }
            
            currentRatio--;
        }
        return SamplingRate / accurateIndex;
    }

お疲れさまでした！！
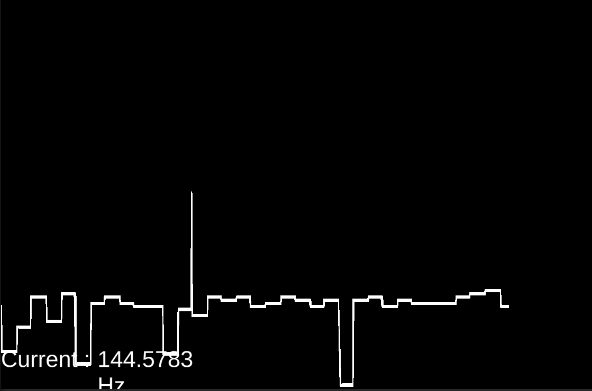
ここまで実装すると、リアルタイム性もあり、制度もそんなに悪くないピッチ推定ができます。

周波数の画面表示と、ピアノロール（とは程遠いが）風のグラフをLineRendererで書いてみたものが上の図です。

AMDFで今回できなかったこと、やっておきたいこと

ピッチ推定というごくシンプルなことをやっているのに、まだまだ課題はたくさんあります。本当は今回やりたかったんですが、進捗が悪く書ききれなかった問題を挙げておきます。またどこかの機会で...

① 時間に正確ではない
今回は、OnAudioFilterRead内で実装をして、それをどこかのComponentがUpdateなどからピッチを読むという実装になっているが、これでは時間が正確になりません。OnAudioFilterReadが呼ばれた時点でタイムスタンプを記録し、AMDF値の計算が終わった時点で値をタイムスタンプと紐づける、というような実装が必要です。 今回の実装ではこれができておらず、「AMDFの計算負荷によって経過した時間」「OnAudioFilterReadの実行完了から次のプレイヤーループ関数が呼ばれるまでの時間」という不確定な時間が加算されています。
連続的にピッチを推定するには、どのタイミングのデータからどのピッチが得られたかという絶対的な時間の結び付けが必要です。

ピッチと時間をセットにした構造体を、UniRxのReactivePropertyあたりで公開してあげれば、扱いやすいのではないかととりあえず妄想の中ではまとまっています...

② 飛び値を排除できていない

今回の実装では、ある瞬間の値を使っているので、飛び値が発生してしまうことがどうしてもあります。ピッチは一定時間においては定常的なはずなので、飛び値であるかどうかは計算でき、排除可能です。「一定時間内に複数回ピッチ推定を行い、安定した値を算出する」アルゴリズムが必要です。時間を使うので、まずは、①を実装しないといけないですね...

③ AMDF値に利用するデータが固定長になっている
AMDF値を計算するとき、周期の短い（と仮定できる）波形は少ないデータ量、周期の長い（と仮定できる）波形は多いデータ量というように、使うデータ長を可変にすることができそうです。これを行うことでより処理負荷を抑えたり、周期の短い（と仮定できる）波形のピッチ推定頻度を上げたりという最適化が可能です。

感想

Unityでピッチ推定を行う方法として、簡易的なものから割と痒い所まで手が届くものとして、Unityが提供するFFTと、自分で一から実装するAMDFを紹介してみました。Unityで音声を扱う際にためになったら嬉しいなと思いますし、読んでくださった方にぜひピッチで遊ぶようなゲームを実装していただければと考えています。（僕が個人的にそういうゲームが大好きなだけですが）

ノリで参加してみたアドベントカレンダーではあったが、そもそも今回がQiitaでの初投稿ということもあり、書くのにかかる時間をかなり見積り誤りました。本当はCQT(Constant-Q変換)などもやってみたかったのですが、全然間に合わなかったので、またの機会に書きたいと思います。

※バグや質問等ありましたらコメントまたはTwitterにお気軽にご連絡ください。