を読みました。興味深かったので、実際にこれを用いてオンラインカジノに100ドル入れてモンテカルロ法を実践してみてるんですけど現在+35ドルくらい稼げていてすごいなあと思いました。
しかし、その中で一度やばいパターンを引いたりして所持額が0になりかけたりもしてやばかったこともあり、「これって実際の状況だと本当に稼げるの...?」と思い、実際の状況を想定したシミュレーションをしました。
前提
- スタート時の金額は1000ドル
- 1単位を1ドルとする。
- 所持金がn倍になるor0未満になるまで実行をし、その一連の動作を1000回行い、勝率を計算する。
- ルーレットにおける2倍モンテカルロ法、3倍モンテカルロ法どちらも行う。
- 2倍時の1回の勝率は18/37(0~36のうちの0を除いた18通り)、3倍時の1回の勝率は12/37(同様)とする。
(復習)モンテカルロ法って?
①初期配列として以下の配列を用意する
[1, 2, 3]
②配列の最初の値と最後の値を足したものをベットする
ベット額:4
③負けた場合、ベット額を配列の最後に追加する
[1, 2, 3, 4]
④勝った場合、2倍モンテカルロ法なら配列の最初の値と最後の値、3倍モンテカルロ法なら最初2つの値と最後2つの値を配列から消す
2倍:[2, 3]
3倍:[]
⑤②〜④を繰り返し配列の長さが2未満になったら終了。①に戻る
簡単でしょう?
2倍モンテカルロ法
ソースコード
import random
win = 0
max_win = 0
max_bet = 0
n = float(input("n = "))
goal = 1000 * n
def kake(money, monte, max_bet):
bet_gaku = monte[0] + monte[-1]
max_bet = max(max_bet, bet_gaku)
money -= bet_gaku
n = random.randint(0, 36)
if(n > 18):
money += bet_gaku*2
monte.pop(0)
monte.pop(-1)
else:
monte.append(bet_gaku)
lose_count += 1
return money, monte, max_bet
for _ in range(1000):
monte = [1, 2, 3]
money = 1000
while(0 < money < goal):
money, monte, max_bet = kake(money, monte, max_bet)
if(len(monte) < 2):
monte = [1, 2, 3]
if(money > 0):
max_win = max(max_win, money)
win += 1
print("max_win:" + str(max_win))
print("max_bet:" + str(max_bet))
print("rate:" + str(win/1000))
n = 1.1〜2.0, 3, 4, 5, 10についてまとめました。
結果
| n | 勝率(%) | 最大の勝ち | 1回の最大の賭け額 |
|---|---|---|---|
| 1.1 | 87.2 | 1105 | 517 |
| 1.2 | 77.2 | 1205 | 704 |
| 1.3 | 66.4 | 1305 | 724 |
| 1.4 | 59.0 | 1405 | 798 |
| 1.5 | 55.0 | 1505 | 935 |
| 1.6 | 47.5 | 1605 | 1050 |
| 1.7 | 45.5 | 1705 | 852 |
| 1.8 | 41.4 | 1805 | 859 |
| 1.9 | 38.1 | 1905 | 979 |
| 2.0 | 34.1 | 2005 | 944 |
| 3.0 | 16.5 | 3005 | 1352 |
| 4.0 | 8.9 | 4005 | 1836 |
| 5.0 | 6.4 | 5005 | 2679 |
| 10.0 | 1.5 | 10005 | 4080 |
いかがでしたか?(糞ブログ感)1.6倍にする少し手前で勝率は5割を切ってしまうということがわかります。また、1回に賭ける額に関しても、+100ドル増やすだけでも517ドル賭けるタイミングが訪れる可能性があるという結果になりました。
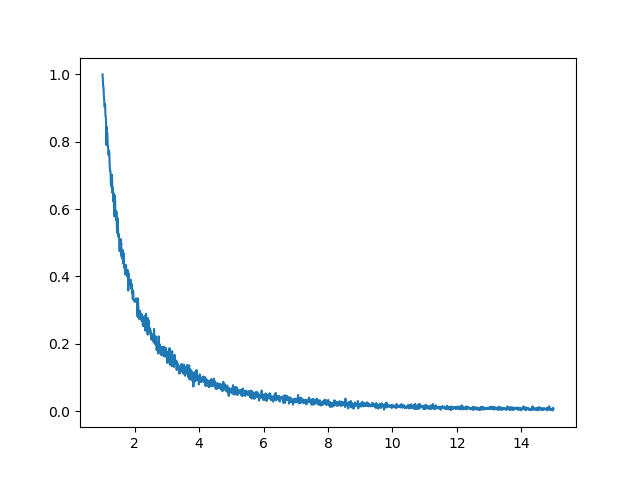
参考までにn = 1 〜 20までプロットしたものを載せておきます。
若干のブレはありますがきれいなカーブを描いています。まあ間違いなくやらないほうがいいですね...。
3倍モンテカルロ法
ソースコード
from matplotlib import pyplot
import random
nn = [1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2, 3, 4, 5, 10]
rate_all = []
win_all = []
bet_all = []
def kake(money, monte, max_kake):
kake_gaku = monte[0] + monte[-1]
max_kake = max(max_kake, kake_gaku)
money -= kake_gaku
n = random.randint(0, 36)
if(n > 23):
money += kake_gaku*3
if(len(monte) >= 4):
monte.pop(0)
monte.pop(0)
monte.pop(-1)
monte.pop(-1)
else:
monte = [1, 2, 3]
else:
monte.append(kake_gaku)
return money, monte, max_kake
for n in nn:
win = 0
max_win = 0
max_kake = 0
goal = 1000 * n
for _ in range(1000):
monte = [1, 2, 3]
money = 1000
while(0 < money < goal):
money, monte, max_kake = kake(money, monte, max_kake)
if(len(monte) < 3):
monte = [1, 2, 3]
if(money > 0):
max_win = max(max_win, money)
win += 1
rate_all.append(win / 1000)
win_all.append(max_win)
bet_all.append(max_kake)
# pyplot.plot(nn, rate_all)
# pyplot.show()
print(rate_all)
print(win_all)
print(bet_all)
結果
| n | 勝率(%) | 最大の勝ち | 1回の最大の賭け額 |
|---|---|---|---|
| 1.1 | 95.7 | 1343 | 395 |
| 1.2 | 90.6 | 1379 | 420 |
| 1.3 | 86.7 | 1461 | 478 |
| 1.4 | 83.8 | 1636 | 501 |
| 1.5 | 82.9 | 1706 | 652 |
| 1.6 | 81.5 | 1936 | 618 |
| 1.7 | 78.9 | 1903 | 600 |
| 1.8 | 74.3 | 2038 | 633 |
| 1.9 | 73.8 | 2204 | 728 |
| 2.0 | 70.1 | 2203 | 770 |
| 3.0 | 61.9 | 3520 | 1098 |
| 4.0 | 54.7 | 4531 | 1463 |
| 5.0 | 48.9 | 5942 | 1486 |
| 10.0 | 38.9 | 10931 | 3537 |
2倍のときとは段違いに勝ててしまう、正直めちゃくちゃ意外な結果になりました。ゲームごとの勝率よりも大局的に見た時の数列の減りやすさの方が優先されるってことなんですかね。
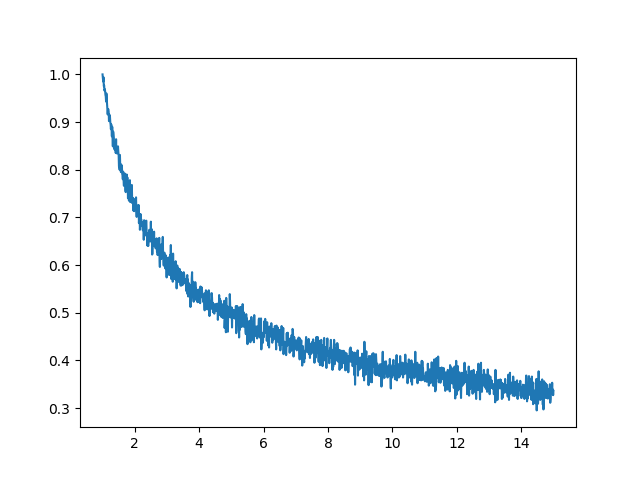
これもプロットしてみました。
さっきと形こそ似てしまってますがグラフの下限値が全然違いますね。5倍程度に増やしたいなら勝率5割もあることがわかり、15倍でも3割ほどは」勝ててしまうことが実証されました。
ちなみにこのあとn=100, 1000で試したのですが、18.9%、12.7%という結果が出ました。元手1000ドルから始めているわけですから8人に1人くらいはミリオネアが誕生してしまう、ロマンの塊ですね...!
稼ぎたいなら3倍モンテカルロ法をやれ!!
はい、当然結論としてはこういうことになります。モンテカルロ法のルールに従うと、数字の配列の量を減らしていくことに成るのですが、2倍、3倍それぞれの1度に減らすことのできる量の期待値は以下のとおりになります。
2倍:
\frac{18}{37} * 2 - \frac{19}{37} = \frac{17}{37}
3倍:
\frac{12}{37} * 4 - \frac{25}{37} = \frac{23}{37}
やはり期待値の大きい3倍の方が配列の減少ペースも早く、あまり高額ベットをする必要がなく勝てるということなのですかね...逆に2倍モンテカルロ法については期待値的には勝てるはずなのに2倍に増やすことすら難しいというのは正直予想外でした。
という感じでここまで書いていきましたが何か訂正箇所等ありましたら質問お願いします。