はじめに
白雪巴さんが「世界のアソビ大全51」配信にて「ヨット」をプレイしていた時のこと.
「ここでチョイスはもったいない」
と言っていました.(その時の得点は20)
ふと疑問に思ったので, 少し調べてみました.
ヨットとは5つのサイコロを振って手を作るゲームであり, チョイスはその中の手の一つです.
チョイスは, すべての目の合計が得点となる役です.
結論
20はチョイス選択「あり」
- チョイスの平均は17.5
- 20未満になる確率は 69.48%
- 21以上になる確率は 22.14%
前準備
1~6までの目がある1個のさいころを投げるとき, 出る目の数字の平均を考えます.
(※目の出方は同様に確からしいものとする)
ここで, さいころの目の合計は 21であり, それぞれの目は均等に出ることが期待できるため, もとめる平均 $E(x)$ は
$$
E(x) = \frac{1}{6} \times 21 = \frac{7}{2}
$$
と計算することが出来ます.
このように求めた$E(x)$ のことを $X$ の期待値と呼び
$$
\begin{eqnarray}
E(x)
&=& x_1p_1 + x_2p_2 + \cdots + x_np_n \
&=& \sum^n_{k=1}x_kp_k\
&&(X = x_1, x_2, ..., x_n)(P=p_1, p_2, ..., p_n)
\end{eqnarray}
$$
としてもとめられる.
本題
では, さいころを同時に5個投げた場合, 出た目の合計の平均を考えます.
このとき, 5個のさいころに対する確率は独立しているため, 単純に足し合わせれば求める平均を得ることが出来ます.
つまり
$$
E(x) = \frac{7}{2} \times 5 = \frac{35}{2}
$$
となります.
$X$ を確率変数, $a$, $b$ を定数とするとき
$$
E(aX+b) = aE(x)+b
$$
が成り立つため, $E(X) = \frac{7}{2}$ , $a=5$, $b=0$ を代入すればもとまる
実践
ここまでは数学を用いて, チョイスの平均をもとめました.
とはいえもうかなり忘れているので, 正しいかどうかわからない...
ここからは Python をもちいて, もとめた平均が正しいか検証します.
なお, 以下のコードはすべて Google Colab にて動作確認しました.
平均計算
戦略は,単純.
1億回 5個のさいころを振り, その目の合計をもとめます. 次に, その平均を求めれば, もとめる平均が求まります.
つまり, 大数の法則です.
実際に試したコードが以下になります.
import numpy as np
# 試行回数
N = 1 * 10**8
# チョイス実行
x = np.random.randint(1, 6+1, (N, 5))
x = x.sum(axis=1)
# 平均計算
print(np.mean(x))
# 17.4996012
結果は 17.4996012 となり, 計算結果とほぼ一致していました.
簡単に解説をば.
7行目にて, 1~6の乱数を サイズ(N, 5) で作成します.
8行目にて, 5個のさいころの合計をそれぞれ計算します.
ヒストグラム
思ったほか簡単に試せたので, おまけでヒストグラムを作成してみました.
実際に使ったコードが以下になります.
import numpy as np
import matplotlib.pyplot as plt
# 試行回数
N = 1 * 10**8
# チョイス実行
x = np.random.randint(1, 6+1, (N, 5))
x = x.sum(axis=1)
# ヒストグラム生成
result = plt.hist(x, bins=26, alpha=0.5, color=(0.43, 0.25, 0.91))
# 補助線
ex = 17.5
min_ylim, max_ylim = plt.ylim()
plt.axvline(17.5, color='k', linestyle='dashed', linewidth=1)
plt.text(ex*1.05, max_ylim*0.9, f"E(x)={ex}")
plt.axvline(20, color='w', linestyle='dashed', linewidth=1)
# ラベル
plt.title('Distribution of Scores in "Choice"')
plt.xlabel("point")
plt.ylabel("frequency")
plt.savefig("fig.png")
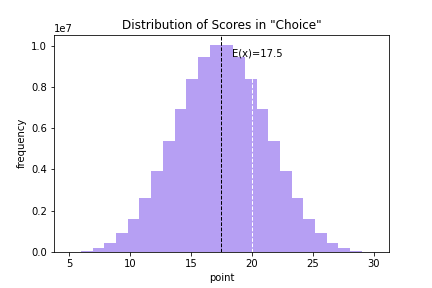
これにて出来たヒストグラムが以下になります.
このヒストグラムにおいて, 黒の点線が平均, 白の点線が20 となっています.
これより, 平均より超えていることが一目でわかるようになりました.
20未満の確率
さて, チョイスの得点が20未満になる確率はどれぐらいでしょうか?
これが分かれば, 説得力が増えそうです.
というわけで, Python にお願いして, 近似的に求めてみます.
import numpy as np
# 試行回数
N = 1 * 10**8
# チョイス実行
x = np.random.randint(1, 6+1, (N, 5))
x = x.sum(axis=1)
# 頻度計算
uni, counts = np.unique(x, return_counts=True)
d = {str(u): c for u, c in zip(uni, counts)}
# 20未満の発生確率
temp = [v for k, v in d.items() if int(k) < 20]
print(f"{(sum(temp) / N)*100:.02f}%")
# 69.48%
結果は 69.48% となり, 全体の約7割が20未満となることが分かりました.
また, このプログラム 15行目にある不等号の向きを変えれば, 簡単に21以上の発生確率も調べることが出来ます.
結果は 22.14% つまり, これ以上高い手になる確率は 約2割となります.
ソシャゲのガチャに毒されているので高く感じますが... といった感じです.
おわりに
アソビ大全のゲーム 解析してみる楽しい