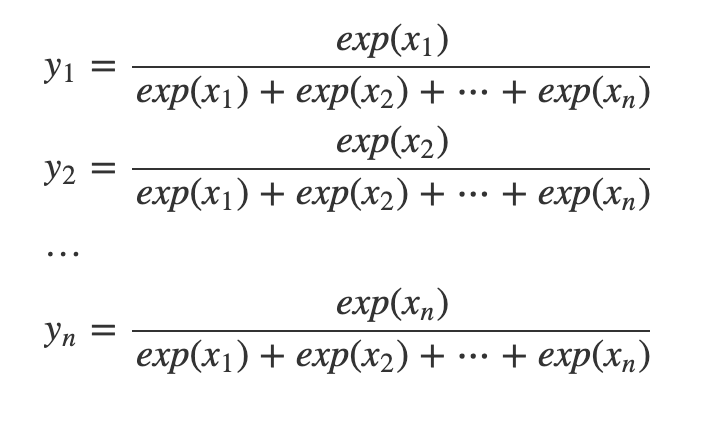p.42 活性化関数の登場
式(3.3)はステップ関数に等しく、$x = b + w_{1}x_{1} + w_{2}x_{2}$
p.45 シグモイド関数
$y = f(x) = e^x$ の傾き $f'(0) = 1$
p.58 行列を使ったニューラルネットワーク
\begin{pmatrix} x_{1} & x_{2}\end{pmatrix} \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{pmatrix}= \begin{pmatrix} x_{1} + 2x_{2} & 3x_{1} + 4x_{2} & 5x_{1} + 6x_{2}\end{pmatrix}
p.61 各層における信号伝達の実装
式(3.9)は図3.14にバイアスを加えたのと同じ
p.61 各層における信号伝達の実装
$Z1$は$z_{1}^{(1)}, z_{2}^{(1)}, z_{3}^{(1)}$を指す
p.69 ソフトマックス関数の実装上の注意
$ exp({logC}) = e^{log_eC}$
$x = logeC$ とすると、この意味は「eをx乗したらC」
よって $e^x = C$ つまり $C = e^{log_eC} = exp({logC})$ となる。
p.70 ソフトマックス関数の特徴
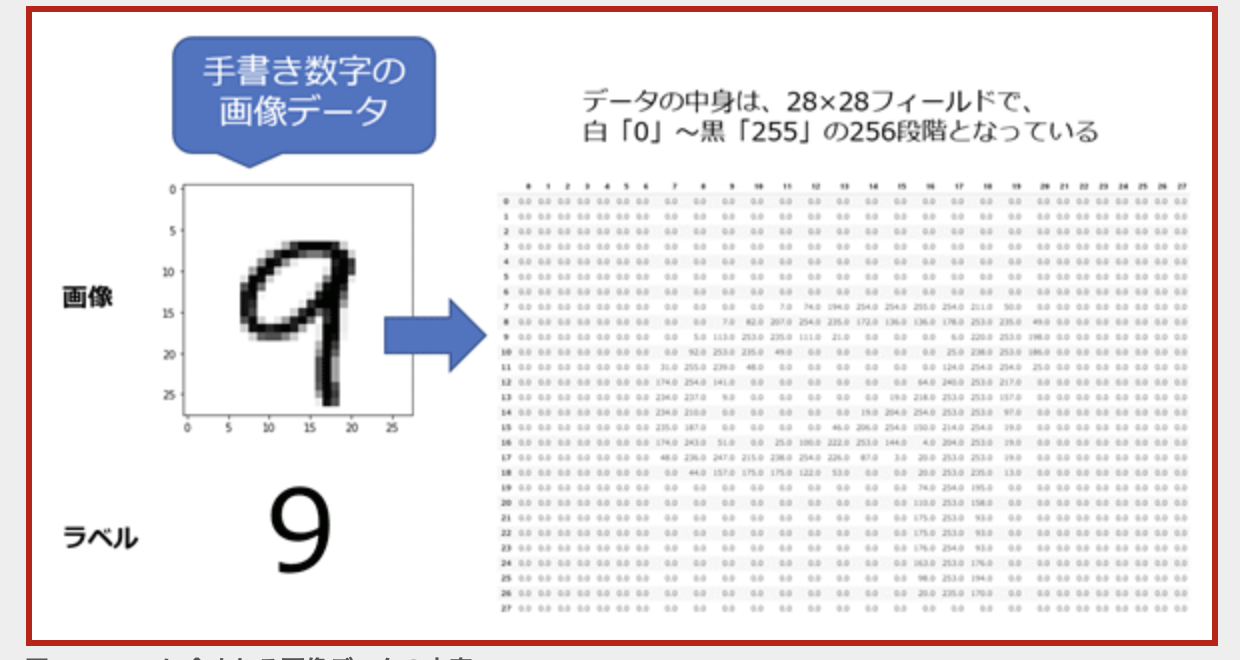
p.72 MNISTデータセット
p.75 ニューラルネットワークの推論処理
predictのWとbは決められたものをロードしているので学習ではなく推論
p.78 バッチ処理
p.93 ミニバッチ学習
x_batch.shape[0] が y.shape[0] になる (図3-27と同じ)
行を引っこ抜いてくる
p.94 [バッチ対応版] 交差エントロピー誤差の実装
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
# y = [
# [o,o,...,o],
# [o,o,...,o],
# [o,o,...,o],
# [o,o,...,o],
# [o,o,...,o]
# ]
# y.shape (5, 10)
# t_batch = [
# [o,o,...,o],
# [o,o,...,o],
# [o,o,...,o],
# [o,o,...,o],
# [o,o,...,o]
# ]
# t_batch.shape (5, 10)
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
# array([[0, 0, 1, 0, 0, 0, 0, 0, 0, 0]])
y = y.reshape(1, y.size)
# array([[0.1 , 0.05, 0.6 , 0. , 0.05, 0.1 , 0.1 , 0.1 , 0. , 0. ]])
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
# y = [o,o,...,o]
# y.shape (10,)
# t_batch = [o,o,...,o]
# t_batch.shape (10,)
>>> t = [0,0,1,0,0,0,0,0,0,0]
>>> y = [0.1,0.05,0.6,0.0,0.05,0.1,0.1,0.1,0.0,0.0]
>>> nt = np.array(t)
>>> nt.shape
(10,)
>>> ny = np.array(y)
>>> ny.shape
(10,)
>>> nt.size
10
>>> ny
array([0.1 , 0.05, 0.6 , 0. , 0.05, 0.1 , 0.1 , 0.1 , 0. , 0. ])
>>> nt
array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
>>> rnt = nt.reshape(1, 10)
>>> rnt
array([[0, 0, 1, 0, 0, 0, 0, 0, 0, 0]])
>>> rny = ny.reshape(1, 10)
>>> rny
array([[0.1 , 0.05, 0.6 , 0. , 0.05, 0.1 , 0.1 , 0.1 , 0. , 0. ]])
>>> -np.sum(rnt * np.log(rny + 1e-7)) / 10
0.0510825457099338
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
# y = [
# [o,o,...,o],
# [o,o,...,o],
# [o,o,...,o],
# [o,o,...,o]
# ]
# y.shape (5, 10)
# t_batch = [
# [o],
# [o],
# [o],
# [o],
# [o]
# ]
# t_batch.shape (5, 1)
yにおけるtを抽出して他は無視する
p.99 微分
hを無限に0へと近づけることができないので1e-50にしている
p.101 数値微分の例
def tangent_line(f, x):
d = numerical_diff(f, x)
print(d)
y = f(x) - d*x
return lambda t: d*t + y
d: 接線の傾き
y: 接線の切片
接線を$p = dq + y$ とすると、 $(x, f(x))$ を通るので 切片$y = f(x) - dx$
lambda t: d*t + y: $f(t) = dt + y$
p.102 偏微分
p.104 勾配
def numerical_gradient(f, x):
h = 1e-4
# [0, 0]
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
# 順番に+h, -hを適用する
x[idx] = tmp_val + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 値を元に戻す
return grad
# def f(x):
# return x[0]**2 + x[1]**2
# x = [3, 4]
# def numerical_diff(f, x):
# h = 1e-4
# return (f(x+h) - f(x-h)) / (2*h)
p.111 ニューラルネットワークに対する勾配
numerical_gradientの引数fつまり損失関数が引数xつまり重みによってどう変化していくか
重み -= 学習率 * 勾配 で更新していき、損失関数の値を小さくしていく
p.123 誤差逆伝播法
p.104では $\left( \dfrac{\partial f}{\partial x_{0},}\dfrac{\partial f}{\partial x_{1}}\right)$ のような勾配を求めた。
図5-7では段階的に微分を乗算し、最終的に $\dfrac{\partial z}{\partial x}$ を求めている。
図5-12では $\dfrac{\partial L}{\partial z} * \dfrac{\partial z}{\partial x}$で最終的に $\dfrac{\partial L}{\partial x}$ を求めるため、$z = xy$ (乗算)の場合、 $\dfrac{\partial z}{\partial x} = y$ となる性質を用いている。
ニューラルネットワークに適用する際は、レイヤが用いられる。
p.142 ReLUレイヤ
# 0以下の要素を抽出
print(x[mask])
# 0以下の要素を0置換
x[mask] = 0
print(x)
p.143 Sigmoidレイヤ
$\dfrac{f\left( x\right) }{g\left( x\right) }$ の微分は、$\dfrac{f'\left( x\right) g\left( x\right) -f\left( x\right) g'\left( x\right) }{g\left( x\right) ^{2}}$
$\lim _{x\rightarrow 0}\left( 1+x\right) ^{\dfrac{1}{x}}=e$
よって $y = e^x$ の微分は無変化。
p.167 SGD
grads: 勾配
勾配を求めるのが微分であり誤差逆伝播法
SDG: optimizer
勾配を使って重みをどのように更新していくか
p.182 隠れ層のアクティベーション分布
p.186 Batch Normalization
if self.use_batchnorm:
self.params['gamma' + str(idx)] = np.ones(hidden_size_list[idx-1])
self.params['beta' + str(idx)] = np.zeros(hidden_size_list[idx-1])
self.layers['BatchNorm' + str(idx)] = BatchNormalization(self.params['gamma' + str(idx)], self.params['beta' + str(idx)])
p.193 Weight decay
def loss(self, x, t):
y = self.predict(x)
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
return self.last_layer.forward(y, t) + weight_decay
p.198 検証データ
訓練データ: パラメータ(重みやバイアス)の学習に利用
検証データ: ハイパーパラメータ(各層のニューロンの数やバッチサイズ、パラメータの更新の際の学習係数やWeigth decayなど)の性能を評価するために利用
テストデータ: 汎化性能をチェックするために、最後に(理想的には一度だけ)利用
p.207 前結合層の問題点
図3-20が全結合の様子で図3-26が形状
p.222 im2colによる展開
p.233 CNNの実装
「パラメータの勾配は、誤差逆伝播法によって求めます。これは、順伝播と逆伝播を続けて行います。それぞれのレイヤで順伝播と逆伝播の機能が正しく実装されているので、ここでは単にそれらを適切な順番で呼ぶだけです。」
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
...
p.247 層を深くすることのモチベーション
図7-5にある通り、フィルター = 重み = パラメータ