$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
1.はじめに
QiskitではUnitary Simulatorを使って量子回路の行列での表現を求めることができます。回転ゲートのように回転角をパラメータとして入る回路は、回転角に具体的な値を与える前の式の形を知りたい場合があります。このような場合には数式処理で見られるようなシンボリックな計算が必要であり、Qiskitだけでは対応できないようです。
手軽にできる方法はないかと思って調べてみたところ、pytketというライブラリを使うとある程度はできることが分かったのでその結果を記します。
2.Qiskitを使って量子回路の行列表現を求める
ここでは例題として、CXゲートについて量子回路の行列の表現を手計算とQiskitで求めてみます。$q_0$ビットがコントロール、$q_1$ビットがターゲットであるCXゲートの行列は以下の式で表すことができます。
$$
CX_{0,1} = \mathbb{I} \otimes \ket{0}\bra{0} + X \otimes \ket{1}\bra{1}
$$
ここで
\mathbb{I} =
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}, \
X = \begin{bmatrix}0 & 1 \\ 1 & 0 \end{bmatrix},
\ket{0}\bra{0} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\begin{bmatrix} 1 & 0 \end{bmatrix} = \begin{bmatrix}1 & 0 \\ 0 & 0 \end{bmatrix}, \\
\ket{1}\bra{1} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}\begin{bmatrix} 0 & 1 \end{bmatrix} = \begin{bmatrix}0 & 0 \\ 0 & 1 \end{bmatrix}
となっていますから、計算を進めると
CX_{0,1} = \left[
\begin{array}{cc|cc}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
\hline
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0
\end{array}
\right]
\ + \
\left[
\begin{array}{cc|cc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
\hline
0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
\end{array}
\right]
= \left[
\begin{array}{cc|cc}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
\hline
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{array}
\right]
となります(計算が分かりやすくなるように行列内に区切りの線を入れています)。
Qiskitで量子回路を表わすユニタリ行列を求めるコードを実行すると同じ結果が得られます。
from qiskit import QuantumCircuit, Aer, assemble
from qiskit.visualization import array_to_latex
qc = QuantumCircuit(2)
qc.cx(0,1)
usim = Aer.get_backend('unitary_simulator')
qobj = assemble(qc)
unitary = usim.run(qobj).result().get_unitary()
array_to_latex(unitary, prefix="\\text{Circuit = }\n")
Circuit = \left[
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{array}
\right]
CXゲートを表わす行列の要素は数値でしたが、例えば、ブロッホ球の$y$軸周りの回転を表わす$R_y(\theta)$ゲートのようにパラメータを含むゲートが回路に含まれる場合には、$\theta$に具体的な値を入れて計算をする必要があり、量子回路を表わす行列の要素はパラメータを含む式で表すことはできません。
このような計算は数式処理で対応することになりますが、手軽にできる方法はないだろうかとStackExchangeの記事([1][2])などを調べてみた結果、pytketというライブラリを使えばある程度できそうだということがわかりました。
3.pytketを使ってみる
(1)pytketについて
pytketは、英国QUANTINUUM社の量子コンピューティングツールキット"tket"と連携するpythonモジュールであり、同社によって開発されたものです([3])。本稿執筆時点のバージョンは1.11.1です。
pytketでは
- Qiskitの量子回路をtketのそれに変換するqiskit_to_tk関数
- 量子回路からユニタリ表現を求めるcircuit_to_symbolic_unitary関数
が提供されています。ここでは、Qiskitで量子回路を定義したのち、これらの関数を使って実際に量子回路の行列での表現を求めてみます。
(2)準備
pytketを使うための準備として、pytketとpytket-qiskitをpipでインストールします。
pip install pytket
pip install pytket-qiskit
なお、QiskitのインストールについてはQiskitのホームページのインストールの手順(https://qiskit.org/documentation/locale/ja_JP/getting_started.html ) を参考にしてください。
(3)行列表現を求めるためのプログラム
前項でCXゲートの行列表現を求めてみましたが、同じことをpytketを使ってやってみると次のとおりです。

Qiskitで量子回路を定義したのち、qiskit_to_tk関数を使ってtketでの回路に変換し、
circuit_to_symbolic_unitary関数を使って行列表現を求めます。
ここでは、Qiskitとtketでは量子ビットの並び順が逆であるため、tketでの回路に変換する前にreverse_bits()を使って並び順を反転させています。
さらに$y$軸周りの回転を表わす$R_y(\theta)$ゲートの場合をやってみます。$q_1$ビットに回転角$\theta_1$の$R_y$ゲートをおきます。

この場合も前項と同様にして、

という結果を得ました。実際に
R_y(\theta) =
\begin{bmatrix}
\cos \frac{\theta}{2} & -\sin \frac{\theta}{2} \\
\sin \frac{\theta}{2} & \cos \frac{\theta}{2}
\end{bmatrix}
ですから、
R_y(\theta) \otimes \mathbb{I} \ =
\left[
\begin{array}{cccc}
\cos \frac{\theta}{2} & 0 & -\sin \frac{\theta}{2} & 0 \\
0 & \cos \frac{\theta}{2} & 0 & -\sin \frac{\theta}{2} \\
\sin \frac{\theta}{2} & 0 & \cos \frac{\theta}{2} & 0 \\
0 & \sin \frac{\theta}{2} & 0 & \cos \frac{\theta}{2}
\end{array}
\right]
となるので、手計算とpytketでの計算結果は一致しています。
これに加えてCZゲートと$R_y(-\theta)$ゲートを加えた回路

をつくり、これとCXゲートを組み合わせて3量子ビットの回路を構成します。回転角のパラメータとしては$\theta_1,\theta_2$の2つとします。
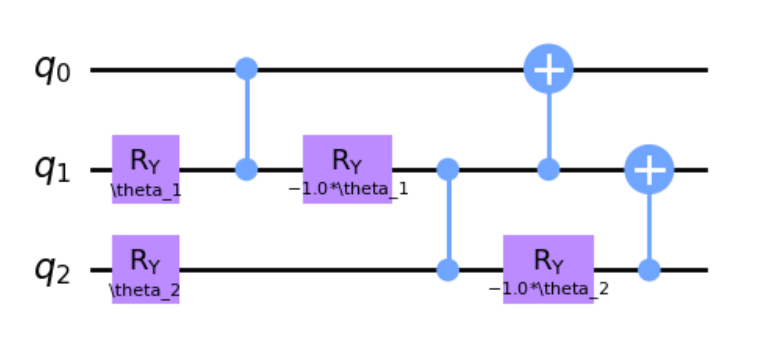
この回路は3量子ビットのパラメータ化されたW-stateをつくる回路で、インプットとして$\ket{q_0 q_1 q_2} = \ket{100}$を与えたときに、アウトプットの量子状態として
\cos \theta_1 \ket{100} - \sin \theta_1 \cos \theta_2 \ket{010} + \sin \theta_1 \sin \theta_2 \ket{001}
が得られることが知られています([4])。この結果は量子ビットの位取りがQiskitのそれとは逆になっていることに注意してください。
こちらも前の例と同様にQiskitで回路を定義し、qiskit_to_tk関数、circuit_to_symbolic_unitary関数を使って行列表現を求めるのですが
pytketにより記号演算で得られた行列に$\ket{100}$をかけた結果と一致するかどうか確認するため、ビット列の順序を反転せずに計算します。計算結果の一部のキャプチャを示しますが、全てを載せるのはかなりの分量になるため省略します。
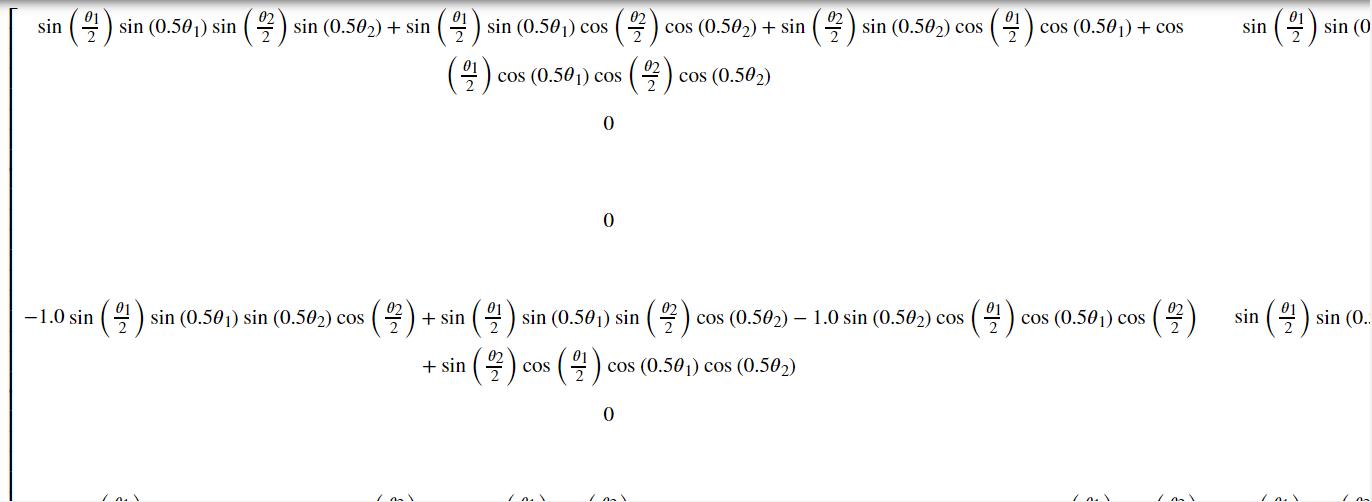
上記のキャプチャからもわかりますが、行列の各要素の計算式の簡約化がされていないため、既知の結果とpytketによる計算結果と一致するかどうかを確かめるにはもう一段工夫が必要です。
5.Sympyによる簡約化
Pythonでの数式処理であればSympyを考えますが、Sympyには数式を簡約化するためにSimplify関数([5])が提供されています。さらにExperimental LaTeX Parsingとして、LaTeXでの数式表現からSympyの数式表現に変換するparse_latex関数([6])があるので、これらを組み合わせて簡約化ができないか考えます。
pytketのcircuit_to_symbolic_unitary関数によって得られた行列は、Jupyter Notebook上ではグラフィカルに表示されています。この行列の表示上にマウスカーソルを移動して右クリックすると、Show Math as →の表示が現れるので、TeX Commandsを選択すると、Mathjax Equation Source という別ウィンドウが開きLaTeXでの表示を得ることができます。

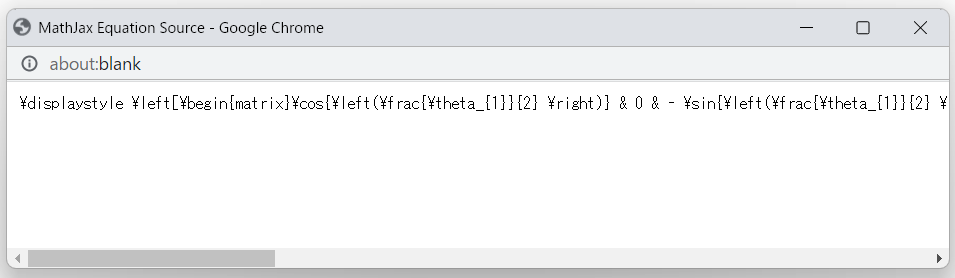
このウィンドウから、行列の各要素をコピーし、parse_latex関数、Simplify関数を使うことで簡約化することができます。
例えば、先ほど計算したW-stateを表わす3量子ビットの回路について、行列を表わすLaTeXの表現から切り出した1行1列目の要素は

となっています。
LaTeXで清書すると

となります。式中の分数の2分の1と0.5は、circuit_to_symbolic_unitaryによる出力をそのまま表示しています。
これをparse_latex関数、Simplify関数を使って簡約化してみると、結果は $1$ となりました。

この作業を行列の要素の数だけ繰り返せばよいのですが、LaTeXでの行列の各要素を文字列のデータとしてとっておき、このデータを読み込んでparse_latex関数、Simplify関数を適用するプログラムを作り、処理しました。その結果を清書すると以下のとおりです。

この行列に
\ket{100} = [0 \ \ 0 \ \ 0 \ \ 0 \ \ 1 \ \ 0 \ \ 0 \ \ 0]^{T}
をかけてみると、
[0 \ \ \sin \theta_1 \sin \theta_2 \ \ -\sin \theta_1 \cos \theta_2 \ \ 0 \ \ \cos \theta_1 \ \ 0 \ \ 0 \ \ 0]^{T}
となりますので、前述の結果([4])
\cos \theta_1 \ket{100} - \sin \theta_1 \cos \theta_2 \ket{010} + \sin \theta_1 \sin \theta_2 \ket{001}
と一致することがわかります。
6.まとめ
実際に3量子ビットの回路ではpytketやSympyを援用して、手計算による結果の確認に使えそうだという感触をもちました。
現状では、pytketのcircuit_to_symbolic_unitary関数には行列の要素を簡約化する処理は入っていないようなので、得られた式を上記で紹介したような方法で整理する必要があります。
pytketやSympyの関数のドキュメントを読むと、計算量が多くなるので実用的なのは数量子ビットくらいまでであるとか、experimentalという扱いである、としており実際の応用には限界があると感じました。現状では個々の回路の特性を踏まえ、それに合う計算のしかたを考えて工夫するのがよさそうです。
他にも同様の方法はあるかと思いますが、機会があればMathematicaにおける取り扱いを調べてみたいと考えます。この話題について詳しい方がおられましたら、コメント等いただければ幸いです。
7.使用した環境、バージョン
ここで示したプログラム等はWindowsマシンを使い、Python 3.10.4で実行しています。
Qiskitなどのライブラリのバージョンは以下のとおりです。
qiskit 0.40.0
qiskit-aer 0.11.2
pytket 1.11.1
pytket-qiskit 0.35.0
sympy 1.11.1
参考文献およびサイト
[1] https://quantumcomputing.stackexchange.com/questions/16927/symbolic-computation-with-quantum-circuits
[2] https://quantumcomputing.stackexchange.com/questions/29384/is-it-possible-to-get-the-symbolic-matrix-operator-associated-with-a-parameter
[3] https://cqcl.github.io/tket/pytket/api/
[4] Matsuo Atsushi,Suzuki Yudai and Yamashita Shigeru, Problem-specific Parameterized Quantum Circuits of the VQE Algorithm for Optimization Problems, https://arxiv.org/abs/2006.05643
[5] https://docs.sympy.org/latest/tutorials/intro-tutorial/simplification.html
[6] https://docs.sympy.org/latest/modules/parsing.html#experimental-mathrm-latex-parsing