ベクトル/行列演算の定番ライブラリEigen

#ベクトル/行列演算の定番ライブラリEigen (日本語解説のサイトまとめと便利な機能紹介)

##Eigenとは
C++の行列/ベクトルを扱うライブラリ(公式)．

Eigenの主な特長

• 行列演算を直感的に書くことが出来る．
• ヘッダーファイルのみのライブラリのため，ライブラリのビルドやリンクが必要なく組み込やすい．
• 高速．他のライブラリとの比較ベンチマークはこちら(公式)

##解説サイト(すべて日本語)

1. Eigen - C++で使える線形代数ライブラリ(でらうま倶楽部)- 基本的な使い方とも幾何変換，クォータニオンなどの解説もあり．
2. Eigen ー C++で線形代数を！(singular point)- 3回のポストで，幅広い機能について解説している．
3. Robotics/Eigen(NAIST::OnlineText)- 基本的な機能の他に行列分解についても解説あり．

Eigenの使い方

Eigenはヘッダーのみのライブラリなので，ビルドやリンクは必要ない．
インクルードディレクトリにEigenのディレクトリに追加し，#includeするのみでOK．

#include <Eigen/Core> // 行列演算など基本的な機能．

Eigenの設定

Eigenはヘッダーオンリーのライブラリなので，ライブラリに関する設定はプリプロセッサで行う．Eigenのヘッダーをインクルードする前にマクロを定義することに注意．

// 1. マクロを定義．
#define EIGEN_NO_DEBUG // コード内のassertを無効化．
#define EIGEN_DONT_VECTORIZE // SIMDを無効化．
#define EIGEN_DONT_PARALLELIZE // 並列を無効化．
#define EIGEN_MPL2_ONLY // LGPLライセンスのコードを使わない．

// 2. Eigenをインクルード．
#include <Eigen/Core>

マクロの一覧はこちらhttps://eigen.tuxfamily.org/dox/TopicPreprocessorDirectives.html

配列のメモリ配置(Eigen::ColMajor/Eigen::RowMajor)

• 二次元配列には，メモリ空間上の並び順ColMajorとRowMajorがある．
• Eigenだけを使っているだけでは気にしなくてもよいことが多いが，Eigen::Mapなどメモリ扱う場合には，ColMajor/RowMajorを意識する必要がある．
• EigenはデフォルトでCol-major(列優先)なので，特にRowMajorで確保された配列を扱うときに注意．

/**
* もしmがColMajorならば，1 4 2 5 3 6
* もしmがRowMajorならば，1 2 3 4 5 6
*/
Matrix<int, 2, 3> m; // [2x3]の行列
m << 
  1, 2, 3,
  4, 5, 6;

for(int i=0; i<m.size(); ++i){
  std::cout << *(m.data()+i) << "　";
}

RowMajor(行優先)を使う

/** 
* 1. マクロで定義するパターン．
* デフォルトがRowMajorになる．
*/
#define EIGEN_DEFAULT_TO_ROW_MAJOR

/**
* 2. 型で指定するパターン．
* RowMajorとColMajorを混在させることもできる．
*/
Eigen::Matrix<float, -1, -1, Eigen::RowMajor>;

##パフォーマンスを最適化する設定 (Visual studioの場合)
並列化やSIMD演算を有効にすることで高速化する．デバッグの無効化については自己責任で．( 公式ドキュメント1,公式ドキュメント2)

OpenMPの有効にする．

(プロジェクトのプロパティ⇒C/C++⇒言語⇒OpenMPをYesに設定)

SIMDのサポートを有効にする．

(プロジェクトのProperty⇒C/C++⇒Code Generation⇒Enable Enhanced Instructionから有効にする命令を選択する)

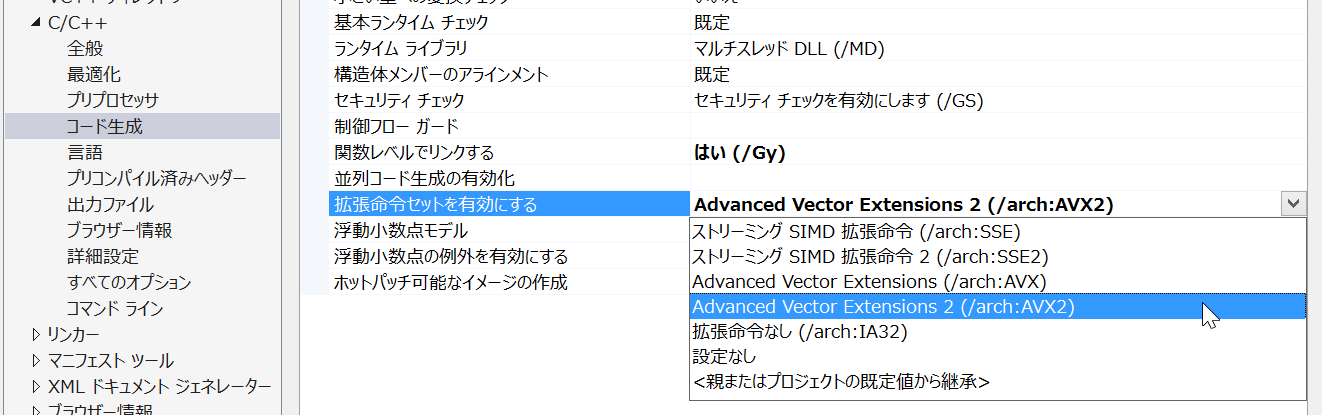
有効になっているSIMD命令を確認する方法

Eigen::SimdInstructionSetsInUse()を用いる．

std::cout << Eigen::SimdInstructionSetsInUse() << std::endl;
//出力例: AVX SSE, SSE2, SSE3, SSSE3, SSE4.1, SSE4.2

SIMDの効果を確認するサンプルコード

//
// 行列積でSIMDの効果を確認するコード．
//
#include <iostream>
#include <chrono>
//#define EIGEN_DONT_VECTORIZE
#include <Eigen/Core>

int main(){
    // 有効になっているSIMD命令を表示．
    std::cout << "Available :SIMD Instructions: "<< Eigen::SimdInstructionSetsInUse() << std::endl;
    
    const int d = 128; // 行列の次元．
    const int n = 10000; // 繰り返し回数．

    Eigen::VectorXd t(n); // 時間格納用．
    for (int i = 0; i < n; ++i) {
        Eigen::MatrixXf m1 = Eigen::MatrixXf::Random(d, d);
        Eigen::MatrixXf m2 = Eigen::MatrixXf::Random(d, d);
        
        const auto start = std::chrono::system_clock::now();
        m1*=m2;
        const auto end = std::chrono::system_clock::now();

        t[i] = std::chrono::duration_cast<std::chrono::microseconds>(end - start).count(); //処理に要した時間をミリ秒に変換
    }
    std::cout << "Average: " << t.mean() << " ms." <<std::endl;
    return 0;
}

著者の環境での実行結果

• SIMDなし(#define EIGEN_DONT_VECTORIZEして実行): 861.54ms

• SIMDあり(#define EIGEN_DONT_VECTORIZEをコメントアウトして実行): 149.527ms

##便利な機能
###確保済みの配列からEigen型に変換 Eigen::Map

• Eigen::Map を用いることで，確保済みの領域でEigenのオブジェクトを生成可能．コピーが発生しないので既存のコードの一部アルゴリズムをEigenで置き換えるときなどに便利．
• 例えば，Eigen::Map<Eigen::Vector3d>はEigen::Vector3dと同様に使うことができる(公式ドキュメント)．

/**
* std::vectorからEigen::Vector3dを生成．
*/
std::vector<double> vec_std(3);
vec_std[0] = 1.0;
vec_std[1] = 2.0;
vec_std[2] = 3.0;

Eigen::Map<Eigen::Vector3d> vec(vec_std.data()); // Eigen::Vector3dとして使える．

###行列，ベクトルの最大/最小値とそのインデックスを取得
maxCoeff(), minCoeff()を使って値とインデックスを取得できる．(公式ドキュメント)

//ベクトル型
Eigen::VectorXf::Index maxId;
float max = v.maxCoeff(&maxId);
Eigen::Vector3dXf::Index minId;
float min = v.maxCoeff(&minId);

//行列型
Eigen::MatrixXf::Index maxRow, maxCol;
float max = m.maxCoeff(&maxRow, &maxCol);
Eigen::MatrixXf::Index minRow, minCol;
float min = m.minCoeff(&minRow, &minCol);