クーン・ポーカーの最適な混合戦略ナッシュ均衡

■ はじめに

単純化された2人ポーカー「クーン・ポーカー」の最適な混合戦略ナッシュ均衡については、論文 [1] やウィキペディア [2] で示されているが、その導出方法の説明が不足しているため、本稿では導出方法を具体的に詳述する。

■ ナッシュ均衡

ナッシュ均衡について簡単に説明しておく。
ナッシュ均衡とは、「他のプレーヤーの戦略を所与とした場合、 どのプレーヤーも自分の戦略を変更することによってより高い利得を得ることができない戦略の組み合わせ」 と定義される（wikipedia より引用）。
例えば、通常のジャンケンにおいては、グー・チョキ・パー をそれぞれ 1/3 の確率でランダムに選択するのがナッシュ均衡戦略となる。 これは、相手がどの手をどのような確率で選択しても期待利得が±0であり、 戦略を変更してもより高い利得を得ることができないからである。
もし相手がグーを100%出すのであれば、パーを100%出せば、期待利得は +1 となり、 ナッシュ均衡戦略よりも期待利得が高くなる。だが、この場合相手がチョキを100%出すように戦略を変更すると、相手の期待利得が +1 になってしまう。 相手が戦略を変更することでより高い利得を得ることが可能なので、これはナッシュ均衡戦略ではない。
つまり、ナッシュ均衡戦略は最高の利得期待値を得るものではなく、相手に戦略の選択肢を与えず、損をしない戦略とも言える。

■ クーン・ポーカー

「クーン・ポーカー」はクーン氏の論文 [1] で紹介されている最も簡単なポーカーバリエーションのひとつだ。
ランク（数字）の異なる3枚のカード（例えば J、Q、K）を使用する。スート（マーク）は関係なく、ランクの大きいカードが勝つ（K > Q > J）。
2人でプレイする（ヘッズアップ）ゲームで、1勝負のアンティ（参加費）は1チップだ。
3枚のカードからなるデッキをシャフルし、プレイヤーに1枚ずつ配る。プレイヤーは交互に以下の4つのアクション（行動）が可能:

• Check: 何も行動せず、手番を相手に渡す。
• Raise: 掛け金を1チップ上げる。Raiseされた場合、Checkはできない。
• Fold: 手札を捨て、その勝負を降りる。
• Call: Raiseに対して同額を賭ける。

Raiseは1勝負につき1回のみ可能で、Re-Raiseは不可だ。相手がFoldすれば、手札の強弱に関係なく勝利する。
Check→Check または Raise→Callの場合は、ショーダウン（手札を晒すこと）となり、ランクの大きいカードを持つプレイヤーが勝利する（+1 または +2）。

ゲーム木

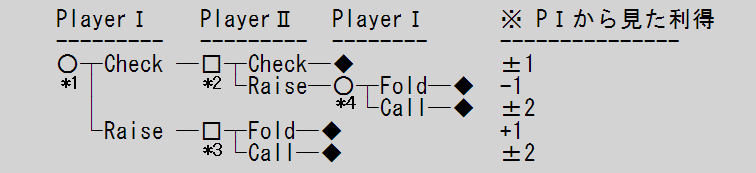
先手（Player-I）は、自分の手札を見て、Check または Raise を選択できる。後手（Player-Ⅱ）は、先手がCheckした場合はCheckまたはRaise、先手がRaiseした場合はFoldまたはCallを選択できる。後手がRaiseした場合は、先手がFoldまたはCallを選択できる。

下図にクーンポーカーのゲーム木全体を示す。

図１:

状態は ○、□、◆ノードで表記し、それぞれプレイヤーⅠの手番、Ⅱの手番、末端（勝敗がついた状態）を表す。
親子ノードは線分（ブランチ・枝）で結合され、その間にアクションを記述する。
複数のアクションが可能な場合、枝が分岐し複数の子ノードを記述する。
なお、Raise されていない状態での Fold は意味が無いので行わないものとする。
プレイヤーのアクション選択が必要なノードはわずか４（上図 *1～*4）で、手札は３種類なので、それぞれの最適戦略を考える必要があるのは、わずか12の場合しかない。したがって、下表の12個所について最適戦略を求めればよいことになる。

表１：

手札\状態	*1 初期状態	*2 先手Check直後	*3 先手Raise直後	*4 後手Raise直後
J
Q
K

次章でそれぞれの場合についての最適戦略を示す。

■ 最適戦略

非ナッシュ均衡最適戦略

まずは、ナッシュ均衡とは無関係に最適な戦略がヒューリスティックに決まる状況・手札について述べる。
自分の手札がKの場合に、相手がRaiseしてきた場合、相手の手札はJまたはQなので、ショーダウンになれば必ず勝てる。したがって、100% Callするのが最適な戦略である。
一方、自分の手札がJの場合に、相手がRaiseしてきた場合、相手の手札はQまたはKなので、Callしショーダウンになれば必ず負けてしまい、-2の利得となる。そのため、0% Call するのが最適である。これにより、チップ損失を-1に抑えることができる。
また、後手の手札がKの場合に、先手がCheckした場合は、100%Raiseするのが最適である。なぜなら、後手もCheckすれば+1の利得しか得られないが、Raiseすれば先手がCallするかもしれず、そうなれば利得が+2になるからである。

以上をまとめると各状態・手札での最適な混合戦略は下表のようになる。

表２：

手札\状態	初期状態	先手Check直後	先手Raise直後	後手Raise直後
J			0%Call	0%Call
Q
K		100%Raise	100%Call	100%Call

次に、手札がQで、Raise可能な場合のアクションについて考える。
まずは、計算が簡単な後手の場合。
後手がRaise可能ということは、先手がCheckしたということなので、後手がCheckするとショーダウンとなる。この場合先手の手札はJまたはKで、それぞれが50%の確率だとすると、後手の期待利得は±０となる（※ 実は最適な混合戦略ナッシュ均衡ではCheckされた場合のカードはJの確率がKの確率よりも高く、後手の期待利得は±０より大きくなる）。
QがRaiseした場合、先手の手札がJであれば100% Fold、Kであれば100% Callなので、後手の期待利得は (1 - 2) /2 = -0.5 となる。これは後手がCheckした場合の期待値より小さく、手札Qの後手はRaiseすると損なので100%Checkすることになる。

先手の手札がQで初手にRaiseした場合、後手の手札がJまたはKで、それぞれ100% Fold、100% Callなので、先手の期待利得は -0.5 となる。
先手が初手にCheckした場合は、後手の手札の種類によって状況が複雑になる。後手の手札がKの場合、100%Raiseし、QのCall確率は1/3なので、先手の期待利得は -2/3 + -2/3 = -4/3 となる。一方、後手の手札がJの場合、1/3の確率でRaise、2/3の確率でCheckとなるので、先手の期待利得は 1/3*(2/3 + -2/3) + 2/3*1 = 2/3 となる。
ここで、後手がJの手札でRaiseする確率が1/3であり、QがRaiseされてCallする確率も1/3であるのは、クーン・ポーカーにおける最適な混合戦略ナッシュ均衡に基づいている。その詳細は後述する。
以上より、先手の手札がQで初手にCheckした場合の期待利得は (-4/3 + 2/3)/2 = -1/3 となる。これは、初手にRaiseした場合の期待利得である -0.5 よりも大きい（損失が少ない）ので、常にCheckするのが最善の戦略となる。

以上をまとめると各状態・手札での最適な混合戦略は下表のようになる（※ 表では常に強気の行動をとる確率を表記することにしているので、100% Call ではなく 0% Raise と表記している）。

表３：

手札\状態	初期状態	先手Check直後	先手Raise直後	後手Raise直後
J			0%Call	0%Call
Q	0%Raise	0%Raise
K		100%Raise	100%Call	100%Call

ナッシュ均衡最適戦略

以上で、ナッシュ均衡とは関係なく、ヒューリスティックに最適戦略が決まる状態・手札について最適戦略を求めた。ここからナッシュ均衡となる最適な混合戦略を求めていく。

まずは先手の手札がJの場合を考える。
先手がCheckした場合、後手の手札はQまたはKなので、Checkされると利得は-1、Raiseされても手札がJなら100% Foldするため、利得は-1となる。したがって、先手がCheckした時の利得は-1である。

一方、先手がRaiseした場合、後手の手札がKなら100% Callされ、利得は-2となる。後手の手札がQだった場合、QのRaise確率をPとすると、先手の利得は -2P + (1-P) となる。後手の選択が最適な混合戦略ナッシュ均衡となるためには、先手がRaiseした時の期待利得をCheckした時と同じ-1にすればよい。すなわち、(-2 + -2P + (1-P))/2 = -1、これを解くと P = 1/3 となる。

次に、先手の手札がKの場合を考える。
先手がRaiseし、後手の手札がQだった場合、後手は先手がJでRaiseしたのかKでRaiseしたのかはわからないので、Jの場合同様に1/3の確率でCallする。後手の手札がJだった場合は100%Foldだ。したがって、先手がRaiseした場合の期待利得は ((2/3 + 2/3) + 1)/2 = 7/6 となる。
一方、先手がCheckした場合、後手の手札がQだった場合はCheck、Jだった場合は1/3の確率でRaiseする（その理由は後術）ので、先手の期待利得は (1 + (2/3 + 2/3))/2 = 7/6 となる。

以上より、先手の手札がJまたはKの場合、それぞれのRaise確率をαとβとする任意の確率でRaiseしても、後手がQのとき1/3の確率でCallすれば、先手の期待利得は一定となる。したがって、Raiseされた場合、後手Qの最適な混合戦略ナッシュ均衡は1/3の確率でCallすることとなる。

以上をまとめると各状態・手札での最適な混合戦略は下表のようになる。

表４：

手札\状態	初期状態	先手Check直後	先手Raise直後	後手Raise直後
J	α Raise		0%Call	0%Call
Q	0%Raise	0%Raise	100/3%Call
K	β Raise	100%Raise	100%Call	100%Call

※ α, β は 0 ≦ P ≦ 1 の範囲

次は、初手の手札がJまたはK,後手の手札がQの場合に、初手のRaise確率を調整し、後手QがCallしてもFoldしても期待利得が同一で、ナッシュ均衡なるようにする。
先手がRaiseしたとき、先手の手札がJである確率をP、Kである確率を(1-P)としたとき、後手QがCallした場合の先手期待利得は -2P + 2*(1-P) となる。ナッシュ均衡にするには、後手がFoldした場合の期待利得である +1 と同じにすればよいので、-2P + 2*(1-P) = 1。これを解くと P = 1/4 となる。すなわち、先の β を 3*α とすればよいことになる（ただし、0 ≦ β ≦ 1 なので 0 ≦ α ≦ 1/3）。
また、この考え方は、先手Check後の後手の場合でも同様で、KのRaise確率が 1 なので、J のRaise確率を 1/3 にするとよいことになる。

以上をまとめると各状態・手札での最適な混合戦略は下表のようになる。

表５：

手札\状態	初期状態	先手Check直後	先手Raise直後	後手Raise直後
J	α Raise	100/3%Raise	0%Call	0%Call
Q	0%Raise	0%Raise	100/3%Call
K	3α Raise	100%Raise	100%Call	100%Call

※ αは 0 ≦ P ≦ 1/3 の範囲

テーブルもほとんど埋まった。残りは先手手札がQで先手Check→後手Raise直後の場合のみだ。
この場合も先手Raise直後の場合と同様に、後手の手札がJの場合に、CheckでもRaiseでも期待利得が同じ値になるようにする。後手がCheckした場合は、その時点でショーダウンとなり、先手利得は +1 となる。
Raise した場合は、先手がKであれば100%Callなので先手利得 +2、Qであれば確率1/3でCallすれば、先手利得は 2*1/3 - 2/3 = 0 となり、先手期待利得は +1 となる。

したがって、各状態・手札での最適な混合戦略は下表のようになる。

表６：

手札\状態	初期状態	先手Check直後	先手Raise直後	後手Raise直後
J	α Raise	100/3%Raise	0%Call	0%Call
Q	0%Raise	0%Raise	100/3%Call	100/3%Call
K	3α Raise	100%Raise	100%Call	100%Call

※ αは [0, 1/3] の範囲

■ 期待利得

次章で、「1/3 + α」が誤りであることを直接的に証明するのだが、その前に、各手札での期待利得を計算しておく。
双方が最適な混合戦略ナッシュ均衡を採った場合のプレイヤー1（先手）の期待利得は以下のようになる。

表７：

手札	Player-1	Player-2	Player-1	実現確率*先手期待利得
J, Q	(1-α) Check	Check		(1-α) * (-1) = α-1
	α Raise	2/3 Fold		α * 2/3 * 1 = 2/3 * α
		1/3 Call		α * 1/3 * (-2) = -2/3 * α
J, K	(1-α) Check	Raise	Fold	(1-α) * (-1) = α-1
	α Raise	Call		α * (-2) = -2 * α

プレイヤー1 の手札がJの場合の期待利得：
(α-1 + -2/3 * α + 2/3 * α + α-1 - 2α) / 2 = -1

表８：

手札	Player-1	Player-2	Player-1	実現確率*先手期待利得
Q, J	Check	2/3 Check		2/3 * 1 = 2/3
		1/3 Raise	2/3 Fold	1/3 * 2/3 * (-1) = -2/9
			1/3 Call	1/3 * 1/3 * 2 = 2/9
Q, K	Check	Raise	2/3 Fold	2/3 * (-1) = -2/3
			1/3 Call	1/3 * (-2) = -2/3

プレイヤー1 の手札がQの場合の期待利得：

(2/3 - 2/9 + 2/9 - 2/3 - 2/3) / 2 = -1/3

表９：

手札	Player-1	Player-2	Player-1	実現確率*先手期待利得
K, J	(1-3α) Check	2/3 Check		(1-3α) * 2/3 * 1 = 2/3 - 2α
		1/3 Raise	Call	(1-3α) * 1/3 * 2 = 2/3 - 2α
	3α Raise	Fold		3α * 1 = 3α
K, Q	(1-3α) Check	Check		(1-3α) * 1 = 1 - 3α
	3α Raise	2/3 Fold		3α * 2/3 * 1 = 2α
		1/3 Call		3α * 1/3 * 2 = 2α

プレイヤー1 の手札がKの場合の期待利得：

(2/3 - 2α + 2/3 - 2α + 3α + 1 - 3α + 2α + 2α) /2 = 7/6

先手,後手手札に対する期待利得が複数あるとわかりずらいので、下記に各手札状態ごとの先手期待利得を示しておく。

表10：

先手,後手手札	先手期待利得
J, Q	-1 + α
J, K	-1 - α
Q, J	2/3
Q, K	-4/3
K, J	4/3 - α
K, Q	1 + α

したがって、先手の期待利得は (-1 + α - 1- α + 2/3 - 4/3 + 4/3 - α + 1 + α) / 6 = -1/18 となる。

クーン・ポーカーは先手・後手に対して対照的なルールであるが、後手は先手の初手行動を見て行動を決めることができる分、若干後手が有利ということになる。

■ 最後に

単純化された2人ポーカーである「クーン・ポーカー」の最適な混合戦略ナッシュ均衡の導出について解説した。
本稿の執筆にあたり、筆者の話を辛抱強く長時間聞いてくれた方々に感謝の意を表したい。

参考文献

[1] Kuhn, H. W. (1950). "Simplified Two-Person Poker". In Kuhn, H. W.; Tucker, A. W. (eds.). Contributions to the Theory of Games. Vol. 1. Princeton University Press. pp. 97–103.

[2] "Kuhn Poker", wikipedia（ https://en.wikipedia.org/wiki/Kuhn_poker ）
"クーン・ポーカー", wikipedia（ https://ja.wikipedia.org/wiki/クーン・ポーカー ）