はじめに
今回はA~Cがコンテスト中に解けて、コンテスト後にDも解けたのでDまで解説しようと思います。
では、解説していきます。
A - Growth Record
問題文はこちら
文章、制約を読み込んでみましょう。
「高橋君はN歳になった」と書いてあり、その時の身長はT[cm]だと記述してあります。
また、それ以下の文章を要約すると「0~X歳まで身長がD[cm]ずつ伸び続け、それ以降はずっと変化していない」ということを言っています。
ここで制約に着目すると、M<N、X≦Nとあることから
「大人になった高橋君の身長はTです。X歳まで成長期で毎年D[cm]ずつ伸びていたとするとM歳の時何cmでしたか?」
と読み替えることもできます(サンプル見た感じN=1もあるので高橋君が大人とは限らないですが…)。
ということで、X≦MならTをそのまま、X>MならX歳よりもX-M歳だけ下なのでTから(X-M)×M[cm]引いたものを出力すれば良いです。
class Main{
public static void main(String[] args)throws IOException{
//ライブラリのオブジェクト生成
Library Sys = new Library();
//一行を空白区切りで取得後、数値に変換
String[] str = Sys.reads(" ");
int N = Sys.parseInt(str[0]);
int M = Sys.parseInt(str[1]);
int X = Sys.parseInt(str[2]);
int T = Sys.parseInt(str[3]);
int D = Sys.parseInt(str[4]);
//MがXより大きい時はT
if(X<M) System.out.println(T);
//MがX以下ならXの何歳下か計算してその分だけTから減らす
else Sys.out.println(T+(M-X)*D);
//フラッシュ代わりのclose
Sys.out.close();
}
}
コンテスト中、Nを使わないことを不安に思って提出を躊躇してしまいました…。自信が欲しい。
B - Counterclockwise Rotation
問題文はこちら
複素数や行列の知識を使えばサクッと解けるらしいですが、そんな知識は持ち合わせていないので原始的に計算してやりました。
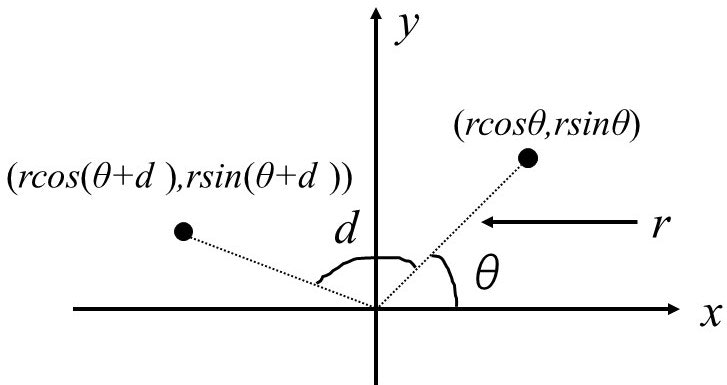
移動前の点と原点を結ぶ直線とx軸が成す角をθとすると、移動後の点と原点を結ぶ直線とx軸が成す角はθ+dとなります。また、原点と点との距離rは三平方の定理から求めることができます。よって、三角関数を用いて移動後の座標を計算することができます(下図参照)
後はこの式を実装するのみです。
なお、Math.acos(double)は戻り値が0≦θ≦πなので、最初の点のy座標が負の時は-Math.acos(double)を用いる必要があります。ご注意ください。
class Main{
public static void main(String[] args)throws IOException{
//ライブラリのオブジェクト生成
Library Sys = new Library();
//Stringで一旦受け取って数値変換
String[] str = Sys.reads(" ");
int a = Sys.parseInt(str[0]);
int b = Sys.parseInt(str[1]);
int d = Sys.parseInt(str[2]);
//原点なら(0,0)のまま(後々のNaNを避けるため)
if(a==0&&b==0){
System.out.println(0+" "+0);
System.exit(0);
}
//原点からの距離
double len = Math.sqrt(a*a+b*b);
//x軸と成す角の角度(反時計回り)
double rad = b<=0?-Math.acos(a/len):Math.acos(a/len);
//移動後のx、yの値を求める
double x = len*Math.cos(rad+Math.toRadians(d));
double y = len*Math.sin(rad+Math.toRadians(d));
//念のため小数第8位まで出力しておく
System.out.printf("%8f",x);
System.out.print(" ");
System.out.printf("%8f",y);
//flush代わりのclose
Sys.out.close();
}
}
acosの戻り値を全然気にしてなかったのでペナルティをいっぱい頂いてしまいました…。悲しい…。
C - XX to XXX
問題文はこちら
文字列を参照して挿入して…とかやってるとよくわからなくなりそうなので、挿入できる場合は参照する場所を変化させないことで擬似的に挿入させる手法をとってみます。
for文だとループの度にi++、j++が行えますが、ループ内でi--を行なうことでiを一定に保てます。これを利用して先頭から一致しているか見ていけば楽に解けますね。
class Main{
public static void main(String[] args)throws IOException{
//ライブラリのオブジェクト生成
Library Sys = new Library();
//S、Tをchar型配列として受け取り
char[] S = Sys.read().toCharArray();
char[] T = Sys.read().toCharArray();
//連続しているか(文字を挿入できるか)を管理する変数
boolean canInsert = false;
//最初から違うなら終わりで(やんなくても良いかも?)
if(S[0]!=T[0]){
Sys.out.println("No");
Sys.out.close();
System.exit(0);
}
//何番目の文字を見ているか記録する変数
int i=1,j=1;
//先頭から見ていく
for(;j<T.length;i++,j++){
//端まで来てしまったか?
if(i==S.length){
//直前まで連続してたなら一番後ろを参照するようにする
if(canInsert)
i--;
//Sに挿入できないなら終わり
else{
Sys.out.println("No");
Sys.out.close();
System.exit(0);
}
}
//文字が違う?
if(S[i]!=T[j]){
//挿入できる条件を満たしていて、挿入したらTと同じか?
if(S[i-1]==T[j]&&canInsert)
i--;
//挿入できないなら終わり
else{
Sys.out.println("No");
Sys.out.close();
System.exit(0);
}
}
//連続しているならtrue、してないならfalseに変えとく
if(i!=0&&S[i-1]==S[i])
canInsert = true;
else
canInsert = false;
}
//どっちもちょうど終わりのタイミング?
if(i==S.length&&j==T.length)
Sys.out.println("Yes");
else
Sys.out.println("No");
//flush代わり
Sys.out.close();
}
}
個人的にこの問題が一番楽だったような…そんな感じでした(単純に数学が苦手?)
D - Circumferences
問題文はこちら
何やらUnion Findってものやグラフってものを使って解けるらしいですが、私にそんなアルゴリズム力は無いので普通に隣り合っているものを順に見ていくBFSで実装してやりました。
円が接する、もしくは交差する条件は「中心同士の距離が二つの円の半径の合計以下」と「半径の差が中心同士の距離以下」を同時に満たせば良いので(前者は円同士が"外部"で接しているか交差している条件、後者は円同士が"内部"で接しているか交差している条件です)、これを条件文にして判定します。
なお、接しているか調べる際に距離を算出する必要がありますがMath.sqrtを使ってしまうと誤差が出やすいので二乗のまま計算してあげましょう(二乗するのでint型はオーバーフローが心配です。long型を使いましょう)。
BFS自体は典型的な実装ですが、一度Listに入れた円を重複して入れないようにboolean型配列などで探索済みか記録するようにしましょう。
class Main{
public static void main(String[] args)throws IOException{
//ライブラリのオブジェクト生成
Library Sys = new Library();
//Nとスタート、ゴール、円の情報の取得
int N = Sys.readInt();
String[] str = Sys.reads(" ");
long sx = Sys.parseLong(str[0]);
long sy = Sys.parseLong(str[1]);
long tx = Sys.parseLong(str[2]);
long ty = Sys.parseLong(str[3]);
long[][] circle = new long[N][3];
for(int i=0;i<N;i++){
str = Sys.reads(" ");
circle[i][0] = Sys.parseLong(str[0]);
circle[i][1] = Sys.parseLong(str[1]);
circle[i][2] = Sys.parseLong(str[2]);
}
//探索済みの円か管理する配列
boolean[] isUsed = new boolean[N];
//スタートの円を探す
int now = -1;
for(int i=0;i<N;i++){
long x = Math.abs(sx-circle[i][0]);
long y = Math.abs(sy-circle[i][1]);
if(x*x+y*y==circle[i][2]*circle[i][2]){
now = i;
break;
}
}
//ゴールの円を探す
int fin = -1;
for(int i=0;i<N;i++){
long x = Math.abs(tx-circle[i][0]);
long y = Math.abs(ty-circle[i][1]);
if(x*x+y*y==circle[i][2]*circle[i][2]){
fin = i;
break;
}
}
//BFSで解く
ArrayList<Integer> list = new ArrayList<Integer>();
list.add(now);
while(list.size()>0){
int temp = list.get(0);
list.remove(0);
//ゴールなら終了
if(temp==fin){
System.out.println("Yes");
System.exit(0);
}
//今の場所は探索済みにする
isUsed[temp] = true;
for(int i=0;i<N;i++){
//探索済みならスルー
if(isUsed[i])continue;
//円が接しているor交差しているか調べる
long x = Math.abs(circle[temp][0]-circle[i][0]);
long y = Math.abs(circle[temp][1]-circle[i][1]);
long r = circle[temp][2]+circle[i][2];
long rsub = Math.abs(circle[temp][2]-circle[i][2]);
if(x*x+y*y<=r*r&&x*x+y*y>=rsub*rsub){
//交差しているならArrayListに積む
isUsed[i] = true;
list.add(i);
}
}
}
//whileを抜けた=ゴールにたどり着けなかったのでNo
System.out.println("No");
}
}
うーん…これくらいなら解きたかったですね…悔しい…。
感想
A:問題文が少々理解できなくて時間がかかった。
B:数学らしい問題でちょっと楽しかった(速く解けたわけではない)。
C:可能な限り早く実装できるようにしておきたい問題。比較的易しい?
D:最初実装法が思いつかなくてちょっと身構えてしまった。実装自体は割と簡単なので慣れておきたい。
って感じでした。
数学色が強い気もしましたが、まぁプログラミングなんて数学ですからね。A~Dくらいは解けるようにしておきたいと思いました(個人の意見)。