はじめに
今回はコンテスト中にEまで、コンテスト後にGまで解けたのでそれを載せようと思います。
では見ていきましょう。
なお、ライブラリの内容は提出結果より確認出来ます。
A - Double Click
問題文はこちら
先頭から見ていって、差が$D$以下の箇所を見つけたら時間を変数に入れてループを抜けることで一番最初の時刻を出力させました。
final class Main {
private static final boolean autoFlush = false;
private static final SimpleScanner sc = new SimpleScanner( System.in );
private static final SimplePrinter out = new SimplePrinter( System.out, autoFlush );
public static void main ( String[] args ) {
//N、D、T1の受け取り
int N = sc.nextInt();
int D = sc.nextInt();
int T = sc.nextInt();
//答えを格納する変数(初期値は-1)
int ans = -1;
//T2~TNを順に見ていく
while(--N>0){
//次のクリックの時間の受け取り
int t = sc.nextInt();
//ダブルクリック判定?
if(t-T<=D){
//ansを更新してループを抜ける
ans = t;
break;
}
//クリックの時間を更新
T = t;
}
//答えの出力
out.println(ans);
out.close();
}
}
最初に$T_1$を受け取っているのでループ回数が$N-1$回になるようwhileの条件は--N>0になっています。
B - chess960
問題文はこちら
S.indexOf("B")とS.lastIndexOf("B")の偶奇が異なるか、S.indexOf("K")がS.indexOf("R")とS.lastIndexOf("R")の間かを判定することで解きました。
final class Main {
private static final boolean autoFlush = false;
private static final SimpleScanner sc = new SimpleScanner( System.in );
private static final SimplePrinter out = new SimplePrinter( System.out, autoFlush );
public static void main ( String[] args ) {
//Sの受け取り
String S = sc.next();
//各条件を満たしているか求める
boolean isTrue = true;
isTrue &= (S.lastIndexOf("B")-S.indexOf("B"))%2==1;
isTrue &= S.indexOf("R")<S.indexOf("K");
isTrue &= S.indexOf("K")<S.lastIndexOf("R");
//全部満たしていた?
out.println(isTrue?"Yes":"No");
out.close();
}
}
ユーザー解説にもありますが、正規表現を用いて解くこともできます。
C - PC on the Table
問題文はこちら
各$S$の中のTTを先頭から貪欲にPCに置き換えれば良いので、replaceメソッドを用いて解きました。
final class Main {
private static final boolean autoFlush = false;
private static final SimpleScanner sc = new SimpleScanner( System.in );
private static final SimplePrinter out = new SimplePrinter( System.out, autoFlush );
public static void main ( String[] args ) {
//H、W、Sの受け取り
int H = sc.nextInt();
int W = sc.nextInt();
String[] S = sc.next(H);
//各Sに対してreplaceメソッドを適用
for(int i=0;i<H;i++)
S[i] = S[i].replace("TT","PC");
//各Sを改行区切りで出力
out.println(S,"\n");
out.close();
}
}
比較的易しめですかね。
D - Count Subtractions
問題文はこちら
公式解説にありますが、引き算を行える回数を求めることで高速に処理することができると考えて、$A=B$になるまでそれを繰り返すことで答えを求めました。
final class Main {
private static final boolean autoFlush = false;
private static final SimpleScanner sc = new SimpleScanner( System.in );
private static final SimplePrinter out = new SimplePrinter( System.out, autoFlush );
public static void main ( String[] args ) {
//A、Bの受け取り
long A = sc.nextLong();
long B = sc.nextLong();
//回数を記録する変数
long ans = 0;
//条件を満たすまで繰り返す
while(A!=B){
//大きい方から小さい方を引けるだけ引く(大きい方が小さい方の倍数だったときの為に-1してから割り算している)
if(A<B){
ans += (B-1)/A;
B -= (B-1)/A*A;
}
else{
ans += (A-1)/B;
A -= (A-1)/B*B;
}
}
//回数の出力
out.println(ans);
out.close();
}
}
$A$、$B$が$0$になる時を考えるのがめんどくさいなと思って上記のように回数を求めました。
E - Kth Takoyaki Set
問題文はこちら
TreeSetを二つ準備し、片方のSet(以下Set1)に$A$を入れます。Set1の最小値を$v$とすると、Set1に各$i$に対する$v+A[i]$を、もう片方のSet(以下Set2)に$v$を入れることで、1から$K$番目までの金額をset2に構築することで、$K$番目の金額を求めました。Setを使っているので重複するものを考慮しなくてすみます。
final class Main {
private static final boolean autoFlush = false;
private static final SimpleScanner sc = new SimpleScanner( System.in );
private static final SimplePrinter out = new SimplePrinter( System.out, autoFlush );
public static void main ( String[] args ) {
//N、K、Aの受け取り
int N = sc.nextInt();
int K = sc.nextInt();
int[] A = sc.nextInt(N);
//小さい方から金額が確定しているもののset
TreeSet<Long> set = new TreeSet<>();
//保留中の金額のset
TreeSet<Long> thinking = new TreeSet<>();
//Aをthinkingに入れる
for(int i=0;i<N;i++)
thinking.add((long)A[i]);
//setにK個入るまで繰り返す
while(set.size()<K){
//現状一番小さい金額を取り出す
long now = thinking.pollFirst();
//now+A[i]をthinkingに入れる
for(int i=0;i<N;i++)
thinking.add(now+A[i]);
//now未満の金額はsetの中以外に存在しないのでsetに入れる
set.add(now);
}
//K番目=setで一番大きい数字を出力
out.println(set.pollLast());
out.close();
}
}
上記の実装だと構築途中でset1とset2に保持され得る要素数の合計は$N(K+1)$個以下なので、メモリに関しても心配する必要は無さそうです。
追記
set1の方はTreeSetを使わなくても、一番大きいものさえ保持出来れば良いのでlong型変数で処理できますね。
final class Main {
private static final boolean autoFlush = false;
private static final SimpleScanner sc = new SimpleScanner( System.in );
private static final SimplePrinter out = new SimplePrinter( System.out, autoFlush );
public static void main ( String[] args ) {
int N = sc.nextInt();
int K = sc.nextInt();
int[] A = sc.nextInt(N);
long ans = 0;
TreeSet<Long> thinking = new TreeSet<>();
for(int i=0;i<N;i++)
thinking.add((long)A[i]);
while(K-->0){
ans = thinking.pollFirst();
for(int i=0;i<N;i++)
thinking.add(ans+A[i]);
}
out.println(ans);
out.close();
}
}
F - Minimum Bounding Box 2
問題文はこちら
公式解説の通りです。内容は重複すると思いますが、備忘録も兼ねて説明的なものを書いてみます。
とあるマス$(i,j)$が選ばれた$K$個のマスを囲む長方形に含まれるようなマスの選び方は以下の通りに求められます。
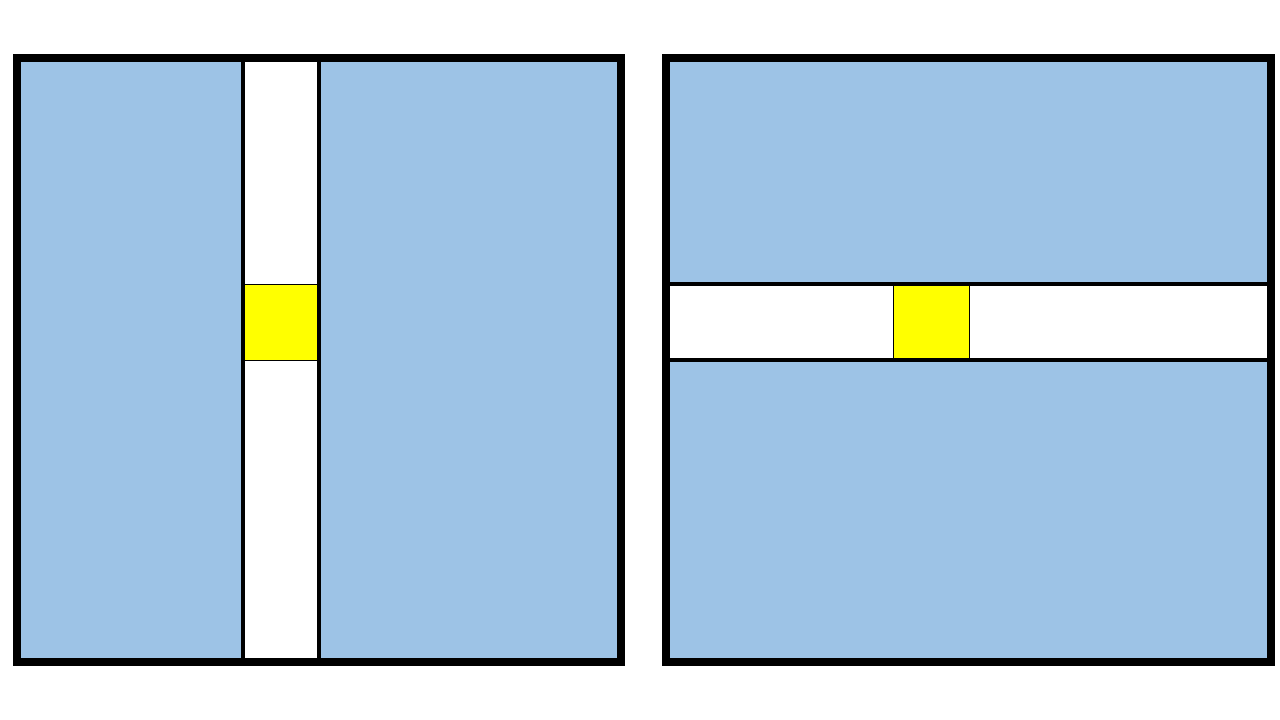
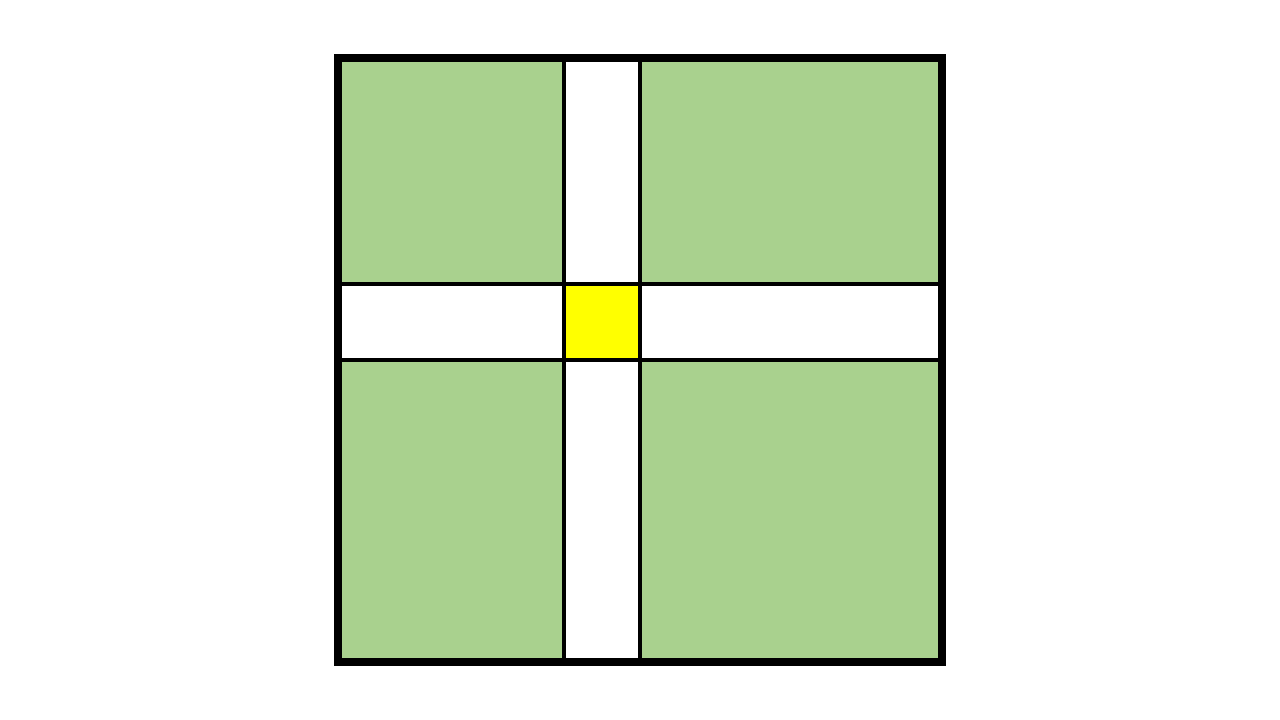
まず以下のような、$x$座標が$i$未満の範囲、$i$より大きい範囲、$y$座標が$j$未満の範囲、$j$より大きい範囲の4つの区域を考えます(青の部分)。
すると、各範囲内のみで$K$個のマスが選ばれた時は黄色のマスが長方形に含まれないと考えられます。ですので、全体から$K$個選ぶ通りから各範囲内で$K$個選ぶ通り数を引けば答えを求められそうですが、ただ範囲内での選び方を求めるだけでは以下の4つの範囲内のみで$K$個選んだ時の組み合わせを重複して求めていることになります(緑の部分)。
ですので、全体から$K$個選ぶ通りから各範囲内で$K$個選ぶ通り数を引いた後、この部分の選び方を再び加算してあげることで、$(i,j)$が選ばれた$K$個のマスを囲む長方形に含まれるようなマスの選び方を正しく求められます。
final class Main {
private static final boolean autoFlush = false;
private static final SimpleScanner sc = new SimpleScanner( System.in );
private static final SimplePrinter out = new SimplePrinter( System.out, autoFlush );
public static void main ( String[] args ) {
//H、W、Kの受け取り
int H = sc.nextInt();
int W = sc.nextInt();
int K = sc.nextInt();
//mod
final int mod = 998244353;
//階乗とその逆元を求めておく
Factorial fact = new Factorial(H*W,mod);
//答え用変数
long ans = 0;
//全マスからK個選ぶ通り数
long all = fact.getCombi(H*W,K);
//全マスに対して、そのマスが長方形に含まれる通り数を求める
for(int i=1;i<=H;i++){
for(int j=1;j<=W;j++){
//上記の各領域内でのK個選ぶ通り数を求める
long m1 = fact.getCombi(H*(j-1),K);
long m2 = fact.getCombi(H*(W-j),K);
long m3 = fact.getCombi((i-1)*W,K);
long m4 = fact.getCombi((H-i)*W,K);
long p1 = fact.getCombi((i-1)*(j-1),K);
long p2 = fact.getCombi((i-1)*(W-j),K);
long p3 = fact.getCombi((H-i)*(j-1),K);
long p4 = fact.getCombi((H-i)*(W-j),K);
//全通りから(i,j)が選ばれないマスの選び方を引いたものを加算
long sub = p1-m1+p2-m2+p3-m3+p4-m4;
ans += all+sub;
ans %= mod;
}
}
//負の値になっている可能性があるのでその時はmodを加算
if(ans<0)
ans += mod;
//ansを全通り数で割って出力
out.println(ans*MathFunction.modPow(all,mod-2,mod)%mod);
out.close();
}
}
全然思いつかなかった…。
G - Constrained Nim 2
問題文はこちら
公式解説の通りです。
final class Main {
private static final boolean autoFlush = false;
private static final SimpleScanner sc = new SimpleScanner( System.in );
private static final SimplePrinter out = new SimplePrinter( System.out, autoFlush );
public static void main ( String[] args ) {
//N、L、Rの受け取り
int N = sc.nextInt();
int L = sc.nextInt();
int R = sc.nextInt();
//grundy数の排他的論理和を求める
int now = 0;
while(N-->0){
int A = sc.nextInt();
now ^= (A%(L+R))/L;
}
//0より大きいなら先手が勝ち、0なら後手が勝つ
out.println(now>0?"First":"Second");
out.close();
}
}
grundy数を知らなかったので勉強になりました。
感想
A,B,C:易しい
D:そんなにループ回数が多くないことに気付いてからはサクッと解けた
E:特に何も考えずに提出してみたら通った
F,G:わかりません…
って感じでした。
Eまでは早く解けましたが、ちょっと難しくなると一気に手が出なくなってしまいますね…。精進不足な部分が露呈したような感じでした。