scipy.optimizeで、十種競技の世界記録を出すための最適解を算出

はじめに

「十種競技」という競技をご存知でしょうか？
2日間で走（100m, 400m, 1500m, 110mH）、跳（走高跳, 棒高跳, 走幅跳）、投（砲丸投, 円盤投, やり投）の10種目を行い、各種目の記録を得点化しその合計記録で争うという競技です。
現在(2020年6月)の世界記録は Kevin MAYER 選手の9126点です。

ところで、この点数を効率良く出すためにはどうすればいいでしょうか？
「全ての種目で均等に得点を取る」という考えがありそうですが、これは現実的ではありません。
種目によって得点を稼ぎやすいもの、稼ぎにくいものがあるためです。
例えば、各種目で900点を獲得するための記録は下記となります。
（参考までに、十種競技の種目ごとの日本記録も併載）

	100m	400m	1500m	110mH	走高跳	棒高跳	走幅跳	砲丸投	円盤投	やり投
900点	10.82	48.19	247.42	14.59	2.10	4.97	7.36	16.79	51.40	70.67
十種種目ごと日本記録	10.53	47.17	248.24	13.97	2.16	5.30	7.65	15.65	50.23	73.82

砲丸投か円盤投で900点を出すためには、日本記録を越えなければいけません。
これは現実的ではありませんね。

では、どうしたら最も簡単に世界記録を出せるでしょうか？
砲丸投では800点しか取れない代わりに他の種目で1000点取ろう、でも100mと1500mのどちらで1000点取るのが楽かなんて分からない…

この問いに対して私が出した答えは
「スコアリングテーブル（通称ハンガリアンテーブル）」**での総得点の最小値」**というものです。

#スコアリングテーブルとは？
国際陸上競技連盟（IAAF）が作成している各種目の記録を得点化した表で、十種競技とは計算式が異なります。
こちらは種目ごとの比較のために作られているので、「自分が出した100m 11.00(886p)という記録は、走幅跳だと6m83(886p)相当だな」などというように使用できます。

#算出したもの
「10種目のスコアの最小値（制約：十種の記録が9126点を超える）」を算出しました。

例えば、100mと砲丸投の2種目で合計1000点を目指すとします。
それぞれの種目で500点を出した時の合計スコアは972pですが、
100m14.00, 砲丸投13.32の時の合計スコアは945pであり、得点は同じでもこちらの方が楽に点数を稼げそうです。
（実際問題はまた別ですが……）

	記録	十種得点	スコア	:	記録	十種得点	スコア
100m	12.82	500	430	:	14.00	312	221
砲丸投	10.24	500	542	:	13.32	687	724
合計		1000	972	:		1000	945

このような感じで、いかに小さいスコアで世界記録を出せるかというのを求めています。

#算出方法
最適化手法は、scipy.optimizeのminimizeを使用しました。

記録の範囲は、スコア1p〜世界記録としました。
(トラック種目は下限が世界記録、フィールド種目は上限が世界記録です)

	100m	400m	1500m	110mH	走高跳	棒高跳	走幅跳	砲丸投	円盤投	やり投
下限	9.58	43.03	206.00	12.80	0.92	1.16	2.51	1.00	1.57	1.59
上限	16.79	78.01	380.04	25.43	2.45	6.18	8.95	23.12	74.08	98.48

十種競技の得点計算式はWikipediaに記載されています。
スコアリングテーブルの計算式は公式で見つけることができませんでしたが、下記の計算式で算出されるようです。

a × (記録 + b)^2 + c
（係数は下記に記載）

意外とシンプルですね。

以下、算出で使用したコマンドです。

import numpy as np
import pandas as pd
import copy
import sys
from scipy.optimize import minimize, BFGS, LinearConstraint, Bounds
from math import floor
import matplotlib.pyplot as plt

## スコアリングテーブル用係数
w_score = np.array([
    [24.64221166,-16.99753156,-0.218662048], #100m
    [1.021013043,-78.99469306,0.0029880052], #400m
    [0.0406599253,-384.9950051,0.001205591], #1500m 
    [7.665206128,-25.79302259,0.0141087786], #110mH
    [32.14570816,11.59368894,-5026.080842],  #HJ
    [3.045719921,39.33586031,-4993.213828],  #PV
    [1.931092873,48.34861905,-4993.807793],  #LJ
    [0.0423461436,684.8281542,-19915.72457], #SP
    [0.0040063129,2232.983411,-20003.52492], #DT
    [0.0024031525,2879.797864,-19950.96836]])#JT

## 十種競技用係数
w_dec = np.array([
    [25.4347,18,1.81],   #100m
    [1.53775,82,1.81],   #400m
    [0.03768,480,1.85],  #1500m
    [5.74352,28.5,1.92], #110mH
    [0.8465,75,1.42],  #HJ
    [0.2797,100,1.35], #PV
    [0.14354,220,1.4], #LJ
    [51.39,1.5,1.05],  #SP
    [12.91,4,1.1],     #DT
    [10.14,7,1.08]])   #JT

## 目的関数（スコアリングテーブル）
def calc_score(x):
    total_score = 0
    for i in range(10):
        total_score += w_score[i,0] * (x[i] + w_score[i,1])**2 + w_score[i,2]
    return total_score

## 制約関数（十種競技得点）
def calc_dec(x):
    n = 0
    total_point = 0
    target_point = 9126

    for i in range(10):
        if i in (0,1,2,3):
            total_point += w_dec[i,0] * (w_dec[i,1] - x[i]) ** w_dec[i,2] #100m, 400m, 1500m, 110mH
        elif i in (4,5,6):
            total_point += w_dec[i,0] * (x[i] *100 - w_dec[i,1]) ** w_dec[i,2] #走高跳, 走幅跳, 棒高跳
        else:
            total_point += w_dec[i,0] * (x[i] - w_dec[i,1]) ** w_dec[i,2] #砲丸投, 円盤投, やり投
        return_point = total_point - target_point
    return return_point

bounds = Bounds(world_rec[0:4] + min_rec[4:10] , min_rec[0:4] + world_rec[4:10])

cons = (
    {'type': 'ineq', 'fun': calc_dec} 
)

x0 = np.array([10, 46.19, 247.42, 13.59, 1.8, 3.5, 6.06, 10.79, 31.40, 53.67]) # 初期値は適当

関数の作成以外、ほとんど記載していません。
これだけで最適化問題を解けるなんて、とても簡単ですね…

#結果
##１．世界記録（9126点）達成時の最小スコア

result = minimize(calc_score, x0, constraints=cons, method="SLSQP", bounds=bounds)
print(result)
#     fun: 8707.88035324152
#     jac: array([-141.92468262,  -27.99401855,   -5.38891602,  -70.75549316,
#        902.8885498 ,  277.25720215,  221.29797363,   59.95800781,
#         18.4855957 ,   14.31445312])
# message: 'Optimization terminated successfully.'
#    nfev: 569
#     nit: 38
#    njev: 34
#  status: 0
# success: True
#       x: array([ 14.11782497,  65.28575996, 318.7265988 ,  21.17765192,
#         2.45      ,   6.18      ,   8.95      ,  23.12      ,
#        74.08      ,  98.48      ])

100m:14.11
400m:65.28
1500m:318.72
110mH:21.72
走高跳:2.45（世界記録）
棒高跳:6.18（世界記録）
走幅跳:8.95（世界記録）
砲丸投:23.12（世界記録）
円盤投:74.08（世界記録）
やり投:98.48（世界記録）

総スコア:8707

という結果となりました！ww
得点は指数関数的に増加するので、伸び率の高いフィールド種目を頑張れば
トラック種目は適当でも世界記録出るってことですかね………

##2.日本記録（8308点）達成時の最小スコア
世界記録だけだとつまらないので、日本記録バージョンも実行してみました。
なお、上限は「十種競技種目ごと日本記録」としました。

#結果のみ記載
result = minimize(calc_score, x0, constraints=cons, method="SLSQP", bounds=bounds)
print(result)
#     fun: 8397.295007256867
#     jac: array([-262.33532715,  -58.31018066,   -7.70007324, -130.22009277,
#        884.24414062,  271.89660645,  216.27709961,   59.32495117,
#         18.29467773,   14.19604492])
# message: 'Optimization terminated successfully.'
#    nfev: 521
#     nit: 30
#    njev: 30
#  status: 0
# success: True
#       x: array([ 11.67464597,  50.4396491 , 290.30574658,  17.29878908,
#         2.16      ,   5.3       ,   7.65      ,  15.65      ,
#        50.23      ,  73.82      ])

100m:11.67
400m:50.43
1500m:290.30
110mH:17.29
走高跳:2.16（十種日本記録）
棒高跳:5.30（十種日本記録）
走幅跳:7.65（十種日本記録）
砲丸投:15.65（十種日本記録）
円盤投:50.23（十種日本記録）
やり投:73.82（十種日本記録）

総スコア:8397p

という結果となりました。
フィールド競技で得点を稼ぐという傾向は変わりませんね…
ちなみに、右代選手が日本記録を出した際のスコアは8609pなので、
上記だと約200p効率良く日本記録を出せることになりますw

#おまけ
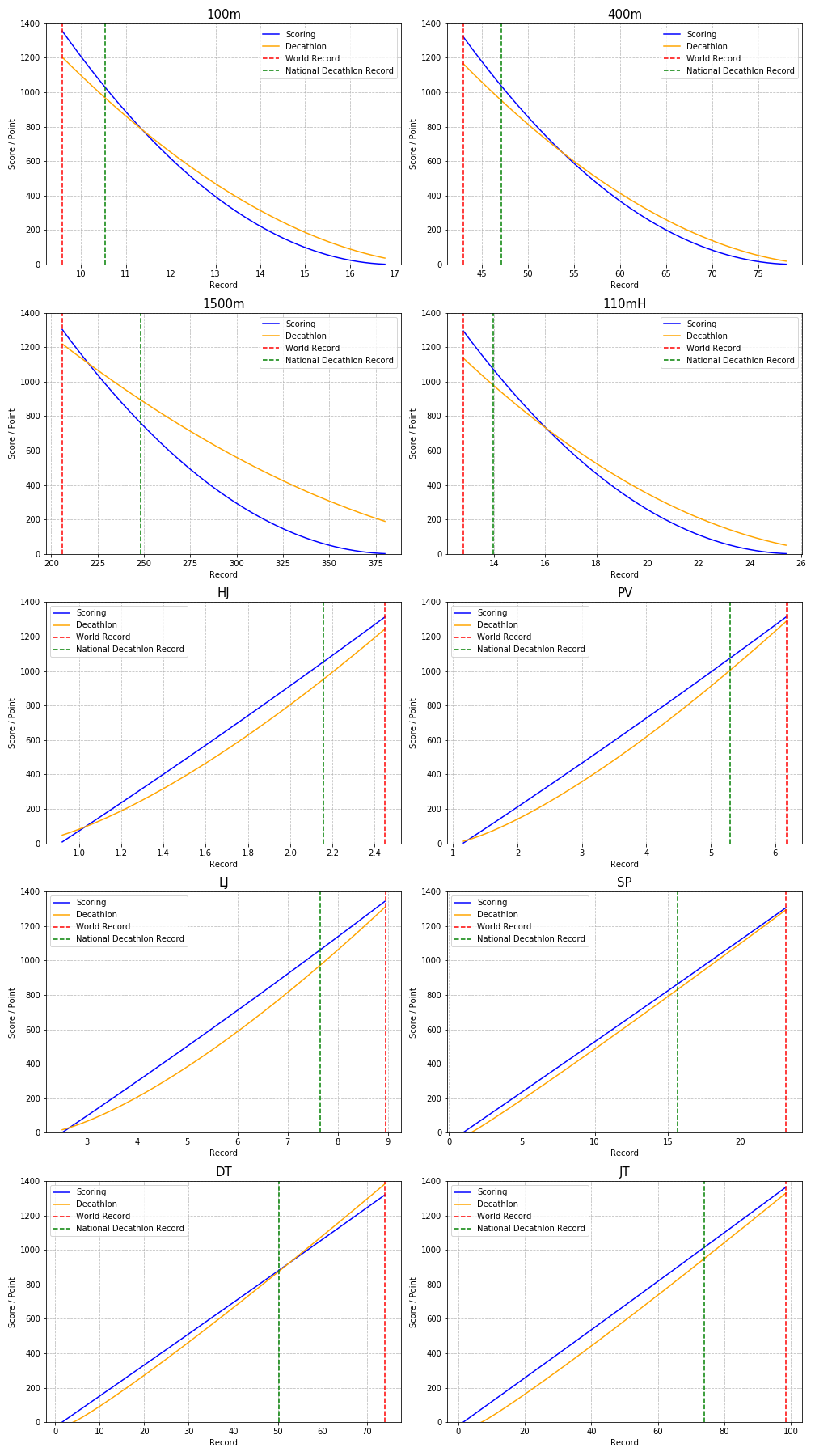
scipyとは関係ありませんが、十種競技の得点とスコアリングテーブルの計算式をグラフ化してみました。

## グラフ出力
fig, ax = plt.subplots(5, 2, figsize=(14, 25)) 

for i in range(10):
    pltx = np.arange(min(min_rec[i],world_rec[i]), max(min_rec[i],world_rec[i]), 0.01)
    plty = w_score[i,0] * (pltx + w_score[i,1])**2 + w_score[i,2]
    if i in (0,1,2,3):
        plty_p = w_dec[i,0] * (w_dec[i,1] - pltx) ** w_dec[i,2] #100m, 400m, 1500m, 110mH
    elif i in (4,5,6):
        plty_p = w_dec[i,0] * (pltx *100 - w_dec[i,1]) ** w_dec[i,2] #走高跳, 走幅跳, 棒高跳
    else:
        plty_p = w_dec[i,0] * (pltx - w_dec[i,1]) ** w_dec[i,2]
    
    ax[i//2, i%2].set_ylim([0,1400])
    ax[i//2, i%2].plot(pltx, plty, color="blue", label="Scoring")
    ax[i//2, i%2].plot(pltx, plty_p,color="orange", label="Decathlon")
    ax[i//2, i%2].set_title(label[i], size=15)
    ax[i//2, i%2].set_xlabel('Record')
    ax[i//2, i%2].set_ylabel('Score / Point')
    ax[i//2, i%2].axvline(x=world_rec[i], ymin=0, ymax=100, ls="--", color="red", label="World Record")
    ax[i//2, i%2].axvline(x=national_dec_rec[i], ymin=0, ymax=100, ls="--", color="green", label="National Decathlon Record")
    ax[i//2, i%2].grid(which = "major", axis = "both", alpha = 0.8,
        linestyle = "--", linewidth = 0.8)
    ax[i//2, i%2].legend(loc='best')

plt.tight_layout()

高得点領域において、トラック種目はフィールド種目に比べてスコアに対する十種の得点が低い（=高スコアを出しても得点に反映されにくい）気がします。
「最小スコアで高得点を出すためにはフィールドで高スコアを出す」という結論に至った理由が分かるような気がします。。

#終わりに
scipy.optimizeは統計学ド素人の私でも使えました。とても便利…
本記事を通して気軽に最適化問題に取り組む人（&十種競技に興味を持った人）が増えれば幸いです。