先週の土日連続 ABC、この記事は日曜日の回です。Fが難問で、E完でした。
AtCoder Beginner Contest 128
- この連載記事では、着手した問題の考察を自分なりに書いていきます。
- 問題の詳細は問題一覧を参照してください。
A - Apple Pie
問題概要: A 個の林檎と、P 個の林檎の欠片がある。林檎1個から林檎の欠片を3個作れる。林檎の欠片2個からアップルパイを1個作れる。作れるアップルパイの個数の最大値を求めよ。
考察
アップルパイを作るには林檎の欠片が必要なので、作れる林檎の欠片の個数の最大値を求めればよいです。
林檎の欠片は、始めからある P 個に加えて、林檎を砕いて作れる 3A 個です。
したがって、floor((3A + P) / 2) 個のアップルパイを作れます。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc128/submissions/5639071
B - Guidebook
問題概要: レストランが N 個ある。i 番目のレストランは市 S(i) にあり、評価点が P(i) である。レストランの番号を以下の順番で出力せよ。
- 市名 S が小さい順
- 同じ市に複数のレストランがあるときは、評価点の高い順
考察
ソートする問題です。
SQL なら order by S asc, P desc と書くだけですが、言語/ライブラリのソート関数によっては、列ごとに asc/desc を指定することができないので、一定の工夫が必要です。
大きく分けて2通りの考え方があります。
- (市, 逆順(評価点), レストラン番号) というタプルをリストに入れてソートする
- 比較関数を自作してレストラン番号のリストをソートする
考察: タプルをソートする解法
std::cmp::Reverse (の自作版) を使って評価点の大小関係を逆順にすれば、タプルを辞書順でソートするだけになります。
レストランごとにタプルを作ってリストに詰めて、ソートすればよいです。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc128/submissions/5638835
考察: 比較関数を自作する解法
レストランの番号をリストに入れておき、番号の間の大小関係を定義する比較関数をソート関数に渡してソートする、ということもできます。
こちらの方が、値の詰め替えが発生しない上に、ソートされるリストの要素が小さいため、効率的です。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc128/submissions/5720463
C - Switches
問題概要: N 個のスイッチと M 個の電球がある。電球 i は1つ以上のスイッチと接続されていて、接続されているスイッチのうち on になっているものの個数の偶奇が P(i) のとき点灯する。すべての電球が点灯するスイッチの on/off の組み合わせを数えよ。
制約
- N, M ≤ 10
考察
N, M が小さいので、on/off の組み合わせを全探索すればよいです。
2値の組み合わせの全探索にはビット全探索というのを使うと簡単に書けます。(競プロ参戦記 #43 のB問題の考察 を参照)
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc128/submissions/5638020
D - equeue
問題概要: N 個の宝石が入った筒がある。i 番目の宝石は価値 V(i) である。筒の左端に宝石を入れる、左端の宝石を出す、右端に宝石を入れる、右端の宝石を取り出す、という4つの操作を合計で K 回まで行うとき、最終的に筒の外にある宝石の価値の合計の最大値を求めよ。
制約
- N ≤ 50
- K ≤ 100
考察
操作の順番として、価値のある宝石を取り出した後に、価値が負の宝石を左右どっちかに詰めていく、というのが最適です。
左から取り出す宝石の数、右から取り出す宝石の数、最後に捨てる宝石の数、という3つの変数を全列挙して、シミュレーションすればよいです。
N, K がとても小さいので十分に間に合います。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc128/submissions/5640974
E - Roadwork
問題概要: 1本の道路があり、道路工事の計画が N 個ある。i 個目の工事により、位置 X(i) は時刻 S(i) ≤ t < T(i) の間、通行止めになる。Q 人の人がいて、j 番目の人は時刻 D(j) に位置 0 から x 方向に速度 1 で歩き出し、通行止めになっている点に遭遇した時点で停止する。各人が停止するか判定し、停止するなら歩く距離を求めよ。
考察
歩く人と工事のペアを列挙すると TLE します。
実は、「j 番目の人が遭遇する通行止めの集合」をうまく計算することで、歩行距離を効率的に計算できます。
以下の言い換えをします。
- 位置 X が時刻 [S, T) で通行止めになる
- 時刻 [S - X, T - X) に歩き始める人は位置 X で通行止めに遭遇する
計算量を無視すれば、以下のような手順で解答できます。
- 通行止め地点からなる集合 Xs = {} とする
- 時刻 t = 0 から始めて1ずつ増やす
- 各 i につき
- t = S(i) - X(i) なら、通行止め地点の集合 Xs に X(i) を入れる (♠)
- t = T(i) - X(i) なら、通行止め地点の集合 Xs から X(i) を除去する (♣)
- 各 j につき
- t = D(j) なら、現在の通行止め地点の集合に含まれる最小値を人 j の歩行距離として出力する (♥)
これは明らかに TLE しますが、3つの操作 (♠) (♣) (♥) だけを抽出して処理すれば間に合います。
時刻と操作のペアをリストに入れて、時刻に関してソートし、前から順番に処理していけばよいです。
通行止め地点の集合としてヒープ (優先度つきキュー) を使えば、最小値は高速に計算できます。
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc128/submissions/5645218
読みやすく書き直したのがこちら: https://atcoder.jp/contests/abc128/submissions/5720200
F - Frog Jump
問題概要: 数直線があり、位置 0, 1, .., N-1 に蓮が1個ずつ置かれている。正の整数 A, B を適当に決めて、現在位置 x = 0 から始めて以下の操作を行うとき、得点の最大値を求めよ。
- 現在位置 x から y = x + A に移動する
- y = N-1 なら終了する
- 位置 y に蓮がなければ溺れる (得点を 10^100 減らして終了する)
- 位置 y の蓮を削除して得点を S(y) 増やす
- 現在位置 x から y = x - B に移動する
- 同様
考察
本番では全然分からなかったので解説生放送を聞いて実装しました。
まず具体的な A, B について試し、カエルの飛び先がどのようになるかを見ます。式で書くと、
0, A, A-B, A-B+A, A-B+A-B, ..
になります。A-B の値 (2回飛んだときの前進幅) が大事なので C = A-B で変換すると、
0, A, C, C+A, C+C, C+C+A, ..
つまり、
0, A, C, C+A, 2C, 2C + A, ..
となります。これは偶数番目と奇数番目で分けると分かりやすくて、
- 偶数番目: 0, C, 2C, 3C, .., kC
- 奇数番目: A, C+A, 2C+A, 3C+A, .., kC+A
となります。
カエルは最終的に x=N-1 に到達しなければいけませんが、 N-1 より先には蓮がないので戻るジャンプで N-1 に行くということはありません。そのため、ゴールするには整数 k が存在して
kC + A = N-1
となっている必要があります。C, k を決めると A, B の値が決まります。
- A = N - 1 - kC
- B = A - C = N - 1 - (k + 1)C
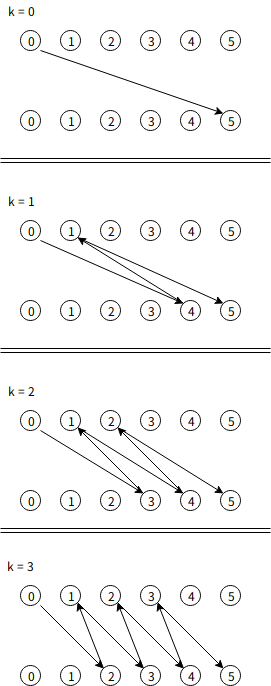
そろそろ具体例を見ます。N=6, C=1 は以下のようになります。(偶数番目と奇数番目を強調するために上下に分けていますが、上下の丸は同じ蓮です。)
このように k を大きくするたびに踏む蓮の集合が単調増加します。
この性質はとても嬉しくて、C を固定しながら k を 0 から増やしていくループを回すとき、得点の合計値や踏んだ蓮の集合を次の周に持ち越せるわけです。
計算量的にも問題ありません。kC + A = N-1 から k ≤ (N-1)/C がいえるので、(C, k) を列挙する2重ループの計算量は多めに見積もっても N + N/2 + N/3 + .. + N/N = O(N log N) となります。(調和級数)
筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc128/submissions/5693867