競プロ参戦記 #55 Rain Flows into Dams | ABC 133

ABC-only 回です。参加できなかったので練習記になります。D に90分ぐらい費やしていたので実質C完でした。

AtCoder Beginner Contest 133

• この連載記事では、着手した問題の考察を自分なりに書いていきます。
  • 前回: 競プロ参戦記 #54 Hopscotch Addict | ABC 132
• 問題の詳細は問題一覧を参照してください。
  • 問題一覧: https://atcoder.jp/contests/abc133/tasks

A - T or T

問題概要: N 人で旅行しようとしている。交通手段として電車とタクシーがある。電車を使うと、1 人あたり A 円のかかる。タクシーを使うと、N 人で B 円かかる。交通費の最小値を求めよ。

A: 考察

1人あたり A 円ということは N 人で N * A 円です。N * A と B の小さい方を出力すればよいです。

2つの数値の小さい方を計算する関数として std::cmp::min があります。

筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc133/submissions/6397873

B - Good Distance

問題概要: D 次元上に N 個の点がある。i 番目の点の座標を (X(i, 1), X(i, 2), .., X(i, D)) で表す。点のペアで、2点間の距離が整数であるようなものを数えよ。

制約:

• N≤10
• X(i, j): 整数

B: 考察

制約から点のペアは 100 通り以下です。これらを列挙して、ペアが実際に条件を満たすか判定する方針で考えます。

制約から点の座標は整数なので、2点間の距離の2乗 X は常に整数になります。X の平方根 (距離) が整数かどうかは、実際に r * r = X になる整数 r があるかを調べればよいです。

調べるのは r * r ≤ X の範囲で十分なので、全体として O(√X) 時間です。具体的には、制約から X < 10^9 が分かるので、10^5 ステップ程度です。

全体として 10^7 ステップ程度で解けます。

筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc133/submissions/6397954

C - Remainder Minimization 2019

問題概要: 非負整数 L, R が与えられる。条件 L ≤ i < j ≤ R をみたす整数 i, j について、式 (i * j) % 2019 の最小値を求めよ。

C: 考察

はじめに最小値 0 を達成できるか確認します。(i * j) % 2019 = 0 は要するに i * j が 2019 の倍数ということなので、i, j のどちらかを 2019 の倍数にすればよいです。

L, R の範囲が十分に広ければ (R - L > 2019)、2019 の倍数が含まれるので最小値 0 が達成可能です。

逆に R - L ≤ 2019 のケースでは、全探索すればよいです。

筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc133/submissions/6398035

D - Rain Flows into Dams

問題概要: 円周上にダムと山が交互に N 個ずつ存在する。i 番目の山に x リットルの雨が降った後、両隣のダムにそれぞれ x/2 リットルの水が溜まることが知られている。

i 番目のダムに溜まっている水の量を A(i) とおく。はじめ A(i) = 0 である。すべての山に雨が降った。これにより i 番目の山に降った雨の量を L(i) リットルとおく。このときの貯水量 A(i) が与えられる。

L(i) は一意に定まる。L(i) を求めよ。

制約:

• N: 奇数
• L(i): 偶数

D: 考察

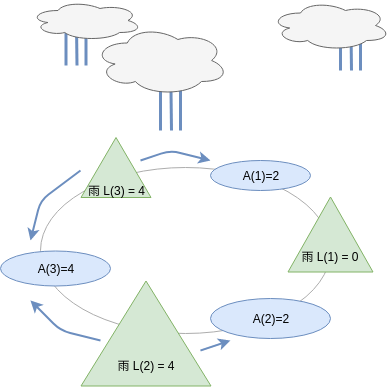
例えば N=3, A=(2, 2, 4) なら以下のように、降雨量がそれぞれ L=(4, 0, 4) になります。

各ダムの貯水量は両隣の山の降水量の半分の和なので、以下の連立方程式が立ちます。

• L(1)/2 + L(2)/2 = A(1)
• L(2)/2 + L(3)/2 = A(2)
• L(3)/2 + L(1)/2 = A(3)

変形すると、

• L(2)/2 = -L(1)/2 + A(1)
• L(3)/2 = -L(2)/2 + A(2)
• L(1)/2 = -L(3)/2 + A(3)

となります。

上の2本の式によれば L(2), L(3) はいずれも L(1) を使って表せます。そのため、3本目の式は L(1) 単独の一次方程式に変形可能です。それを解けば L(1) の値が判明して、残りの変数の値も計算できます。

方針が定まったので、次に実装です。変数 L(i) が L(1) の一次式で表すということは、以下の式を満たす s(i), t(i) (係数) を求めればいいです。

    L(i) = s(i) * L(1) + t(i)

i=1 では明らかに s(i)=1, t(i)=0 です。

一般に L(i+1) (ただし i+1≤N) については、

    L(i+1)/2 = -L(i)/2 + A(i)
    L(i+1)   = -L(i) + 2 * A(i)
             = -(s(i) * L(1) + t(i)) + 2 * A(i)
             = (-s(i)) * L(1) + (2 * A(i) - t(i))

    s(i+1) = -s(i)
    t(i+1) = 2 * A(i) - t(i)

となります。最後の式だけは L(i), L(i+1) ではなく L(N), L(1) に関する式なので一般化できませんが、

    L(N) = s(N) * L(1) + t(N)

    L(1)/2 = -L(N)/2 + A(N)
    L(1)   = -L(N)   + 2 * A(N)
           = -(s(N) * L(1) + t(N)) + 2 * A(N)
           = (-s(N)) * L(1) + (2 * A(N) - t(N))

    (1 + s(N)) * L(1) =  2 * A(N) - t(N)
                 L(1) = (2 * A(N) - t(N)) / (1 + s(N))

というふうになります。(N が奇数という制約のおかげで 1 + s(N) ≠ 0 (= 2) がいえます。)

というわけで DP で解けました。

筆者の回答 (Rust, AC): https://atcoder.jp/contests/abc133/submissions/6399196

Weighted Union Find を使おうとしましたがいりませんでしたね……