Trilinear interpolation
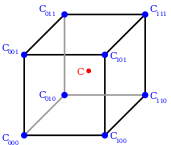
Suppose the following cube,
which cube has eight vertexes, $c_{000},c_{100},c_{010},c_{110}c_{001},c_{101},c_{011}$ and $c_{111}$ at
$\left(x_{0,}y_{0},z_{0}\right),\left(x_{1,}y_{0},z_{0}\right),\left(x_{0,}y_{1},z_{0}\right),\left(x_{1,}y_{1},z_{0}\right),\left(x_{0,}y_{0},z_{1}\right),\left(x_{1,}y_{0},z_{1}\right),\left(x_{0,}y_{1},z_{1}\right)$ and $\left(x_{1,}y_{1},z_{1}\right)$ respectively, and suppose there is a vertex $c$ at $\left(x,y\right)$ is contained within the cube.
Normalized distances $x_{d}$,$y_{d}$ and $z_{d}$ is defined as follows:
$$
\begin{align}
x_{d} &= \left(x-x_{0}\right)/\left(x_{1}-x_{0}\right),\
y_{d} &= \left(y-y_{0}\right)/\left(y_{1}-y_{0}\right),\
z_{d} &= \left(z-z_{0}\right)/\left(z_{1}-z_{0}\right).
\end{align}
$$
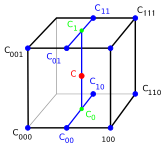
Linear interpolation $c_{00},c_{01},c_{10},c_{11}$of $c_{000}$ and $c_{100}$,$c_{001}$ and $c_{101}$, $c_{010}$ and $c_{110}$, $c_{011}$ and $c_{111}$ are defined as follows:
\begin{align}
c_{00} &= c_{000}\left(1-x_{d}\right)+c_{100}x_{d},\\
c_{01} &= c_{001}\left(1-x_{d}\right)+c_{101}x_{d},\\
c_{10} &= c_{010}\left(1-x_{d}\right)+c_{110}x_{d},\\
c_{11} &= c_{011}\left(1-x_{d}\right)+c_{111}x_{d}.
\end{align}
Bilinear interpolation $c_{0},c_{1}$ of $c_{00}$ and $c_{10}$, $c_{01}$ and $c_{11}$ are defined as follows:
\begin{align}
c_{0} &= c_{00}\left(1-y_{d}\right)+c_{10}y_{d},\\
c_{1} &= c_{01}\left(1-y_{d}\right)+c_{11}y_{d}.
\end{align}
Trilinear interpolation $c$ of $c_{0}$ and $c_{1}$ is defined as follows:
$$c = c_{0}\left(1-z_{d}\right)+c_{1}z_{d}.$$
Above equation is able to be expand as follows:
\begin{align}
c &= &c_{0}\left(1-z_{d}\right)+c_{1}z_{d}\\
&= &\left(c_{00}\left(1-y_{d}\right)+c_{10}y_{d}\right)\left(1-z_{d}\right)+\left(c_{01}\left(1-y_{d}\right)+c_{11}y_{d}\right)z_{d}\\
&=&\left(\left(c_{000}\left(1-x_{d}\right)+c_{100}x_{d}\right)\left(1-y_{d}\right)+c_{10}y_{d}\right)\left(1-z_{d}\right)+\\
& &\left(\left(c_{001}\left(1-x_{d}\right)+c_{101}x_{d}\right)\left(1-y_{d}\right)+c_{11}y_{d}\right)z_{d}\\
&=&c_{000}\left(1-x_{d}\right)\left(1-y_{d}\right)\left(1-z_{d}\right)+\\
& &c_{100}x_{d}\left(1-y_{d}\right)\left(1-z_{d}\right)+\\
& &c_{010}\left(1-x_{d}\right)y_{d}\left(1-z_{d}\right)+\\
& &c_{110}x_{d}y_{d}\left(1-z_{d}\right)+\\
& &c_{001}\left(1-x_{d}\right)\left(1-y_{d}\right)z_{d}+\\
& &c_{101}x_{d}\left(1-y_{d}\right)z_{d}+\\
& &c_{011}\left(1-x_{d}\right)y_{d}z_{d}+\\
& &c_{111}x_{d}y_{d}z_{d}.
\end{align}
Matrix notation is also able to be written as follows:
c = \left[\begin{array}{cccccccc}
c_{000} & c_{100} & c_{010} & c_{110} & c_{001} & c_{101} & c_{011} & c_{111}\end{array}\right]\left[\begin{array}{c}
\left(1-x_{d}\right)\left(1-y_{d}\right)\left(1-z_{d}\right)\\
x_{d}\left(1-y_{d}\right)\left(1-z_{d}\right)\\
\left(1-x_{d}\right)y_{d}\left(1-z_{d}\right)\\
x_{d}y_{d}\left(1-z_{d}\right)\\
\left(1-x_{d}\right)\left(1-y_{d}\right)z_{d}\\
x_{d}\left(1-y_{d}\right)z_{d}\\
\left(1-x_{d}\right)y_{d}z_{d}\\
x_{d}y_{d}z_{d}
\end{array}\right].