【Unity , shader】原神の海を再現したい

BGMが良いと話題になってた原神を最近やってみたのですが、グラフィックすごい感動したので作りたくなった

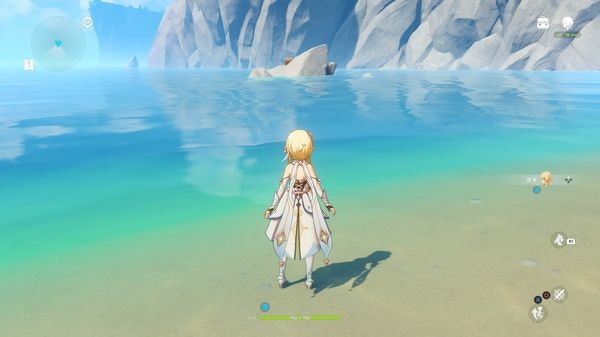
これがスタート地点の海なんですが、もうすごい
海、メチャクチャ良いな～となって、海のシェーダを書いてみました。
できたものがこちら

きれいな海ができました！
追記:シェーダのコードはこちらになります https://github.com/Uynet/Gensin-Sea/blob/main/Assets/Scenes/sea.shader

今回はこちらの作り方を紹介します。それでは....
えいっ

まず適当に2枚の板を交差させました。これが海と浜になります。

深度値によるグラデーション

浅瀬から沖にかけてのエメラルドグリーンのグラデーションが非常によいですね。
見た感じ水の層の厚さで色が変化しているように見えます。

カメラから見た海と浜の深度値の差を取り深さを計算してみます。

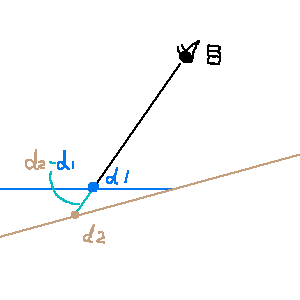
d1 ... カメラ位置から水面までの距離
d2 ... カメラ位置から地面までの距離

d1はComputeScreenPosとCOMPUTE_EYEDEPTHを使って取得できます。
d2は深度テクスチャを使用し取得します。

実装はこの記事を参考にすると良いです。
http://tips.hecomi.com/entry/2018/09/15/014050

d2-d1で水の層の厚さが計算できるのでいいかんじのグラデーションを当ててみます。
また浅くなるほど色が薄くなるはずなので、深度でアルファブレンドをかけてあげます。

木の棒は立体感を出したくて適当に置きました
海っぽくなりましたね

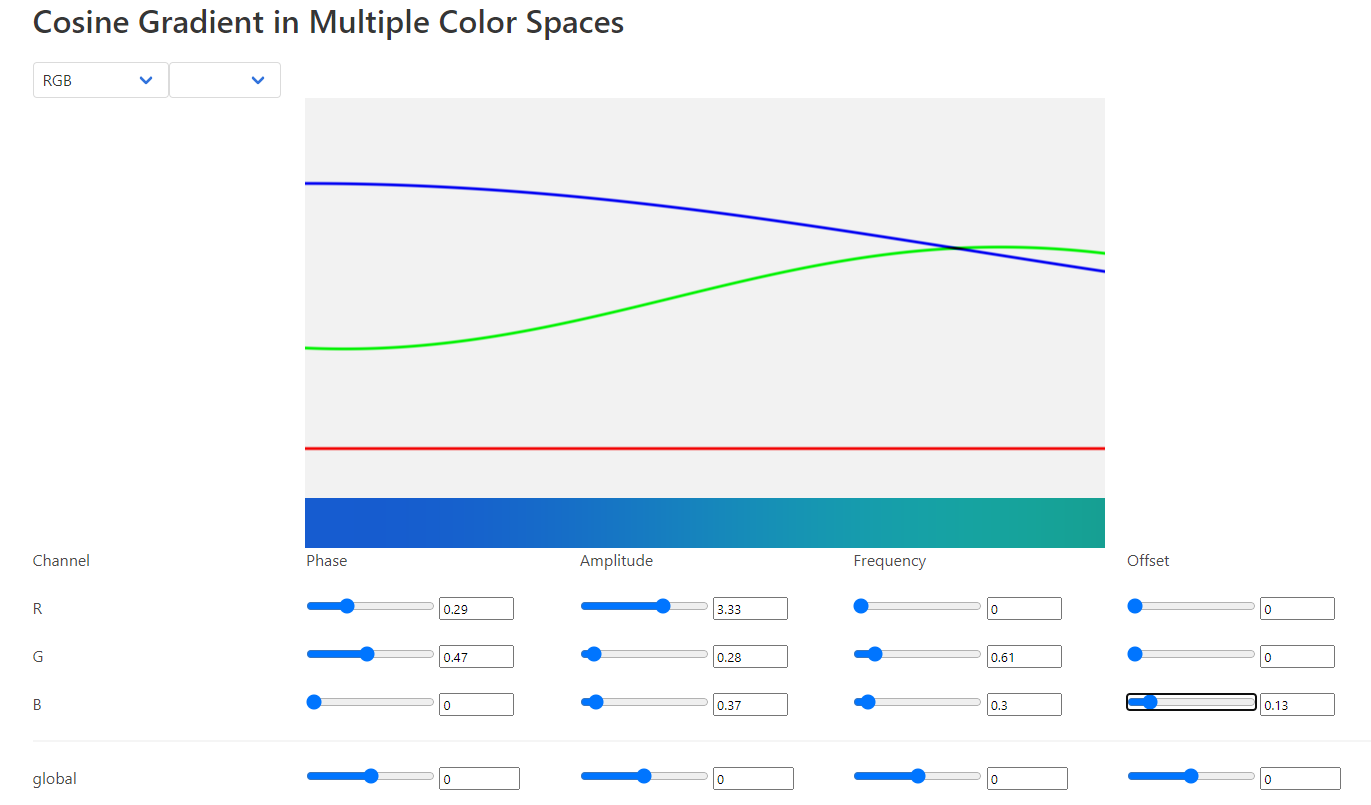
ちなみに、シェーダでいい感じのグラデーションを作る時に便利なサイトを紹介します。
https://sp4ghet.github.io/grad/

RGBそれぞれのsin波のパラメータをいじって君だけのグラデーションを作ろう！というサイトです。
作ったパラメータはGLSLで書き出せるようなので、手打ちでHLSLに変換するとUnityに使えます。

ちなみに沖縄のような不純物が少なく透き通った海でこのグラデーションが見られるみたいです
今回やってないですが、光の波長ごとの散乱についてもっと厳密なモデルを用意するとちゃんと計算できそう感はありますね。

水面の反射

空が海に反射して映り込む感じにします。
その前にskyboxを貼ります。フリーで良さそうなアセットをお借りしました。
Fantasy Skybox FREE

skyboxを貼ったら反射による空の映り込みを計算してみます。¹

// relfection color
half3 reflDir = reflect(-viewDir, normal);
fixed4 reflectionColor = UNITY_SAMPLE_TEXCUBE_LOD(unity_SpecCube0, reflDir, 0);

viewDir...視線ベクトル
normal...水面の法線ベクトル
unity_SpecCube0 .. skyboxのテクスチャ²

やってることは視線ベクトルを水面で反射させskyboxから色を取得しているだけです。

あと、砂浜にテクスチャを貼ってみました。かなり見た目がよくなります。
textures.comというサイトで無料の物がいくつか手に入るのでそれを使ってます。

フレネル反射率の計算

水面を真上から見ると透き通って見えるけど水平近くから見ると結構反射して見える、フレネル反射という現象があります。
フレネル反射率の計算にあたりSchlickの近似と呼ばれる近似モデルがあるので、こちらを計算してみます。

F_{r}(\theta) = F_0 + (1 - F_0)(1-cos\theta)^5

$ F_r(\theta) $ ... 入射角$\theta$で入射する光の反射率
$ F_0 $ ... 入射角$\theta$が0の時、つまり真上から入射したときの反射率
$ \theta $ ... 入射角

cosθは光の入射ベクトルと水面の法線ベクトルの内積によって計算できます。
これできれいな水面の反射ができました！
これでもウユニ塩湖みたいできれいですが、海っぽく波打たせてみましょう

水面ゆらがせる

パーリンノイズの生成

画像:wiikpedia

自然的なCG表現をするに当たってよく使われるアルゴリズムです。これを使い海をうねうねさせてみます。
用意されたテクスチャを使う方法もあるのですが、動かしたかったのでパラメトリックに生成できるものを使います

実装に当たってこちらの記事を参考にしました。
空の缶詰

法線の計算

生成したノイズをハイトマップとして扱い、この結果から法線を計算します。
意外と簡単で、x方向、y方向それぞれの勾配を計算しその外積を取ります。
hlslにはddx,ddyという、隣のピクセルとの差分を取得できる関数があるのでそれを使いましょう。

参考:マルペケつくろーどっとコム

normal = cross ( 
    float3(0,ddy(height),1),
    float3(1,ddx(height),0)
)

計算した法線を使って鏡面反射を計算してみます。

いい感じにうねうねしてくれました！
しかし遠くの方がけっこう気持ち悪いことになってます。
この現象はエイリアシングと呼ばれ、スクリーン上で波の密度が高くなりすぎると発生します。

エイリアシングの解決

嘘っぽくなりますが、水平線近くの方でハイトマップの値を抑えればよさそうです。

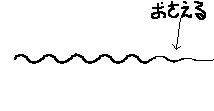
では水平線の近く、をどう計算すればよいでしょうか？
次のようなしましま模様を斜めから眺めることを考えます。

すると画面ではこんな映り方をするはずです。

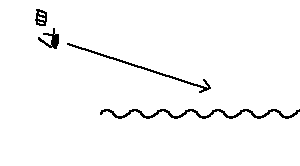
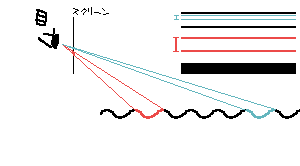
近くの波(赤)では画面上で広く、遠くの波(青)は画面上で狭く映ります。
この波の一周期ぶんはスクリーンでどれくらいの大きさになるか？を計算したいです。そこで、hlslの微分演算子を使えることを利用して、**画面上で一つ上のピクセルに移動すると、対応する水面上の点はどれだけ奥に移動するか？**を計算することを考えます。³

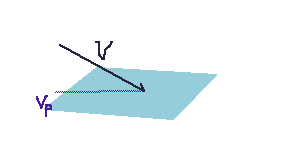
カメラから水面上の点に向かうベクトル$V$の水平面への射影$V_p$の大きさの微分を取ってみます。
水面を座標軸に水平なものと限定すると、$Vp = Vx + Vz$　なので、

ddy(length ( v.xz ))

となります。
この値を出力するとこのような感じになります。(そのままだと真っ白になるので調整してます)

この白くなってる所でエイリアシングが発生してそうなので、この値をいい感じの指標として波を抑えてみました。

良さそうですね。本当は厳密にどの周波数からエイリアシングを起こすかちゃんと計算したほうがいいですが、大変なのでやりません。
適切な指標としていい感じに扱えればまあ大丈夫そうです。

完成

出来上がりです。
パーリンノイズの値をUVスクロールすることでいい感じに波っぽく動かしてみました。

こうしてただの二枚の板が海になりました。
他にも水底のコースティクスとか、水に入ると白波のインタラクションを起こすとか、水の屈折を追加するとか色々やってみたいな～という事があるのでまた続きを書くかもしれません。
VRChatとかに公開できたらいいですね

リポジトリ : https://github.com/Uynet/Gensin-Sea
シェーダ : https://github.com/Uynet/Gensin-Sea/blob/main/Assets/Scenes/sea.shader

1. この方法では周囲のskymapから取得しているだけなので、周辺に物体があったときの映り込みなどは描画されません。そういうことがしたい場合はReflection Probeを生成すると良いです。また、明るさの調整が上手くいかなかったのでspecular光は実装していません。 ↩

2. Reflection Probeが存在し、その影響範囲内である場合はそのキューブマップが指定されます。 ↩

3. 今回簡易的にy方向の微分しか取っていませんが、例えば砂浜に寝転がったようなアングルではエイリアスがx軸方向に発生することも考えられるため、ちゃんとやるにはxy方向両方での微分を考える必要があるかもしれません... ↩