1/23にドワンゴからの挑戦状というdwango主催のコンテストの予選があったのですが、それのE問題について終了後に考えた解法について書きます。
問題概要
問題を意訳すると、
- $n$要素の$(t_i,p_i)$の列が与えられるので、広義昇順の数列$\{u_n\}$で$\sum_i |u_i-p_i|$を最小化するときの最小値を求めよ。ただし$\{t_n\}$は広義昇順で、$n\le 10^5$である。また、$t_i=t_{i+1}$ならば、$u_i=u_{i+1}$でなければならない。
という感じです。
この問題は、過去にも何度か類題が出ていて、本番ではそのときの回答を流用して解けましたが、どうやらその方法は効率が悪かったようです。で、少し考えたらこんな感じでいいんじゃない?という解法が生えたので書きたいと思います。解いた他の人達はSegmentTreeを使っていたんですがここでは触れません。
適当なシミュレーション
たとえば次のケースを考えます。
5 1000
1 5
2 8
6 6
9 1
9 4
先頭から$\{u_n\}$を決めていきます。$f_k = \sum_{i=1}^k |u_i-t_i|$として、$f_1$の分布は$|u_1-t_1|=|u_1-5|$になります。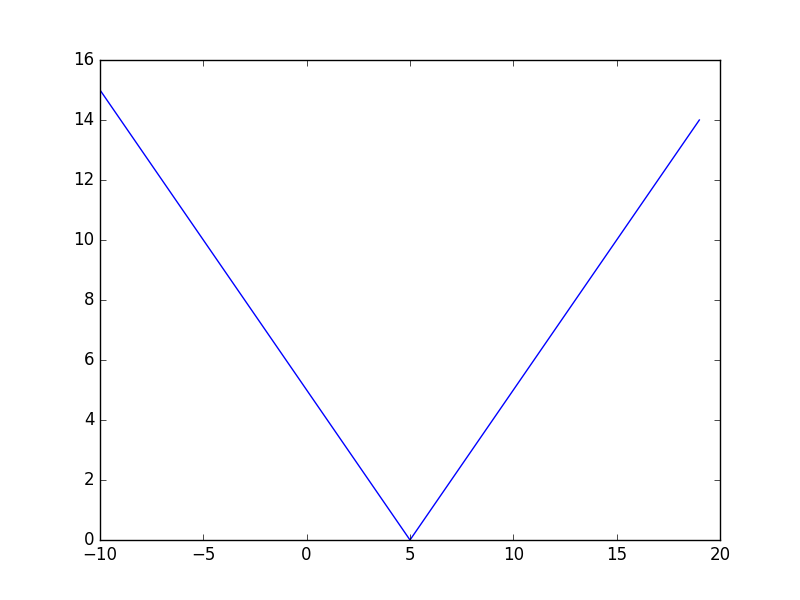
つぎに8を加えるわけですが、2項目単体でみると$|u_2-8|$になり、やはり上と似た概形になります。ただ$\{u_n\}$は広義昇順なので、$u_1$は$u_2$以下でなければなりません。そこで$u_2$が与えられた時、$u_1$でのグラフで$u_2$の位置より左側で最小の値を選ぶとすると、グラフは次のようになります。5以上の範囲の値が0になっています。
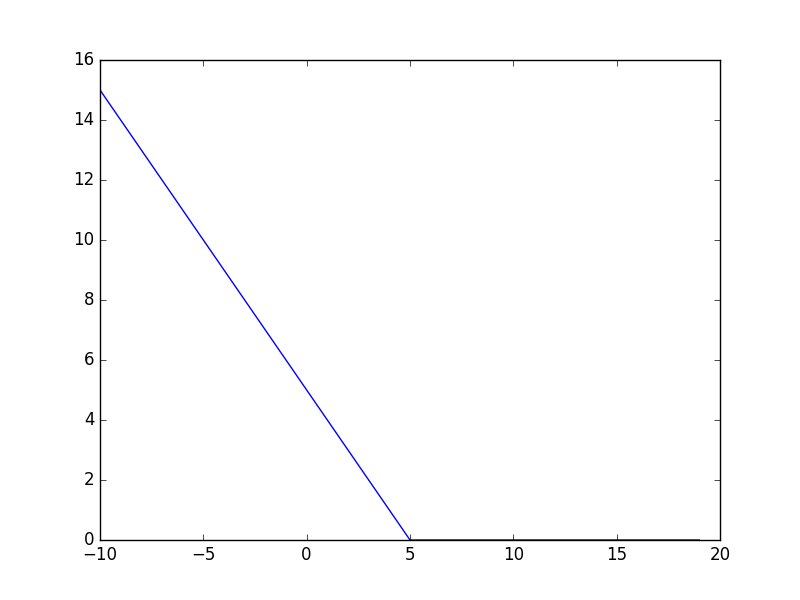
これに$|u_2-8|$を足して$f_2$のグラフが次のようになります。これは$u_2$の値についてそれぞれとりうる和の最小値を求めてそれをつないでグラフにしているのと同様です。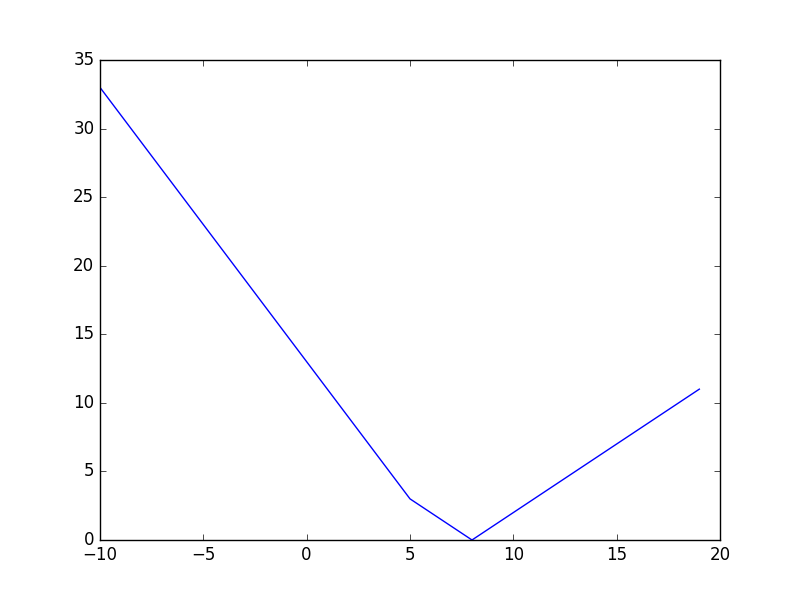
$f_2$の最小値は0で$u_2=8$のときにそうなります。
同様に$f_3$について行いましょう。各位置について左側をみたときの最小値のグラフは次のようになって、
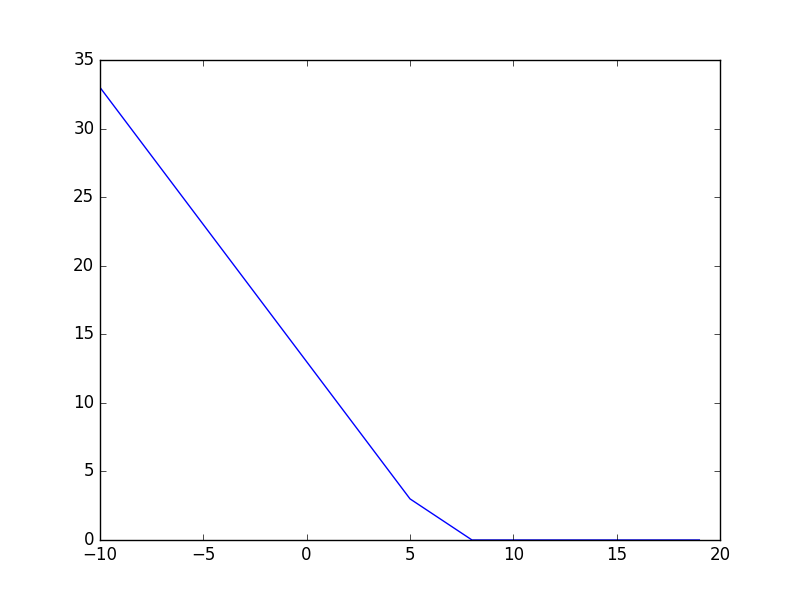
これに$|u_3-6|$を足して、
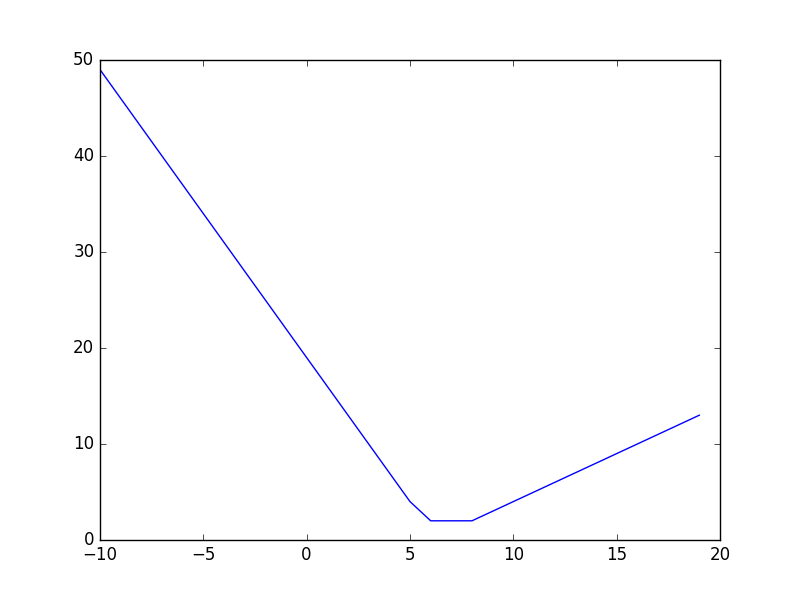
こんな感じになります。$f_3$の最小値は2で、$u_3\in [6,8]$のときにそうなります。
$f_4,f_5$も同様にやりますが、$t_4=t_5$なので、$u_4=u_5$でなければなりません。左側をみたときの最小値をとってから、$|u_4-1|$と$|u_5-4|$をいっぺんに足せば良いです。
解法
さて、上に出てきたグラフですが、結構単純なつくりになっています。
- 折れ線である。
- 折れ線の構成要素の傾きは整数で、単調増加している
- 左端の要素の傾きは、要素を1個くわえるごとに1ずつ下がっている。
- 傾きが変わる点は$p_i$にしかない。
$f_1$のグラフは、5の点で傾きが+2されていると考えることも出来ます。そして左側最小化によって5の点で傾きが+1にかわり、$|u_2-8|$をたすことにより、8の点で傾きを+2する…
傾きを+1する作用を持つ位置を昇順に並べてみると次のように遷移します。
$[5,5]\to [5]\to [5,8,8]\to [5,8]\to [5,6,6,8]\to [5,6,6]\to [1,1,4,4,5,6,6]\to [1,1,4,4,5]$
2,4,6,..番目の配列をつくるときは左側最小化をしていますが、この要素数はこれまで加えられている$u_i$の個数になっています。つまりヒープを用意しておいて$p_i$を2個ずつつっこみ、$i$個になるまで最大値を取り除く操作をしているわけです。そして、この操作後の残っている最大値が、$f_i$の最小値を実現する$u_i$の値になっています。
求めるのは$f_i$の最小値なのでそれを考えます。$f_{i-1}$の最小値が$min_{i-1}$で、$u_{i-1}=argmin_{i-1}$のときに実現するとします。複数ある場合は左端の値としておきます。
まず2個ずつ$p_i$を突っ込むときは特に何もしません。この$p_i$に関しての合計はあとで清算します。$min_i:=min_{i-1}$としておきます。傾き$s_i$を0としておきます。
最大値$curmax$を取り除いて次の最大値が$nextmax$になったとき次のことをします。
- $curmax$が新しく突っ込まれた$p_i$ではない場合、$s_i$を1だけ減らします。イメージとしては左側最小化のグラフの変化点に来た感じです。
- 区間$[nextmax,curmax]$が$(-\infty, argmin_{i-1}]$と交わっている領域について、$min_i$の値が遡上します。交わりの長さを$d$とすると、$min_i$は$d*(-s_i)$だけ増えます。
操作が終わって$argmin_i$が確定したので、新しく突っ込まれた$p_i$それぞれについて$|p_i-argmin_i|$を$min_i$に加えて、$min_i$を確定させます。
以上によって$O(n\log n)$で$min_n$を求めることが出来ます。
例についてこの流れに従って行うと
$heap=[5,5], min_1=0, s_1=0$
$heap=[5], min_1=0, s_1=0, argmin_1=5$ (5は新しく突っ込まれた値なので$s_1$は変化しない)
$min_1+=|argmin_1-5| \to min_1=0$
$heap=[5,8,8], min_2=0, s_2=0$
$heap=[5,8], min_2=0, s_2=0, argmin_2=8$ (8は新しく突っ込まれた値なので$s_2$は変化しない)
$min_2+=|argmin_2-8| \to min_2=0$
$heap=[5,6,6,8], min_3=0, s_3=0$
$heap=[5,6,6], min_3=0+(8-6)\cdot (-(-1))=2, s_3=-1$(8は新しく突っ込まれてない値なので$s_3$が1だけ減っている)
$min_3+=|argmin_3-6| \to min_3=2$
$heap=[1,1,4,4,5,6,6], min_5=2, s_5=0$
$heap=[1,1,4,4,5,6], min_5=2+(6-6)\cdot (-(-1))=2, s_5=-1$
$heap=[1,1,4,4,5], min_5=2+(6-5)\cdot (-(-2))=4, s_5=-2, argmin_5=5$
$min_5 += |argmin_5-1| + |argmin_5-4| \to min_5 = 9$
よって答えは$min_5 = 9$になります。
(余力があったらコードをのっけます)
類題
この問題の類題は自分の知っている限りだと2題あって
ZOJ 3512 Financial Fraud
[東京大学プログラミングコンテスト2012 L じょうしょうツリー]
(http://utpc2012.contest.atcoder.jp/tasks/utpc2012_12)
が該当します。Financial Fraudは、本問の同じ$t_i$の制約がないだけの問題で、じょうしょうツリーは列が木になって広義単調増加が狭義単調増加になっただけの問題です。どちらもここで解説した方法で解けます。
余談
この問題、当初はmeldable heap(高速でマージ可能なヒープ)を使う数少ない問題だと思っていたんですが、この様子だと必要なさそうですね…じょうしょうツリーに関してはヒープをマージするフェーズがあるので、meldable heapを使うと高速に解けますが、使わなくても"データ構造をマージする一般的なテク"によってオーダーをlog n分重くして解くことができちゃいます。