國破れて 山河在り
城春にして 草木深し
時に感じて 花にも涙を濺ぎ
別れを恨んで 鳥にも心を驚かす
峰火 三月に連なり
家書 萬金に抵る
白頭掻いて 更に短かし
渾べて簪に 勝えざらんと欲す
こんにちわ. ブミブミ. 私わ東京大学理学部物理学科のJohn. Tでわありません. Los Angels Dodgers#17 大谷翔平でもないです. 学部満期退学をしたエセ科学者をご存知ですか? 20231219は変化球がなぜ曲がるのか, 審議していきますよ.
基礎方程式とベルヌーイの定理
ここでわ, 簡単のため空気は非圧縮で粘性のない理想流体とみなす. 空気の密度$\rho$, 速度ベクトル$\vec{u}=(u, v, w)$, 圧力$p$対して理想流体の基礎方程式
\frac{\partial \rho}{\partial t}+\nabla\cdot(\rho\vec{u})=0
\frac{\partial \vec{u}}{\partial t}+(\vec{u}\cdot\nabla)\vec{u}=-\frac{\nabla p}{\rho}
が成り立つ. 一つ目の式は粒子数の保存
, 2つ目の式は運動量の保存(運動方程式)である. ここでは, 開いた流体の一部しか考えないのでエネルギーの保存則は使わない. ここでベクトル解析の公式より渦度ベクトル$\nabla\times\vec{u}=\vec{w}$として
(\vec{u}\cdot\nabla)\vec{u}=\nabla(\frac{u^2}{2})-\vec{u}\times\vec{w}
が成り立つので, 定常な流れ$\frac{\partial \vec{u}}{\partial t}=0$の場合, 流線$\vec{u}$に沿って($\vec{u}\cdot\vec{u}\times\vec{w}=0$より)
\frac{p}{\rho}+\frac{u^2}{2}=const.
と表せる. これわベルヌーイの定理と呼ばれる.
流れ関数と速度ポテンシャル
簡単のため2次元で考えることにする. 今$\rho=const.$としているので, 基礎方程式から, $\nabla\cdot\vec{u}=0$がわかる.
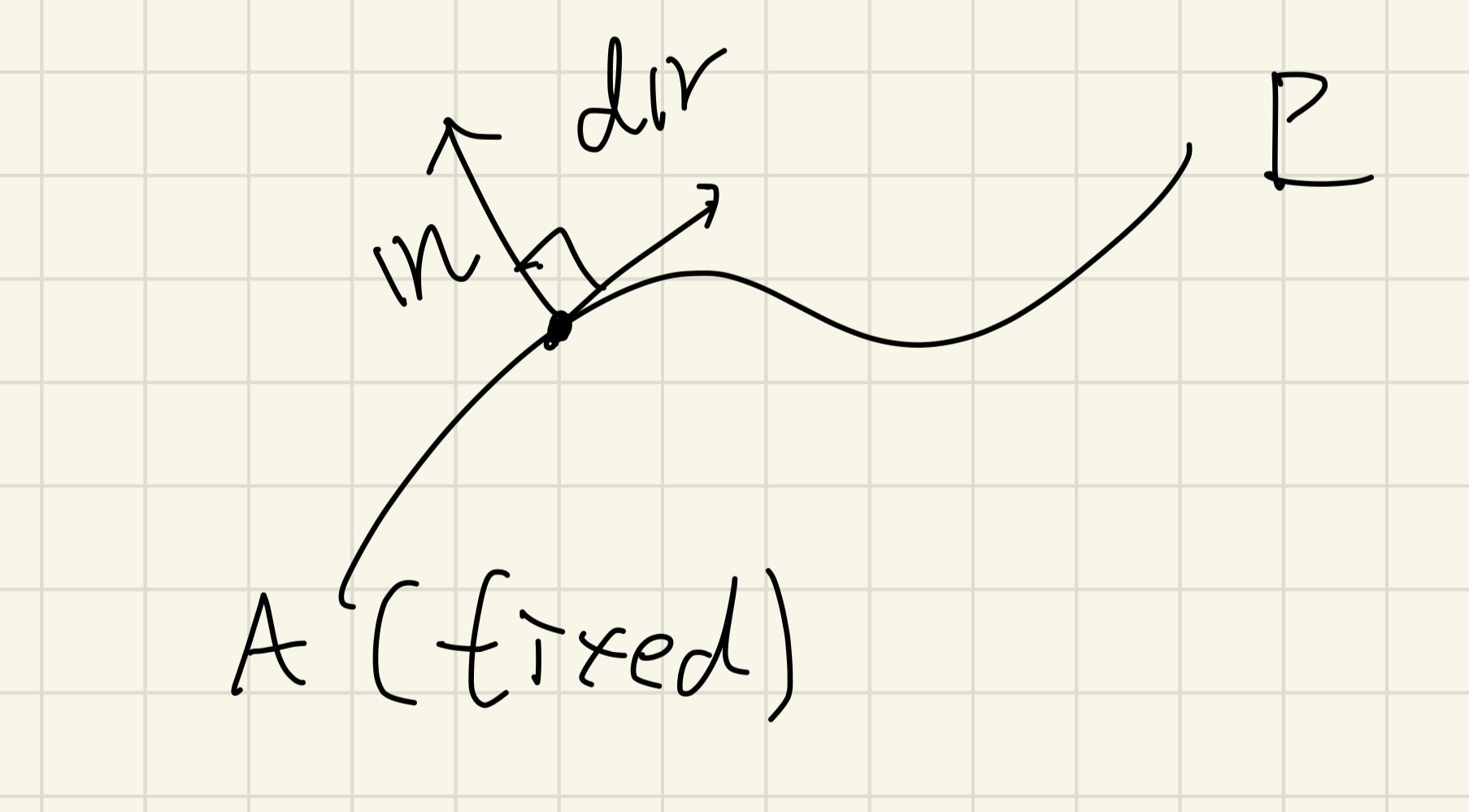
この時, 任意の2点AとPを結ぶ曲線について, 接線$\vec{dr}$に垂直な方向の単位ベクトルを, $\vec{n}$として次の量を考える. ただし, $\vec{n}$は$\vec{dr}$から左に90度回転したものとする.
\Psi=\int_{A\rightarrow P}\vec{u}\cdot\vec{n}dr
この量は$A\rightarrow P$を横切る流れの総量を表し, その経路によらず, 流れ関数と呼ばれる.
流れ関数は次を満たす.
\frac{\partial \Psi}{\partial y}=u, -\frac{\partial \Psi}{\partial x}=v
流線であることと, $\Psi=const.$は等価である.
渦がない場合, (会っても良いが多価関数になるだけ)速度場$\vec{u}$に対してスカラーのポテンシャルを定義できる. それは速度ポテンシャル$\Phi$と呼ばれ, 次を満たす.
u=\frac{\partial \Phi}{\partial x}, v=\frac{\partial \Phi}{\partial y}
この二つはCaushy-Riemannの関係式を満たしている.
\begin{align}
u&=\frac{\partial \Phi}{\partial x}=\frac{\partial \Psi}{\partial y} \\
v&=\frac{\partial \Phi}{\partial y}=-\frac{\partial \Psi}{\partial x}
\end{align}
従って$\Phi$を実部, $\Psi$を虚部に持つ正則関数$f$を定義できる. この正則関数は複素速度ポテンシャルと呼ばれる.
f=\Phi+i\Psi
として定義できる. このポテンシャルで表せる流れをポテンシャル流れという.
複素速度ポテンシャルの例
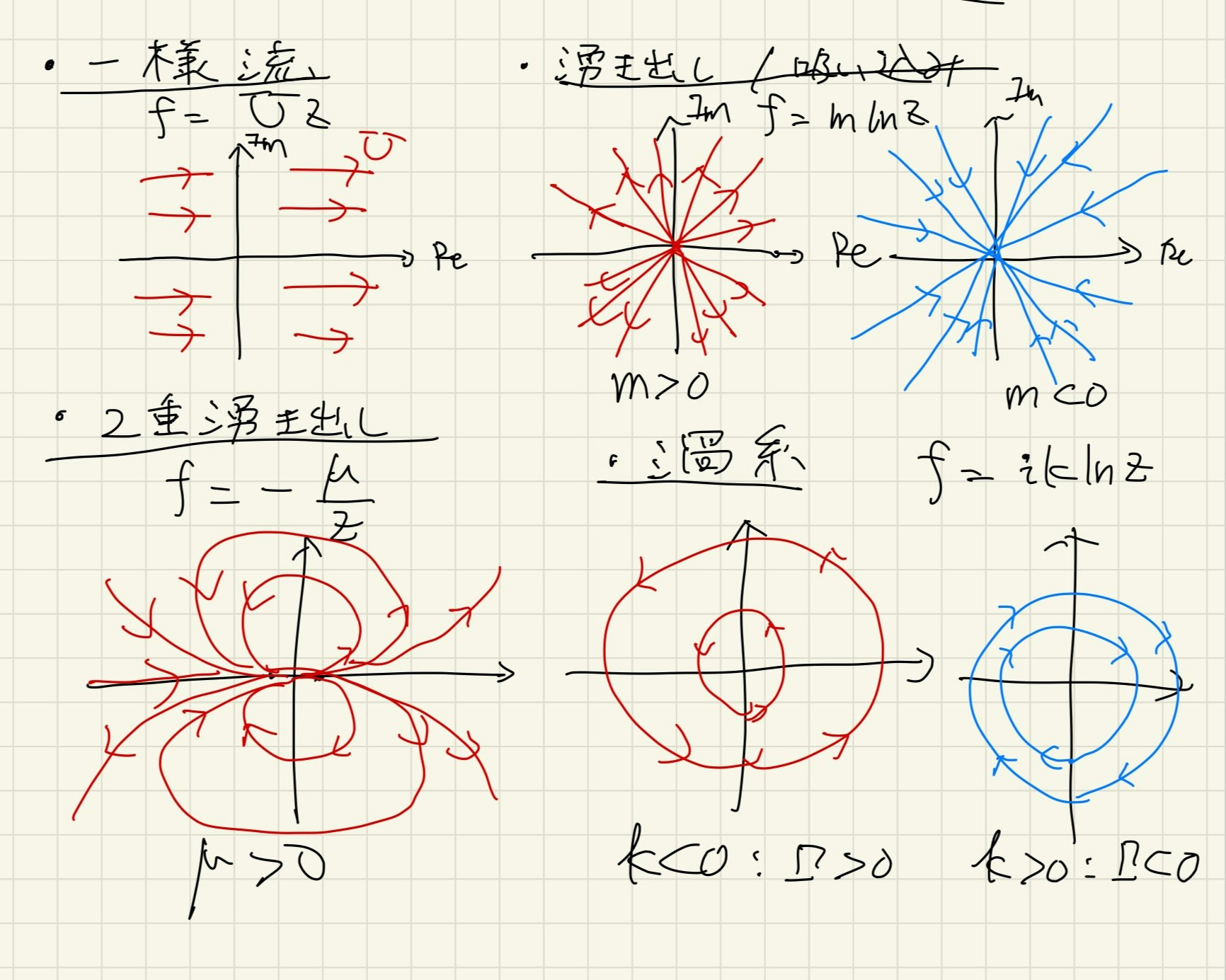
・一様流 $f=Uz$
・原点からの湧き出し $f=m\ln z$
・原点からの二重湧き出し(ダブレット)$f=-\frac{\mu}{z}$
・渦糸$f=ik\ln z$ $k$は渦の強さに対応している $k>0$が右回り, $k<0$が左回りである.
極座標表示すると,
f=ik\ln(re^{i\theta})=ik\ln r-k\theta
半径方向速度$u_r$と接線方向速度$u_\theta$はそれぞれ
u_r=\frac{1}{r}\frac{\partial k\ln r}{\partial \theta}=0,
u_\theta=-\frac{\partial k\ln r}{\partial r}=-\frac{k}{r}
となるので, 半径$r$の円周に沿った速度の積分は
\oint u_\theta\cdot 2\pi rd\theta=-2\pi k\equiv\Gamma
と表せるので, 渦の強さを$k$が表しているとも言える. $\Gamma>0$は, こちらの方が便利なので$k$の代わりにこちらを使うことにする. $\Gamma>0$が左回り, $\Gamma<0$が右回りである.
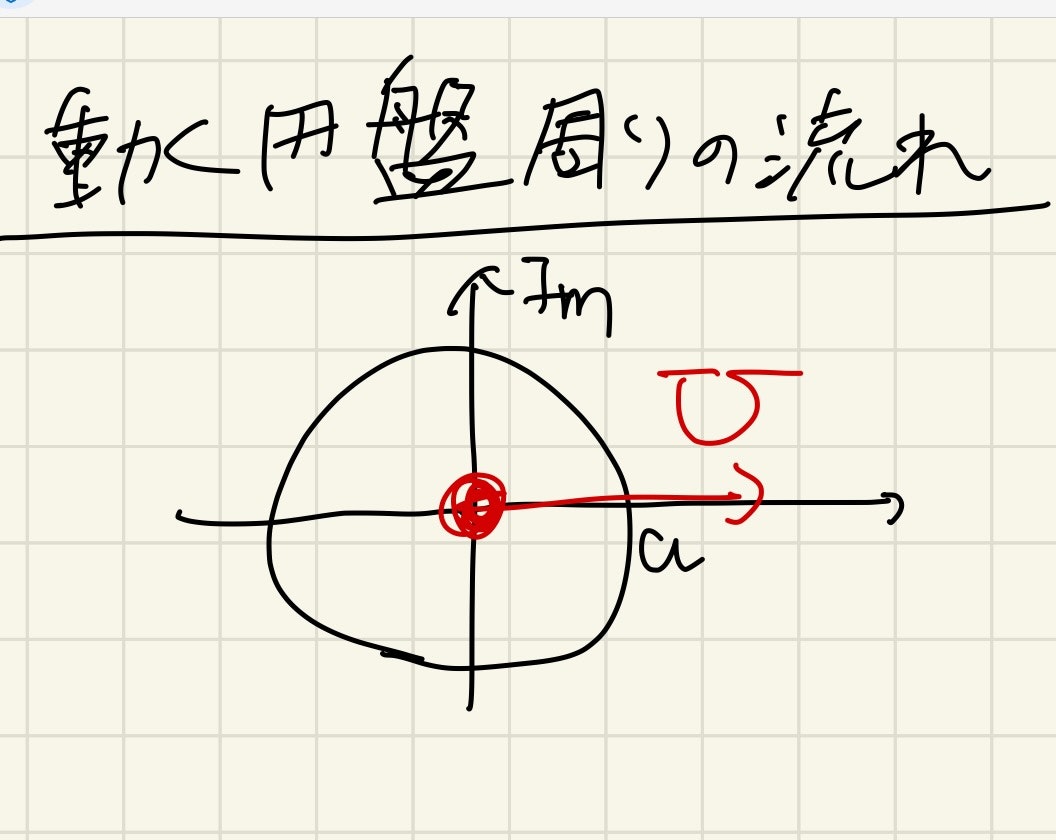
動く円盤周りの流れ
半径$a$の十分薄い円盤が$x$方向に速さ$U$で動いている時のポテンシャルを求めよう.
極座標を用いると, 境界条件として, 円盤表面上では
u_r(r=a)=\frac{\partial \Phi}{\partial r}=U\cos\theta
とあるので, 適当にローラン展開して考えれば, 複素速度ポテンシャル$f$が$r>a$では
f=-\frac{Ua^2}{z}
となることがわかる. これは実際原点周りの2重湧き出しで$\mu=Ua^2$と置いたものである.
一様流れ中の回転しながら動く円盤
$x$方向の速度$-U$の一様流に, 速度$U$で動く円盤を入れる時の複素速度ポテンシャルは, 一様流のポテンシャルと, 動く円盤のポテンシャルを重ね合わせることで,
f=-Uz-\frac{Ua^2}{z}
のように表せる.
この流れに, 円盤を左向きに回した循環を加えると, そのポテンシャルは
f=-Uz-\frac{Ua^2}{z}-i\frac{\Gamma}{2\pi}\ln z
と表される.
極座標表示すると, $f=\Phi+i\Psi$は実部と虚部は
\Phi=-U\left\{ r+\frac{a^2}{r} \right\}\cos\theta+\frac{\Gamma\theta}{2\pi}
\Psi=-U\left\{ r-\frac{a^2}{r} \right\}\sin\theta-\frac{\Gamma\ln r}{2\pi}
となる.
円盤表面$(r=a)$での接線方向速度$u_\theta$は
u_\theta=\frac{1}{a}\frac{\partial \Phi}{\partial \theta}=2U\sin\theta+\frac{\Gamma}{2\pi a}=2U\left\{\sin\theta+\frac{\Gamma}{4\pi Ua} \right\}
となり, $\theta$に依存している.
また, 流線は$r=a$で$\Psi=const.$となっていることから, 円盤そのものである.
ベルヌーイの定理を流線$r=a$に沿って用いると
p(\theta)+\frac{\rho\left\{ (u_\theta)^2+(u_r)^2\right\}}{2}=const.
$r=a$では$u_r=const.$なので結局
p(\theta)+2U^2\left\{ \sin\theta+\frac{\Gamma}{4\pi Ua}\right\}^2=p_0=const.
ともかける. 従って圧力$p$は$\theta$の関数として
p(\theta)=p_0-\left\{ \sin\theta+\frac{\Gamma}{4\pi Ua} \right\}^2
円盤表面で法線ベクトル$\vec{n}=(\cos\theta, \sin\theta)$をかけて積分すると円盤の受ける単位厚みあたりの力になる.
\vec{F}=-\oint p(\theta)\vec{n}ad\theta
簡単な計算によって自明に次のように示される(check by yourself)
F_x=0
F_y=+\rho U\Gamma
これはクッタ・ジューコフスキーの定理, あるいはマグヌス効果と呼ばれる. 動きながら回転する半径$a$の円盤は, 単位厚みあたりに進行方向$(+x)$と回転軸方向$(+z)$の外積の逆方向に, 大きさ$ \rho U\Gamma$の力を受ける. $\Gamma$は回転数に比例した量である. 回転軸方向と回転数, 速度が変化球の曲がる方向を決める, というわけだ. もし半径$a$の球の場合は, これを積分することで, 単位時間あたりの回転数を$n$とすると, 正味の力$\frac{4\pi a^3}{3}Un\rho$を受けると求められる.
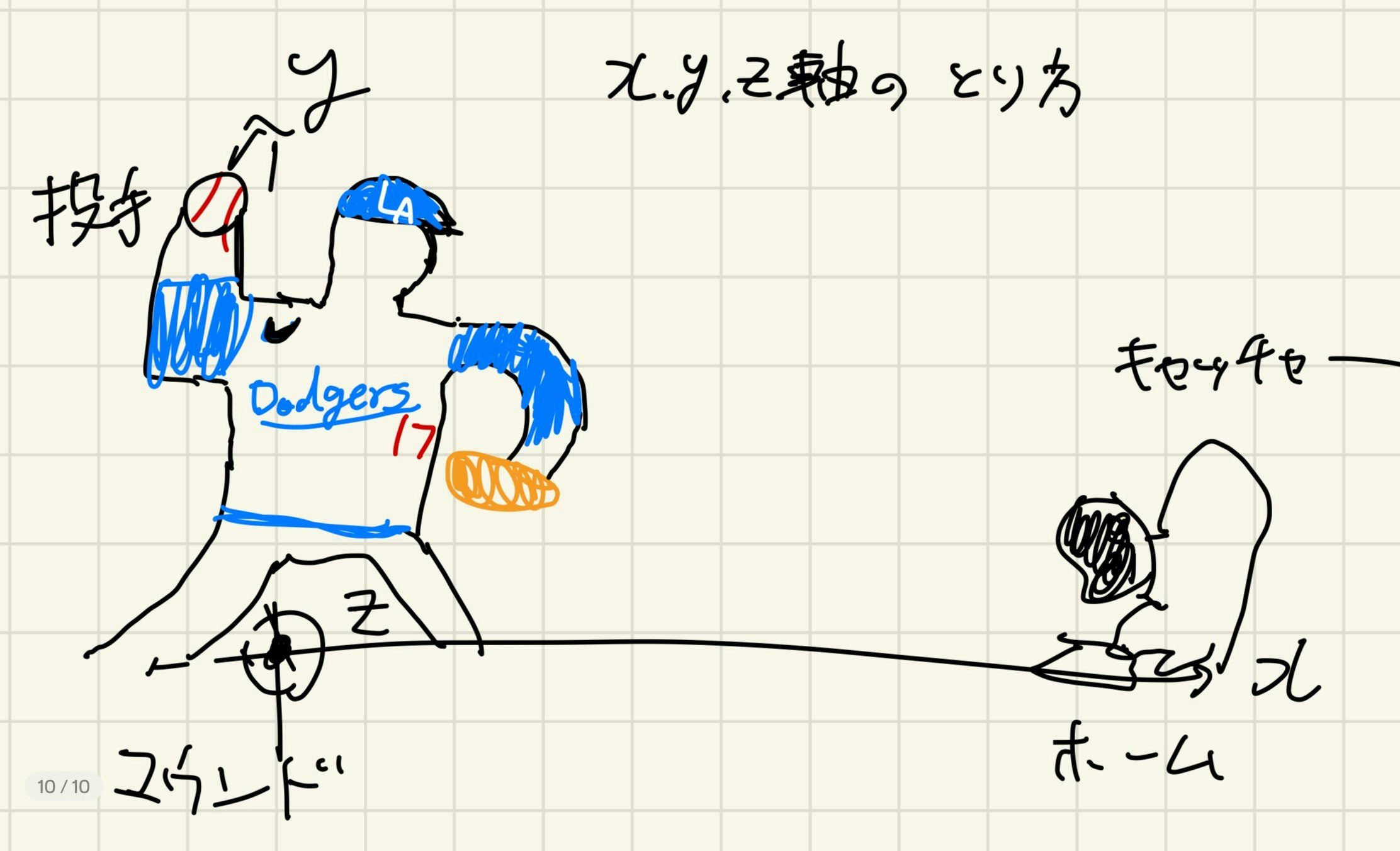
ストレート・フォーク・ナックル
マウンドからホームベースに向かう方向を$+x$方向, 鉛直上向き$+y$方向, マウンドから3塁ベースに向かう方向に$+z$方向にとる.
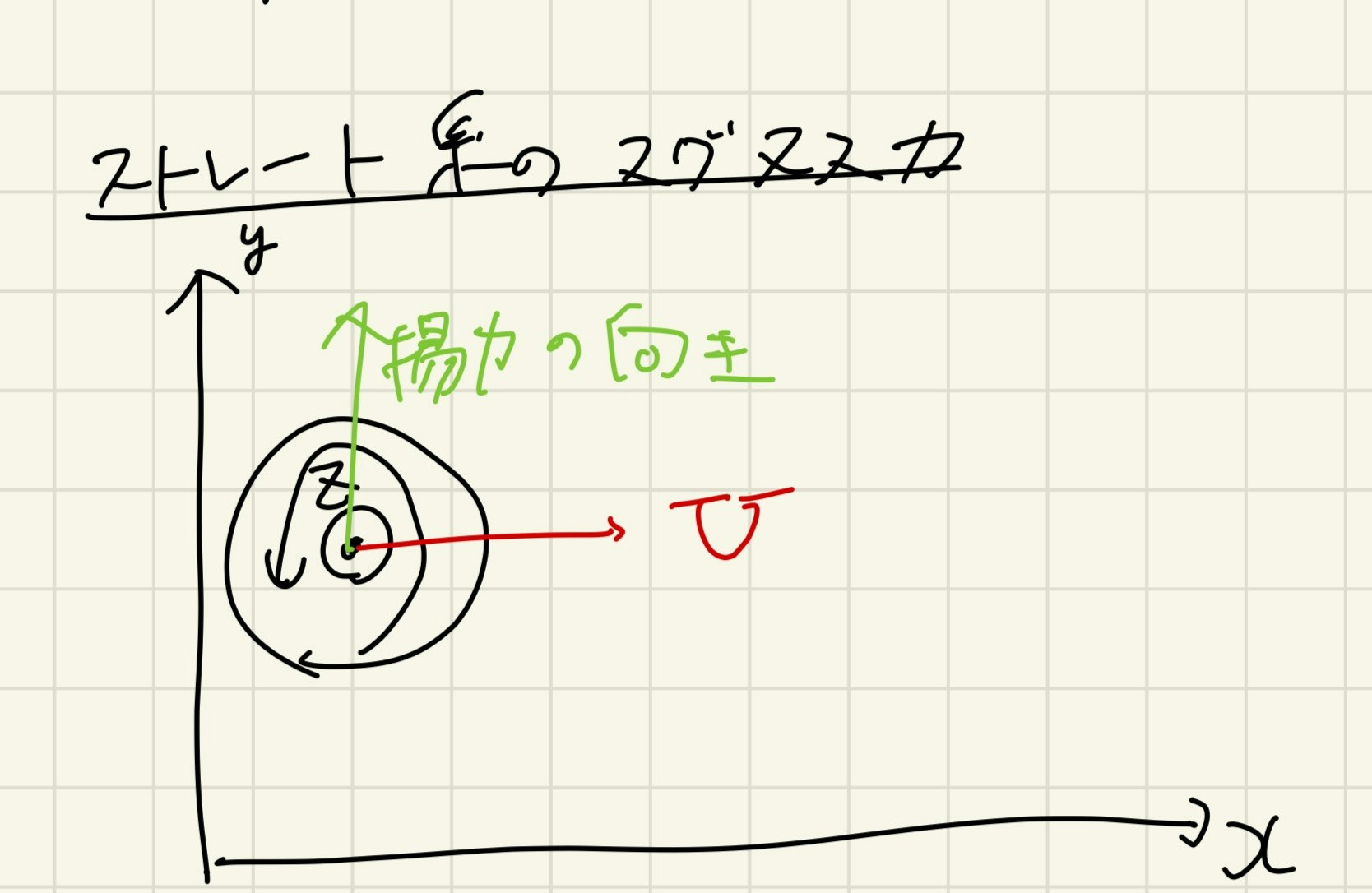
ストレートは進行方向$+x$と回転軸方向$+z$を持つので, 重力だけでなく, 回転数に比例した上向きの揚力が働くことがわかる. これが俗に言うホップするストレートである. フォークやナックルはストレートとほぼ同じだが, 回転数を抑えることで揚力を少なくし, ストレートに比べ, 落とすことができる.
スライダー・カットボール・カーブ
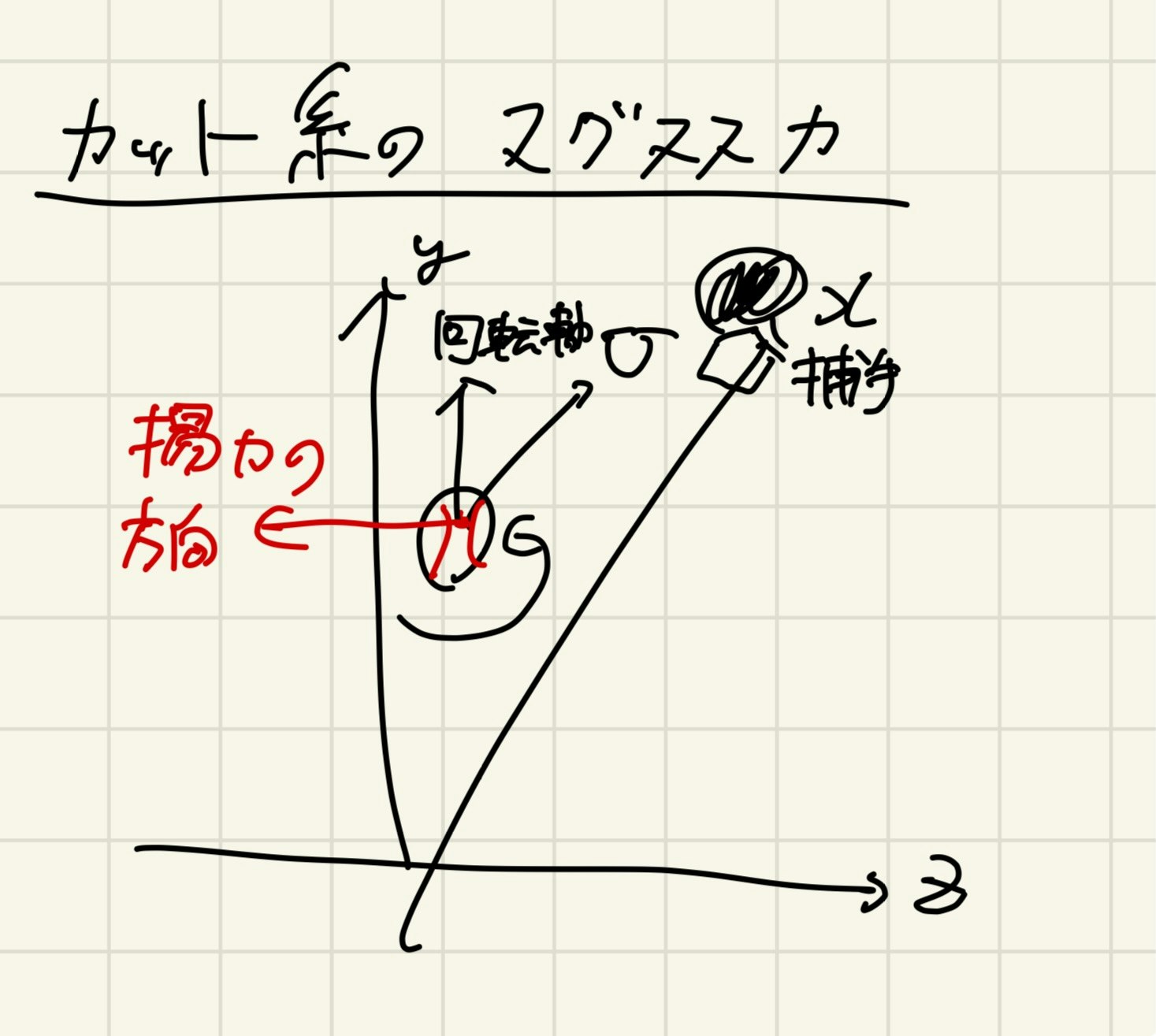
右投手ならスライダー・カットボール系のは回転軸が$+y$方向をむく. つまり, この揚力は$-x$方向, つまり左側に向く. (左投手だと逆になる) つまり利き手と逆側に向かって曲がっていることがわかる. 右投手のカーブの場合は, 回転軸が$+y$方向よりやや$+x$方向の成分も持つため, カット系の球よりも鉛直上むき成分の揚力を持つ. そのため, カーブは一度浮き上がるような軌道に見えるわけだ.
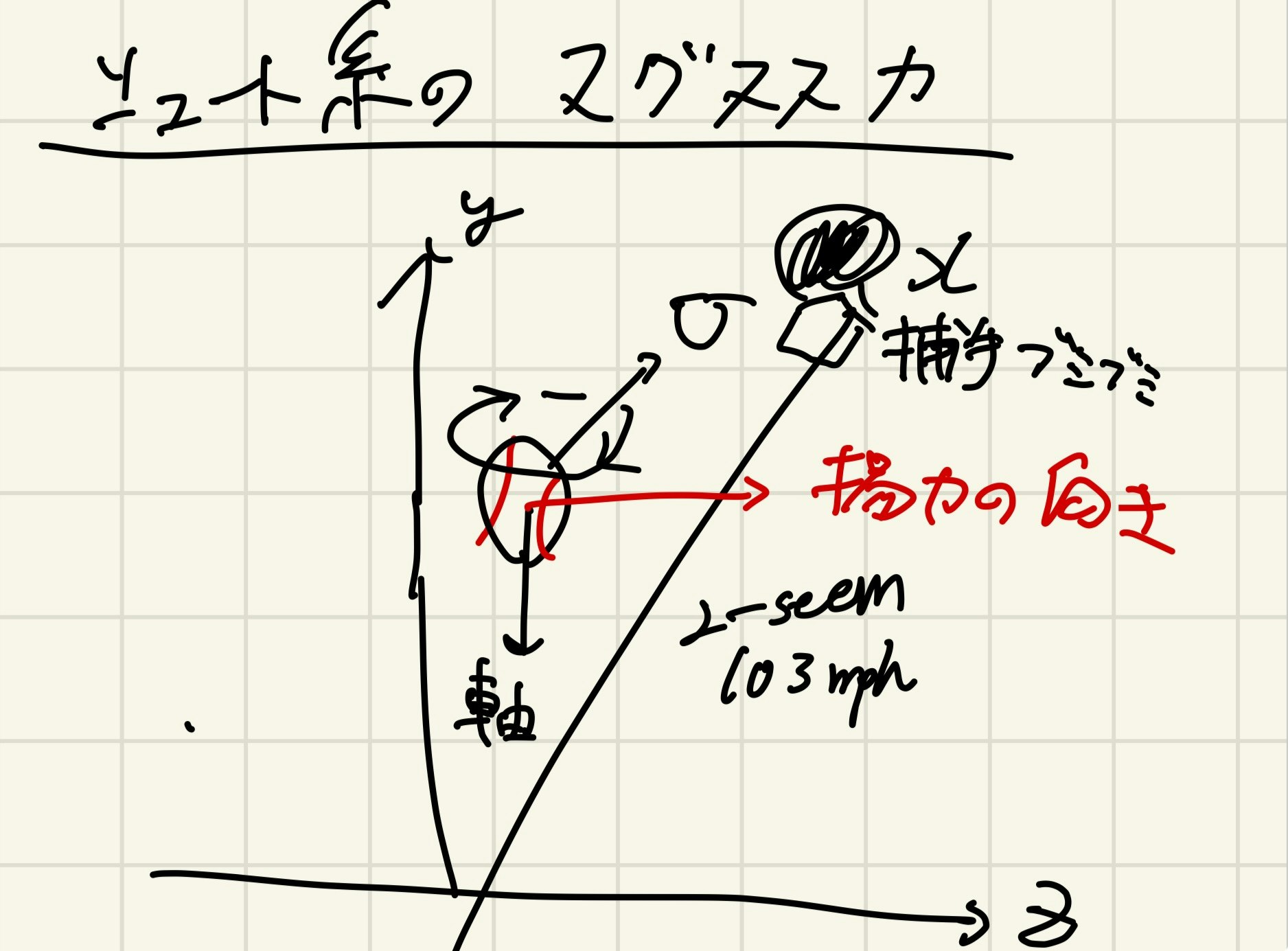
シュート・シンカー・チェンジアップ
カット系と逆向きの回転軸を持つのでカット系の球と逆向きの揚力を受ける. つまり利き手側に変化していく. チェンジアップはシュートやストレートに比べて回転数を落とすので, 受ける揚力の大きさも小さくなるため, シュートに比べて落ちる.
ジャイロボール
回転軸が進行方向に並行な回転はジャイロ回転と言われる. 回転軸が完全に進行方向と一致している場合はこのマグヌス力が働かない. そのため変化量は小さくなる.
球全体の受ける正味の揚力
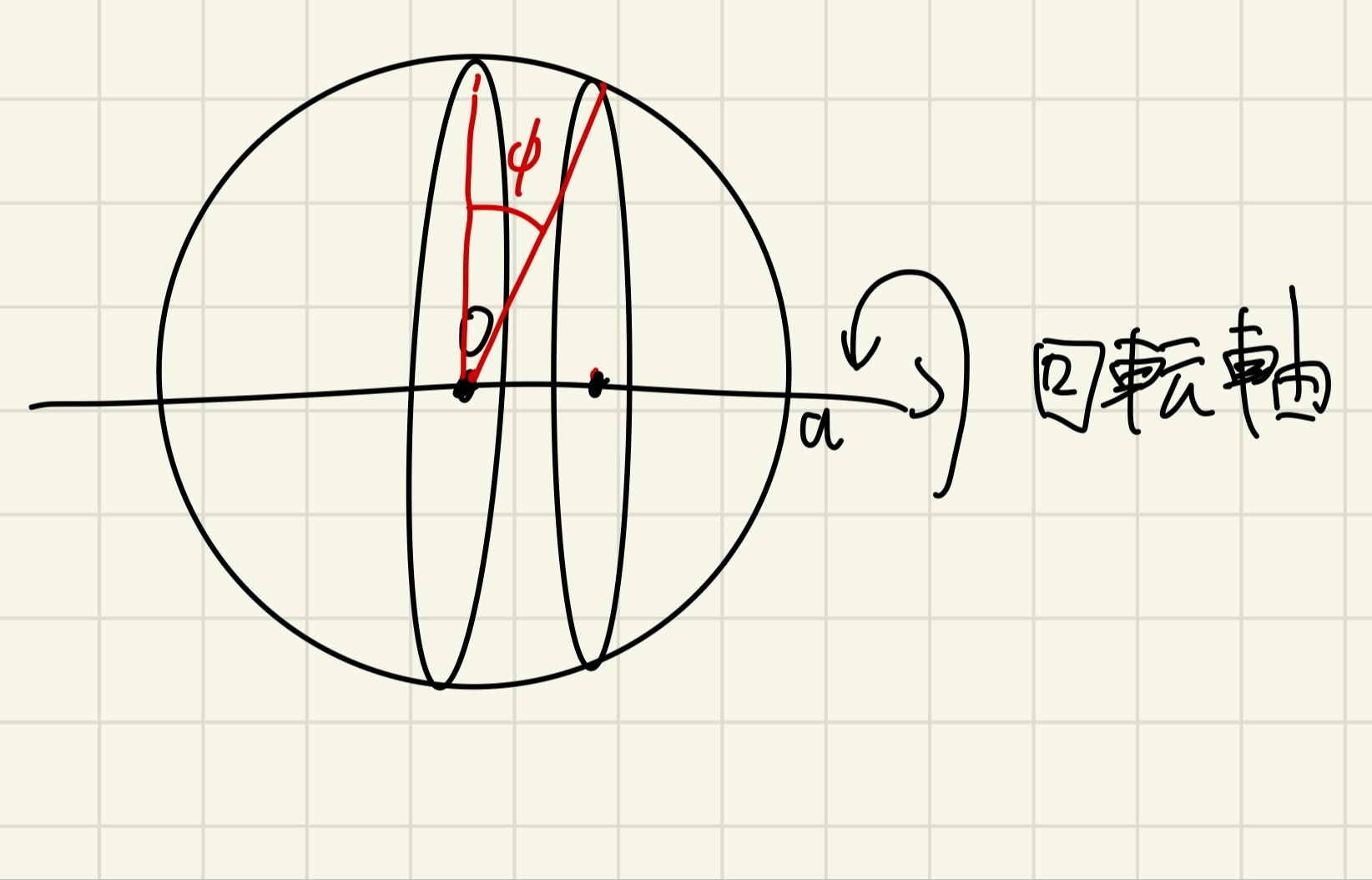
単位時間あたりの回転数を$n$とする. 回転軸に垂直な面で切っているものとして考えよう. 図のように角度$\phi$をとると, 回転数と接線方向速度の関係から次が成り立つ.
u_\theta(\phi)=2\pi n a\cos\phi=\frac{\Gamma}{a\cos\phi}
従って$\Gamma$と回転数$n$の間の関係が
\Gamma=2\pi na^2\cos^2 \phi
とわかる. よって単位厚みあたりの力$\rho U\Gamma$を全ての$\phi$で積分すれば, 球全体にかかる力の大きさ$F_{total}$は
F_{total}=\int_{0}^{\frac{\pi}{2}}\rho U 2\pi na^2\cos^2\phi\cdot a\sin\phi d\phi=\frac{4\pi a^3}{3}Un\rho
終わりに
ここまで長々変化球を流体力学で扱ってきたが, 筆者John T(UT)のできることは, 所詮ボールが投げられたあとの話である. どう投げるかではない. しかしJustin Verlander(HOU)やShohe Ohtani(LAD), Spencer Strider(ATL)のようなどんなに優れた選手・WBC決勝のような緊張した場面でも, 物理学の下にある. そのような場面は彼らのような優れた選手と, 途方もない努力が必要であろうが, 物理学はそこまでではない.(少なくとも身体的な才能や野球の技術は必要ない) みなさんもこの記事をきっかけに物理学に興味を持って, 理学部物理学科に進学すると良いではないか. もちろん, MLBを目指しても良いね.
Reference
Referenceという単語, eが多すぎないか. そんなんだから英語で最も使われるアルファベットがいつまでもeのままなんだ(審議あり)
杉山弘, 遠藤剛, 新井隆景. 流体力学 第2版. 森北出版株式会社, 2014
巽友正, 新物理学シリーズ21 流体力学. 培風館, 1982