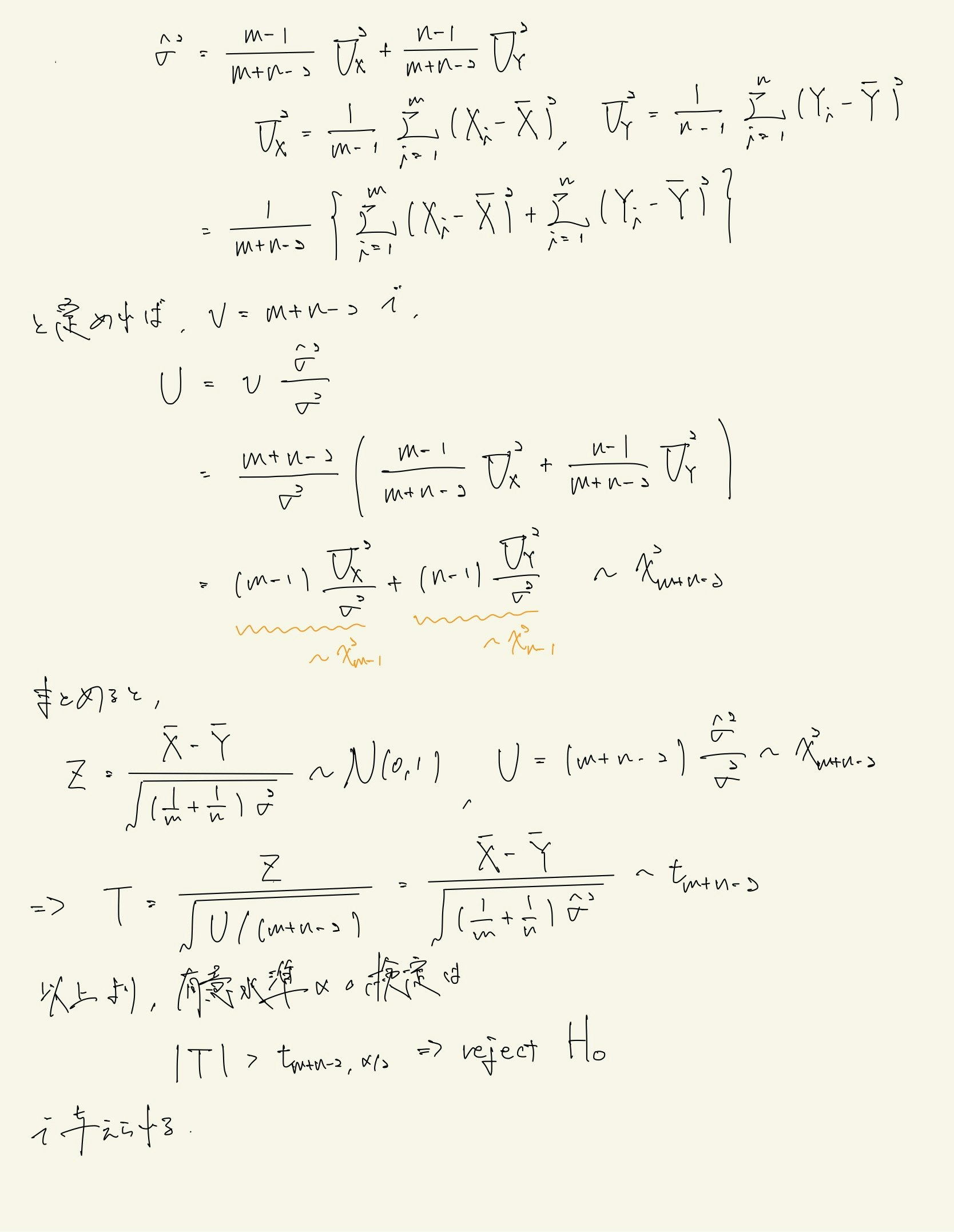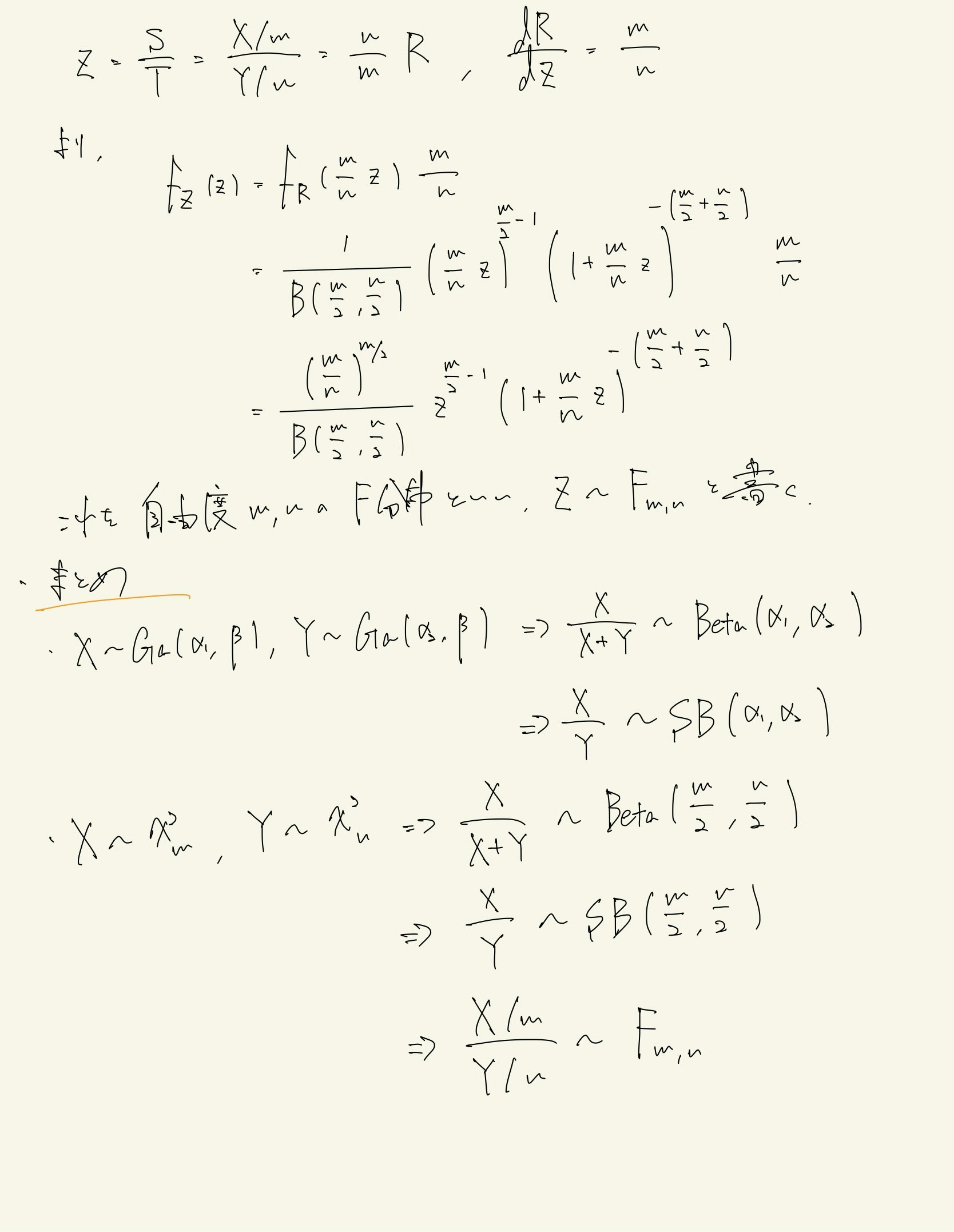方針
メジャーな検定方法を確認しておく.
- 正規分布からの標本
- 平均muの検定→分散既知 or 分散未知
- 平均muの差の検定→分散既知 or 分散未知 (いずれも等分散を仮定)
- 分散sigma^2の差の検定→二標本F検定
- 一般の分布からの標本
- 標本平均の漸近正規性の利用
- 尤度比検定
- 最尤推定量の漸近正規性の利用→ワルド検定,スコア検定
正規母集団の平均muの検定 (分散既知)
正規母集団の平均muの検定 (分散未知)
sigmaが未知である時,sigmaの一致推定量である不偏分散Vを利用する.Vで割るとt分布になる理由は5.2で解説した.
正規母集団の平均muの差の検定 (等分散を仮定)
分散未知の場合は,sigmaの推定量を5.2で確認した事実を利用して導出する.
正規母集団の分散sigma^2の差の検定
正規母集団の平均muの差の検定では,等分散を仮定した.この検定をする前に,二つの母集団の分散が等しいかどうかを検定する.そのために,まずはF分布を導出する.F分布は5.4で扱った.F分布は「カイ二乗分布に従う二つの変数の比が従う分布」である.なおF分布は第二種ベータ分布という「ガンマ分布に従う二つの変数の比が従う分布」の応用版なのでそこから導出する.4.14で二つのガンマ分布の変数変換からベータ分布を導出したことも使う.
検定の話に戻る.二つの正規母集団からそれぞれ標本分散が得られたとすると,帰無仮説のもとでその比はF 分布に従う.
標本平均の漸近正規性の利用
検定統計量が標本平均の形である場合,CLTによって,正規母集団に関する検定を適用できる場合がある.分散既知かどうかは帰無仮説による.
尤度比検定
尤度比検定は,一般の母集団分布からの標本に対して実施できる検定である.
特殊ケースから考えればわかりやすい.帰無仮説のもとでの尤度と,最尤推定したパラメータのもとでの尤度の比を検定統計量とする.次に,この特殊ケースにおいて,棄却のための定数cをどのように決めるのかについて説明する.実は,CRTSは分布収束する.
確率有界とかは正直なんとなくしか分かってない.覚えにくい形ではあるが,テイラー展開の二次の項であることを抑えておけば良い.
最尤推定量の漸近正規性を利用した検定
6.14で確認した事実を利用する.スコア検定では分散を帰無仮説のもとで既知とし,ワルド検定では分散の一致推定量を使う.
本問について
以上で大体の検定は網羅した.本問では,上記のうち尤度比検定,ワルド検定,スコア検定を求める.
答案
参考文献
- 『現代数理統計学の基礎』(久保川達也 著)