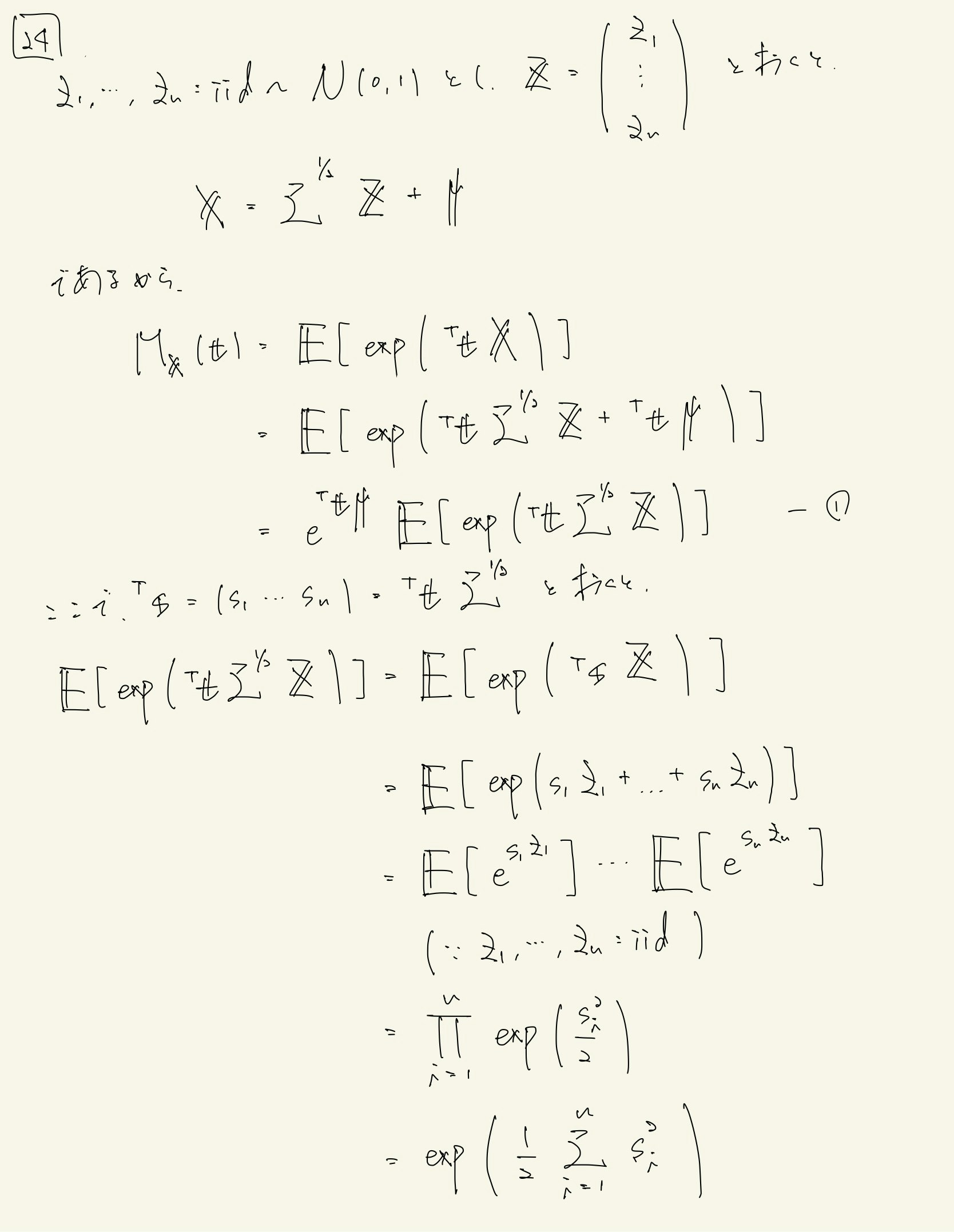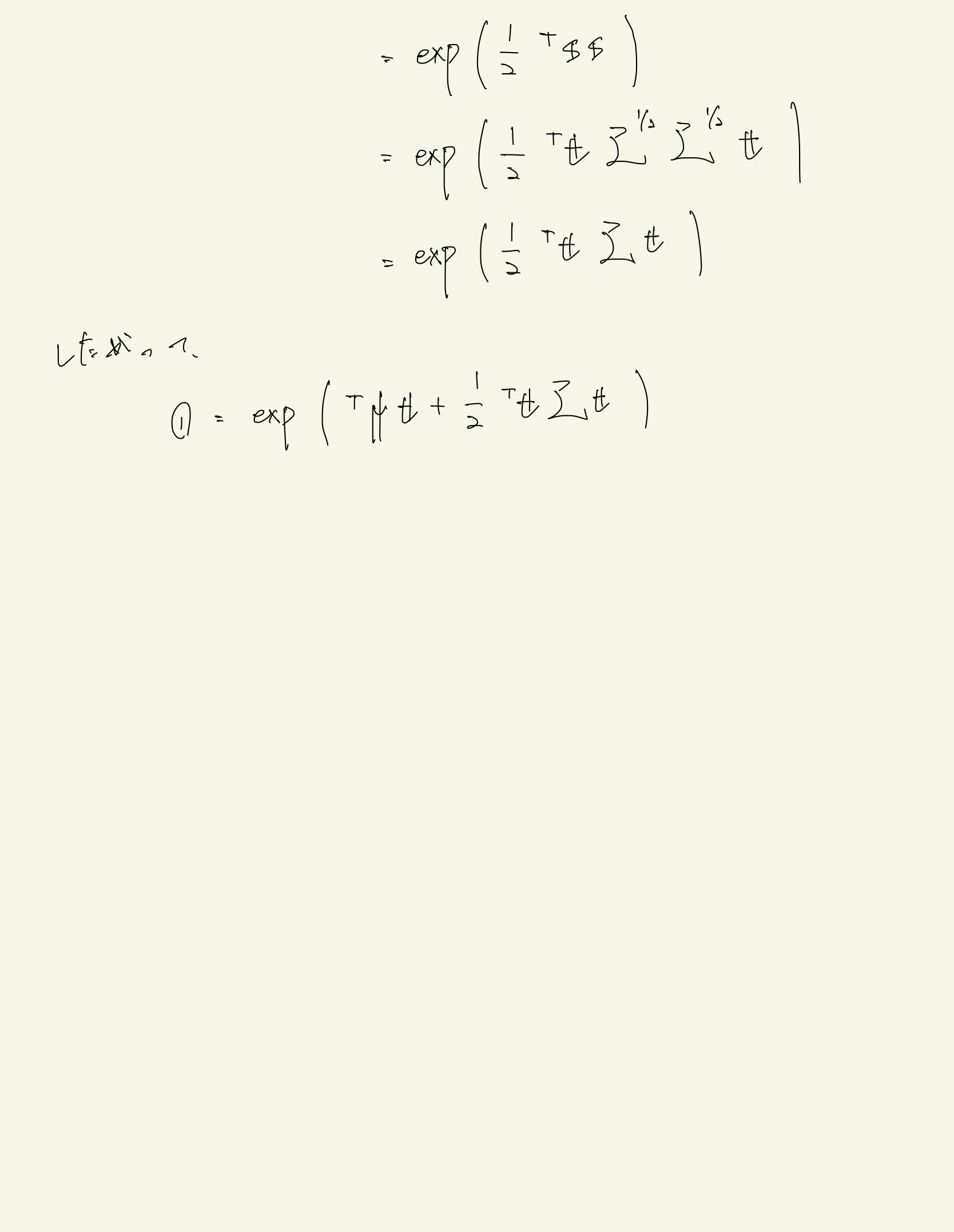方針
Xをそのまま
\begin{align}
\mathbb{E}[\exp({}^\top {\bf tX}]&= \mathbb{E}[\exp(t_1X_1+…t_nX_n)]\\
&= \mathbb{E}[e^{t_1X_1}…e^{t_nX_n}]
\end{align}
と計算しようとすると,ここで手詰まりになる (X_1,...,X_nが独立でないため積の期待値を期待値の積に変形できない) .そこで,独立な確率変数Z_1,...,Z_nを用意してこれの変数変換という形でXを捉えてあげると上手くいく.
答案
参考文献
- 『現代数理統計学の基礎』(久保川達也 著)