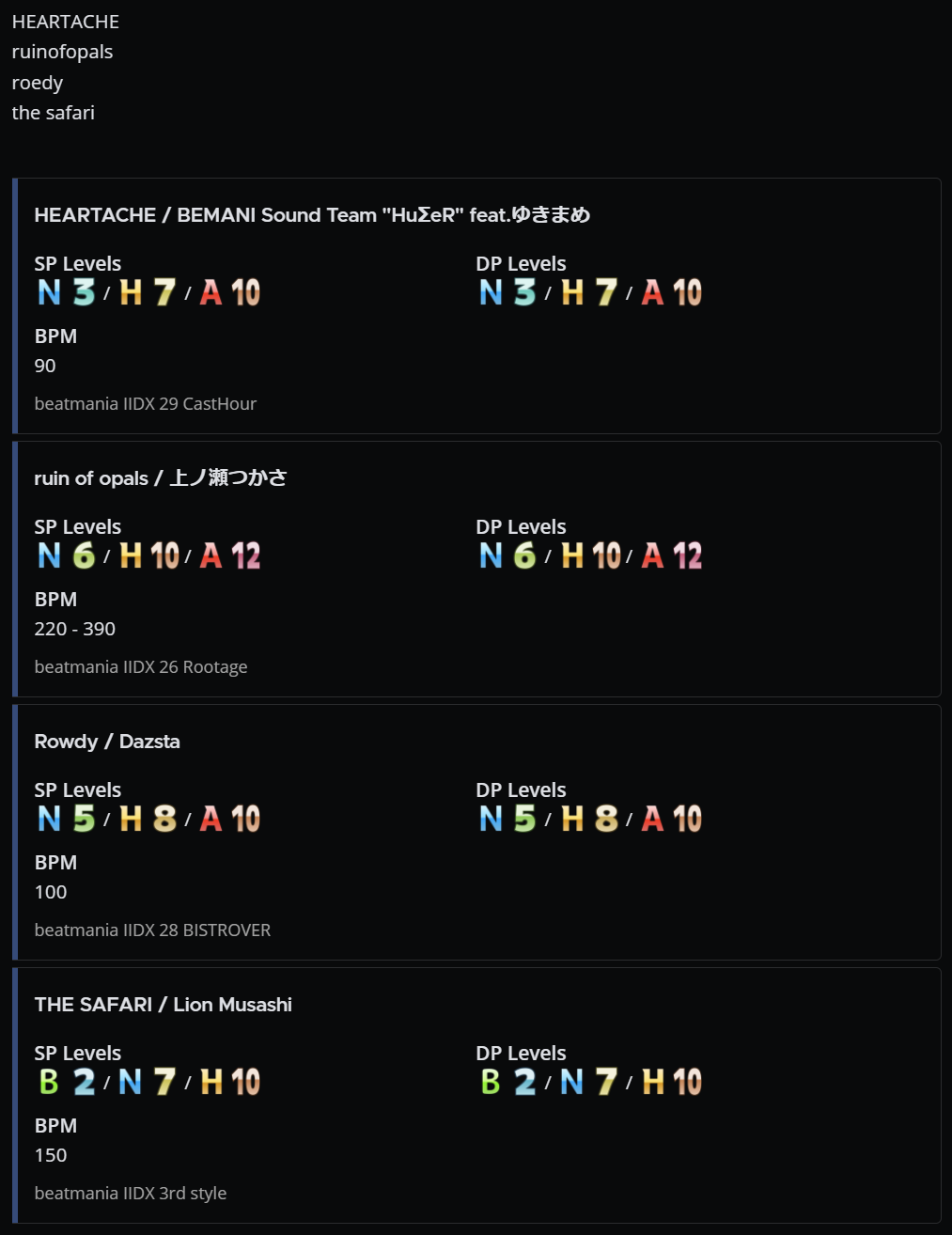
背景
アーケードの音楽ゲームは、そのサービス期間が長くなるにつれて必然的に収録曲数も増えていきます。版権曲を収録しているゲームではライセンスの都合で 2〜3 年で削除されるといったこともありますが、延べ曲数では毎年 50〜100 曲、多いものでは 200 曲近く収録されます。今や合計収録曲数が 1000 曲を超える機種も珍しくなく、例えば 1999 年稼働開始の beatmania IIDX 1 は 2023/12 時点でプレイ可能な楽曲だけで 1700 曲弱も収録されています。
選曲の困難さ
そこで問題になってくるのが「選曲」です。いうまでもなく、楽曲をプレイするためにはまず収録されている曲全体からその楽曲を選択する必要がありますが、ここには大きくわけて次の 2 つのポイントがあると考えられます。
-
検索性 (特定の曲の発見しやすさ)
- 曲名(の一部)や難易度の情報から目的とする曲を発見しやすいかどうか
- 選曲画面でのソート順やフォルダ分けによって変化する
-
操作性 (特定の曲を選択するための操作のしやすさ)
- 選曲画面において、特定の曲にカーソルを合わせるまでの操作が効率的かどうか
- 入力デバイスや UI の構成によって選曲画面でカーソルを移動する速度が異なる
- アーケードの音楽ゲームでは原則として選曲に制限時間があるので、本来プレイしたかった曲に到達する前に時間切れになってしまうことがある
これ以降は主に前者の検索性について取り扱います。
楽曲検索機能
そこで近年導入されつつあるのが楽曲検索機能です。具体的にはソフトウェアキーボードで検索クエリを入力し、検索結果から直接選曲画面のカーソルを移動できるというものです。筆者の知る限り、アーケードの音楽ゲームでは IIDX の LIGHTNING MODEL、 SDVX の Valkyrie Model 2 ぐらいしか実装されている例を知りません。この 2 つはサブモニターとしてタッチパネルを搭載しており、そこにソフトウェアキーボードが表示されて検索ができるようになっています。
この記事の目的は、それらと同じような機能を自前で実装してゲーム筐体以外でも検索できるようにするということです。
検討と考察
実装するにあたっていくつか検討・考察が必要な点があるのでひとつずつ解決していきます。まずは検索クエリの特性や前提についてです。
クエリの「雑さ」を許容するために
Google などでの検索クエリでも同じかもしれませんが、ある程度「雑」に入力したいものです。具体的には、
- アルファベットの大文字・小文字を打ち分けるのは面倒
- スペースを正しい場所に正しい数入力するのは記憶力などの点で難しい
- 記号もキーボードから入力するのが面倒なものがあるので打たなくてもいいようにしたい
- 言葉遊びで別の表記になっている部分については、置換元のまま入力したい
といったところでしょうか。
検索処理でクエリと曲名と比較する際には、これらの特性、あるいは人間的な特徴をうまく組み込んであげる必要があります。
使用するアルゴリズム
次に実際に検索に使用するアルゴリズムを選定しなければなりません。なお、僕があまり詳しくないという理由で今回機械学習による手法は検討していませんが、うまくモデルを構成すれば機械学習でも同じような成果を達成できる可能性は十分ありそうです。
大前提として機械的に正規化することで得られる部分文字列には期待できないので、その時点で部分一致を検索するようなアルゴリズム (Aho-Corasick 法など)は使えません。異なる 2 つの文字列の類似度を判定する方向性でなければならないのです。
この類で代表的なものといえばレーベンシュタイン距離ですね。これは、片方の文字列に対して挿入・削除・置換を最小何回行うことでもう片方の文字列に変換することができるかを計算するもので、計算量も $ \mathrm{O}(mn) $ と比較的優秀です。他にも文字列の類似度を判定するアルゴリズムはいくつかありますが、今回はベースにレーベンシュタイン距離を採用することにしました。実装が比較的シンプルですむのも魅力です。
ただし、素朴な実装では挿入・削除・置換が全て同じコストなので、先ほどの検索クエリの特性とは合致しない点があります。例えば "foo" と "Foos" という曲があるとき、 "foos" という文字列との距離はいずれも 1 になります。しかしクエリとして見た場合、これは "Foos" を全て小文字で打っているだけの可能性が高いため、 "Foos" の方を優先的に、つまりより小さな距離として扱いたいわけです。
アルゴリズムの変更点
そこで、アルゴリズムを改造します。改造といっても、基本的な動作(動的計画法で最小の距離を求める)は変更しません。変更するのは、文字列に対する各操作のコストです。具体的には以下のように変更します。
- クエリの文字から曲名の文字への置換について、
- 小文字→大文字はそれ以外よりも低コストに
- アルファベット→アルファベット以外は高コストに
- クエリ文字列への挿入について、
- スペースの挿入は低コストに
- 記号の挿入も低コストに
- クエリ文字列からの削除について、
- スペースの削除以外は置換・挿入よりも高コストに
- 記号の削除は特に高コストに(クエリに記号を入れているということはかなり意図が強い)
これらを関数やタプルの配列などで表現して、計算式中の距離のインクリメントをそれらへの値に変更しました。
実装 (に関する Rust Tips)
以上の考察をもとに、変更版レーベンシュタイン距離で比較するライブラリを Rust で実装しました。 レーベンシュタイン距離の具体的なアルゴリズムよりは Rust のコーディングテクニックの紹介ですが、実装中に遭遇したいくつかのポイントについて説明していきます。
トレイト境界を構造体側ではなく impl ブロック側で定義する
/// 改造版 Levenshtein 距離を実装するための構造体
pub struct Lyricism<I, D, R, S> {
insert_cost_function: I,
delete_cost_function: D,
replace_cost_function: R,
substring_bonus_function: S,
}
impl<
I: Fn(char) -> usize,
D: Fn(char) -> usize,
R: Fn(char, char) -> usize,
S: Fn(&str, usize) -> isize,
> Lyricism<I, D, R, S>
{
pub fn new(insert: I, delete: D, replace: R, substring: S) -> Lyricism<I, D, R, S> {
Lyricism {
insert_cost_function: insert,
delete_cost_function: delete,
replace_cost_function: replace,
substring_bonus_function: substring,
}
}
}
Rust で構造体にジェネリック型引数を付与する場合、トレイト境界は構造体自体ではなく impl 側に記述したほうが収まりがよくなります。これは、構造体側にどんどんトレイト境界を足してしまうとその構造体をフィールドに含む構造体を記述する際に雪だるま式にトレイト境界が増殖してしまうことによります。 impl 側に書く場合は、 don't care な型引数についてはトレイト境界を書く必要がない他複数のパターンのトレイト境界に対して実装を提供できるので、このパターンの方が好まれる傾向にあるようです。
累積和を scan で求める
let query_distances: Vec<_> = query
.chars()
.scan(0, |sum, c| {
*sum += (self.delete_cost_function)(c);
Some(*sum)
})
.collect();
[1, 2, 3, 4, 5] というリストに対して [1, 3, 6, 10, 15] というような、その要素までの全ての要素の和(累積和)を求める場合、Rust では Iterator::scan メソッドが便利です。おおむね Ruby の scan と同じ機能で、イテレーターの各要素ごと追加の操作を実行できるメソッドです。このとき「追加の操作」から返す値も、また状態の型も元のイテレーターの型と一致している必要はありません。そこで、状態を現在の要素までの和として、各要素ごとに加算して新しいイテレーターの値としてその和を返すことで累積和のイテレーターを容易に得ることができます。
bot 化
最終的にこの検索アルゴリズムを利用して曲名検索 bot を Mattermost 向けに実装しました。ちなみに数曲まとめてクエリを投げても数十 ms で結果が返ってきます。すごい!
おわりに
今回は、音ゲーの曲名を検索するという特定の行為にフォーカスしてレーベンシュタイン距離のアルゴリズムを一部変更してクエリと曲名の距離を計算することで目的を達成しました。ベースのアルゴリズムを大幅に改造しているわけではないので、この変更自体は簡単に行うことができました。
挿入・削除・置換の操作についてはより良いコスト関数を設計することもできそうですし、あるいはレーベンシュタイン距離以外を採用することでひょっとするとより精度の良い検索結果を得られるかもしれません。検索クエリや検索対象文字列の特性を反映する、という点は曲名以外にも応用がききそうです。