Uplift Modelingで介入効果を最適化する

はじめに

広告や医療などの領域において、ある介入をした後の顧客や患者の行動や予後が本当に介入の効果だと言えるのか（純効果がどれほどなのか）を知るのは難しい問題です。しかし、もしそれをうまく予測できれば、事前に介入の純効果がありそうな人となさそうな人を分けた上で効率の良い介入戦略を立てることができます。
この記事では、そのための手法として最近注目され始めているuplift modelingについて紹介します。

目次

• Uplift Modelingとは
• Uplift Modelingの流れ（Two-Model Approach）
• Class Variable Transformationを用いた方法
• 今後について
• 参考

#Uplift Modelingとは
Uplift modelingとは、A/Bテストにより得られたデータを元に介入の純効果を予測することで（広告や医療の分野における）より効果的な介入を目指す手法のことです。
機械学習がuplift modelingと結びつくのは、因果推論における根本問題をどうにかするためです。因果推論における根本問題とは、ある個人について介入された時の結果と介入されなかった時の結果を同時に観測することが不可能であるため、厳密な因果効果を絶対に知ることができないという問題です。
このような問題に対して、観測されなかったどちらかを機械学習の手法を用いてうまく予測することで、これまでA/Bテストでうまくいった戦略を全体に対して適用してきたのを、新たな介入が有効そうな顧客にだけ適用するような細分化をすることで効率的かつ効果的な介入を実現をしよう！というのが基本的な考え方になります。

#UpliftModelingの流れ(Two-Model Approach)
ここではThe MineThatData E-Mail Analytics And Data Mining Challengeのデータセットを用いて、ベーシックなuplift modelingにおける予測手法とされている、Two-Model Approach[1]について簡単にその流れを説明します。
（データセットの詳細はこちらを参照してください。）
今回は「男性向けメール」と「女性向けメール」を誰に送ることでサイト訪問確率を最大化するのかをTwo-Model Approachを使って、考えることとします。

1. 訓練データとテストデータに分ける。

介入実験によって得られたデータのうち、介入群データと統制群データをそれぞれ、訓練データとテストデータに分けます。

# データの読み込み
csv_file = "http://www.minethatdata.com/Kevin_Hillstrom_MineThatData_E-MailAnalytics_DataMiningChallenge_2008.03.20.csv"
df = pd.read_csv(csv_file)

# メールを送らなかった人たちのデータを削除
df = df.loc[df["segment"] != "No E-Mail"].reset_index(drop=True)
df.head()

# カテゴリカル変数をダミー化
categorical_columns = ["zip_code", "channel"]
dummies = pd.get_dummies(df[categorical_columns], drop_first=True)
df = pd.concat([df.drop(categorical_columns, axis=1), dummies], axis=1)

# 説明変数を分けておく
columns = df.drop(["segment","visit","conversion","spend","history_segment"], axis=1).columns
X = df.drop(["segment","visit","conversion","spend","history_segment"], axis=1).values

# 男性向けメールをtreatment, 女性向けメールをcontrolとする
w = np.array(df.segment == "Mens E-Mail").astype(int)
y = np.array(df.visit == 1).astype(int)

# train, test半分ずつに分ける
X_train, X_test, w_train, w_test, y_train, y_test = train_test_split(X, w, y, test_size=0.5, random_state=0)

2. ロジスティック回帰モデルを用いた学習

介入群データと統制群データそれぞれについて、訓練データを用いてサイト訪問ダミー変数
（訪問したら1, 訪問しなければ0）を目的変数として、ロジスティック回帰モデルに学習させます。

# --- Two-Model Approach ---
# 介入群(treat)と統制群(control)それぞれについてロジスティック回帰モデルで学習
lr_treat = LogisticRegression(C=0.1)
lr_treat.fit(X_train[w_train == 1], y_train[w_train == 1])
lr_control = LogisticRegression(C=0.1)
lr_control.fit(X_train[w_train == 0], y_train[w_train == 0])

3. uplift scoreの算出

1で分けておいたテストデータの各サンプルに対し、2で学習した介入群・統制群両方のロジスティック回帰モデルを用いてサイト訪問確率を予測し、uplift score（介入による効果の大きさを表す指標）を算出します。

# (介入を受ける場合のサイト訪問確率) / (介入を受けない場合のサイト訪問確率)をuplift_scoreとして算出
proba_treat, proba_control = lr_treat.predict_proba(X_test)[:, 1], lr_control.predict_proba(X_test)[:, 1]
uplift_score = proba_treat / proba_control

4. 介入戦略の決定

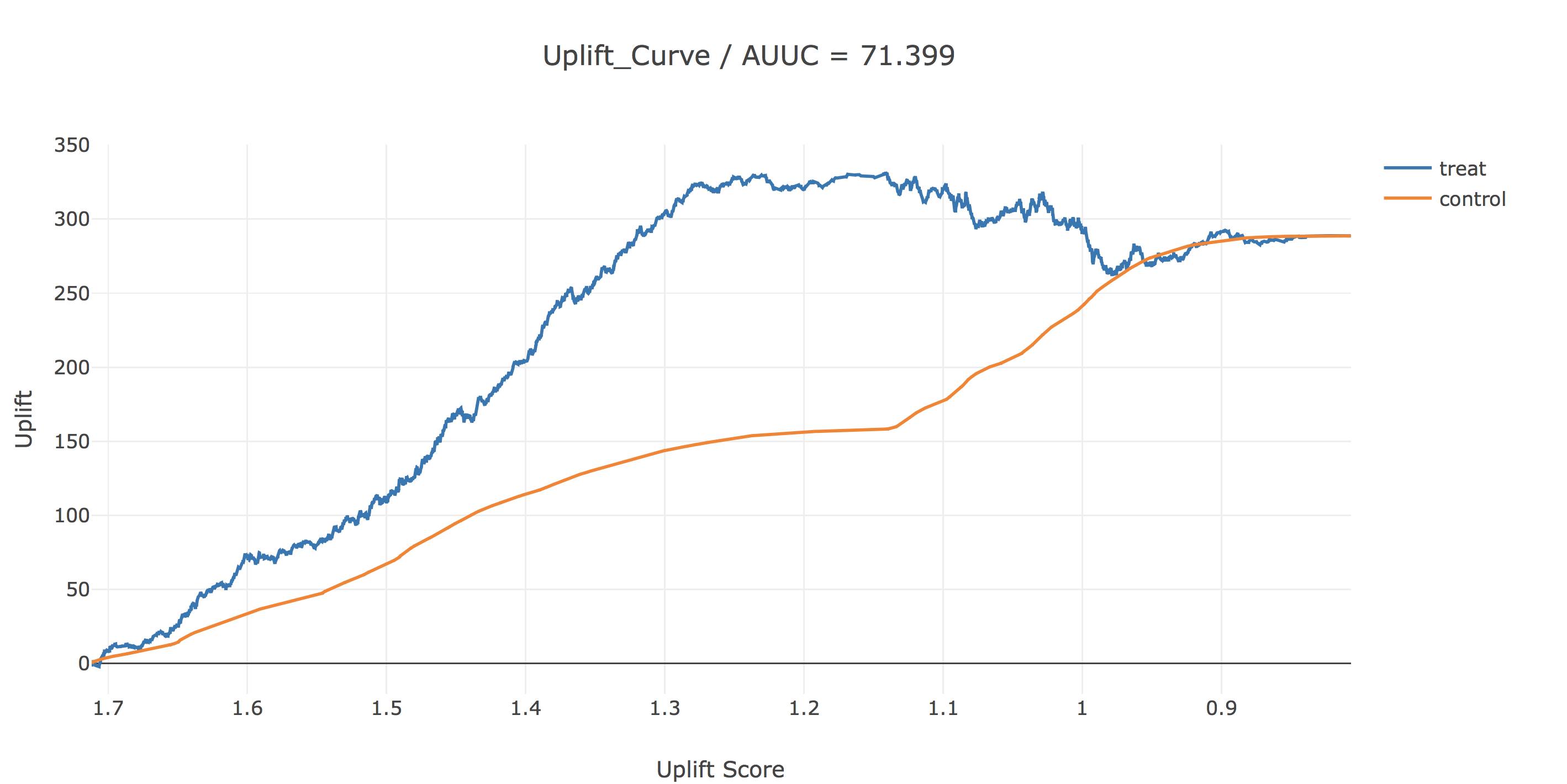
結果を描画することにより、効率的な介入戦略を決定します。今回は、uplift scoreが1.2以上の人に介入するのが良さそうです。ちなみに、AUUCというのは今の所メジャーなupliftの評価指標で、uplift（青線）とbaseline（黄線）の間の面積で計算されます。

uplift（青線）は、横軸で表されるuplift score以上の人のみに介入した時に、全く介入しなかった場合に比べてどれだけサイト訪問が増えるかを表しています。baselineは対象者をuplift scoreとか関係なくランダムに介入した時のサイト訪問数の増分を表してします。

!

#Class Variable Transformationを用いた方法
ここまでのTwo-Model Approachでは、介入群と統制群のそれぞれについて学習器を用いてサイト訪問確率を予測しました。
そして、その比（介入を受ける場合の訪問確率の予測値 / 介入を受けない場合の訪問確率の予測値）をuplift scoreとたところ、uplift scoreが1.2以上の人のみに介入するのが良さそうだという結果になりました。しかし、二つの学習器を用いることによって、パラメータチューニングが難しくなったり、結果の解釈が困難になるという問題点もあります。そこでここからは、一つの学習器のみを用いたuplift modelingの手法であるClass Variable Transformation[2]を先ほどのデータセットに適用した結果を、Two-Model Approachと比較してみます。

###Class Variable Transformationのアイデア
Class Variable Transformationとは、1つの機械学習モデルのみを用いて直接upliftを予測するための手法です。アイデアの根幹を簡単に紹介します。

サンプル集合を$N$とし、任意のサンプル$i\in N$について、特徴量ベクトルを$[X_{i1} ... X_{in}] \in \mathbb{R}$、サイトに訪問したか否かを$Y_i \in \{0,1 \}$、介入を受けたか否かを $G_i \in \{T, C\}$とすると、介入効果 (Treatment Effect)は、$TE_i,=,P^T(Y_i=1,|,X_1 ... X_n), -, P^C(Y_i= 1,|X_1 ... X_n)$ と表せます。
ここで、天下り的ですが、以下のように定義される変数 $Z_i \in \{0,1 \}$ を導入します。

Z_i = \left\{
\begin{array}{ll}
1 & (\, if \, G_i=T \, and \, Y_i=1 \, ) \\
1 & (\, if \, G_i=C \, and \, Y_i=0 \, ) \\
0 & otherwise
\end{array}
\right.

つまり、介入を受けてサイトを訪問した $i$と、介入を受けないでサイトを訪問しなかった $j$について、$Z_i = 1, Z_j=1$となります。
このとき、$Z_i = 1$ となる確率を考えます。

\begin{align}
&P_i(Z_i=1 \, | \, X_{i1}...X_{in}) \\
&= P(Z_i=1 \, | \, X_{i1}...X_{in},G_i=T) \, P(G_i=T \, | \, X_{i1}...X_{in})\\
&+P(Z_i=1 \, | \, X_{i1}...X_{in},G_i=C) \, P(G_i=C \, | \, X_{i1}...X_{in})\\
&=P^T(Y_i=1 \, | \, X_{i1}...X_{in}) \, P(G_i=T \, | \, X_{i1}...X_{in})\\
&+P^C(Y_i=0 \, | \, X_{i1}...X_{in}) \, P(G_i=T \, | \, X_{i1}...X_{in})\\
\end{align}

ここで、ランダム化がうまくいっていると、$[X_{i1} ... X_{in}]$と $G_i$は独立なので、$P(G_i, | , X_{i1}...X_{in}) = P(G_i)$ となります。また、介入群と統制群に割り当てられる確率が等しく、$P(G_i = T) = P(G_i=C) = 1/2 - , (1)$ が成り立っているとします。
このとき、

\begin{align}
&P(Z_i=1 \, | \, X_{i1}...X_{in}) \\
&=P^T(Y_i=1 \, | \, X_{i1}...X_{in}) \, P(G_i=T) \\
&+P^C(Y_i=0 \, | \, X_{i1}...X_{in}) \, P(G_i=C) \\
&=P^T(Y_i=1 \, | \, X_{i1}...X_{in}) \, P(G_i=T) \\
&+(1-P^C(Y_i=1 \, | \, X_{i1}...X_{in}) \, P(G_i=C)) \\
\\
&2P_i(Z_i=1 \, | \, X_{i1}...X_{in}) \\
&=P^T(Y_i=1 \, | \, X_{i1}...X_{in})+(1-P^C(Y_i=1 \, | \, X_{i1}...X_{in})) \quad \because \, (1)
\end{align}

最後の式を変形すると、$P^T(Y_i=1,|,X_{i1} ... X_{in}), -, P^C(Y_i= 1,|X_{i1} ... X_{in})=2P_i(Z_i=1 | X_{i1}...X_{in}) - 1$ となることから、$i$について$Z_i=1$となる確率を予測することで、$TE_i$を予測することになっています。そしてこの方法により、一つの学習器のみで介入効果を予測することが可能となります。

ここから、Two-Model Approachと同じような流れでClass Variable Transformationを用いたuplift modelingを試してみます。

1. 訓練データとテストデータに分ける。

# zラベルを作成
z = w_train * y_train + (1 - w_train) * (1 - y_train)

# P(G=T) = P(G=C) = 1/2 が成り立っているかを簡単に確認
df[df.segment == "Mens E-Mail"].shape[0] / df.shape[0]

#-------------------------------

0.4990631 # 大丈夫そう

#-------------------------------

2. ロジスティック回帰モデルを用いた学習

# Class Variable Transformation
lr_z = LogisticRegression(C=0.1)
lr_z.fit(X_train, z)

3. z-scoreの算出

# z scoreの算出(z score = 2P(Z=1|X) - 1)
z_score = 2 * lr_z.predict_proba(X_test)[:, 1] - 1

4. 介入戦略の決定

ここでは、先ほどよりも詳しく描画してみます。

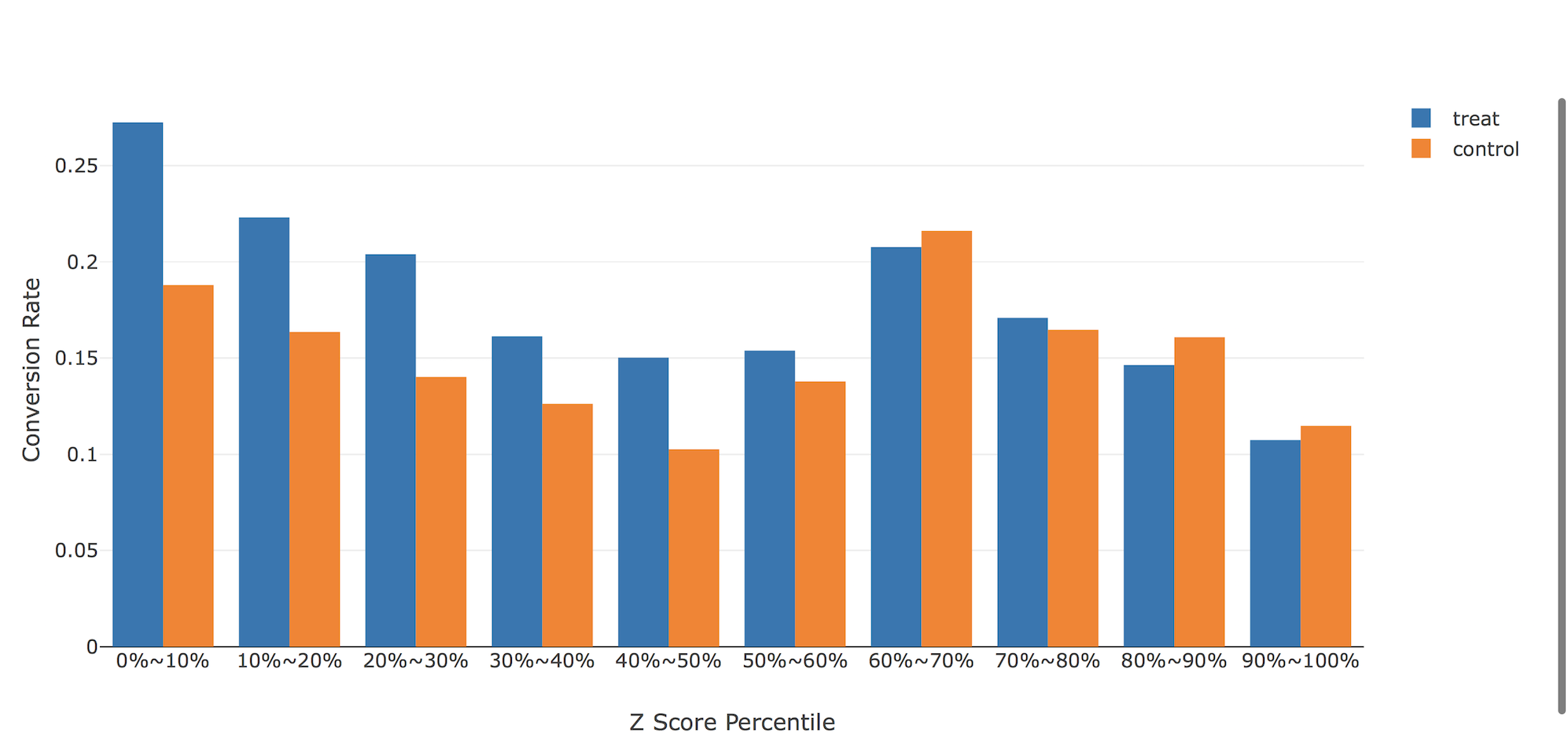
こちらの図は、z scoreが上位（treatment、つまりMens E-Mailが有効と予想される順）のサンプルから並べて全サンプルを10分割したときの、介入群と統制群の実際のサイト訪問率を表しています。z scoreが上位50-60%より上の人たちには、「男性向けメール」それより下位の人たちには（あまり差がありませんが...）「女性向けメール」が有効そうであると言えます。

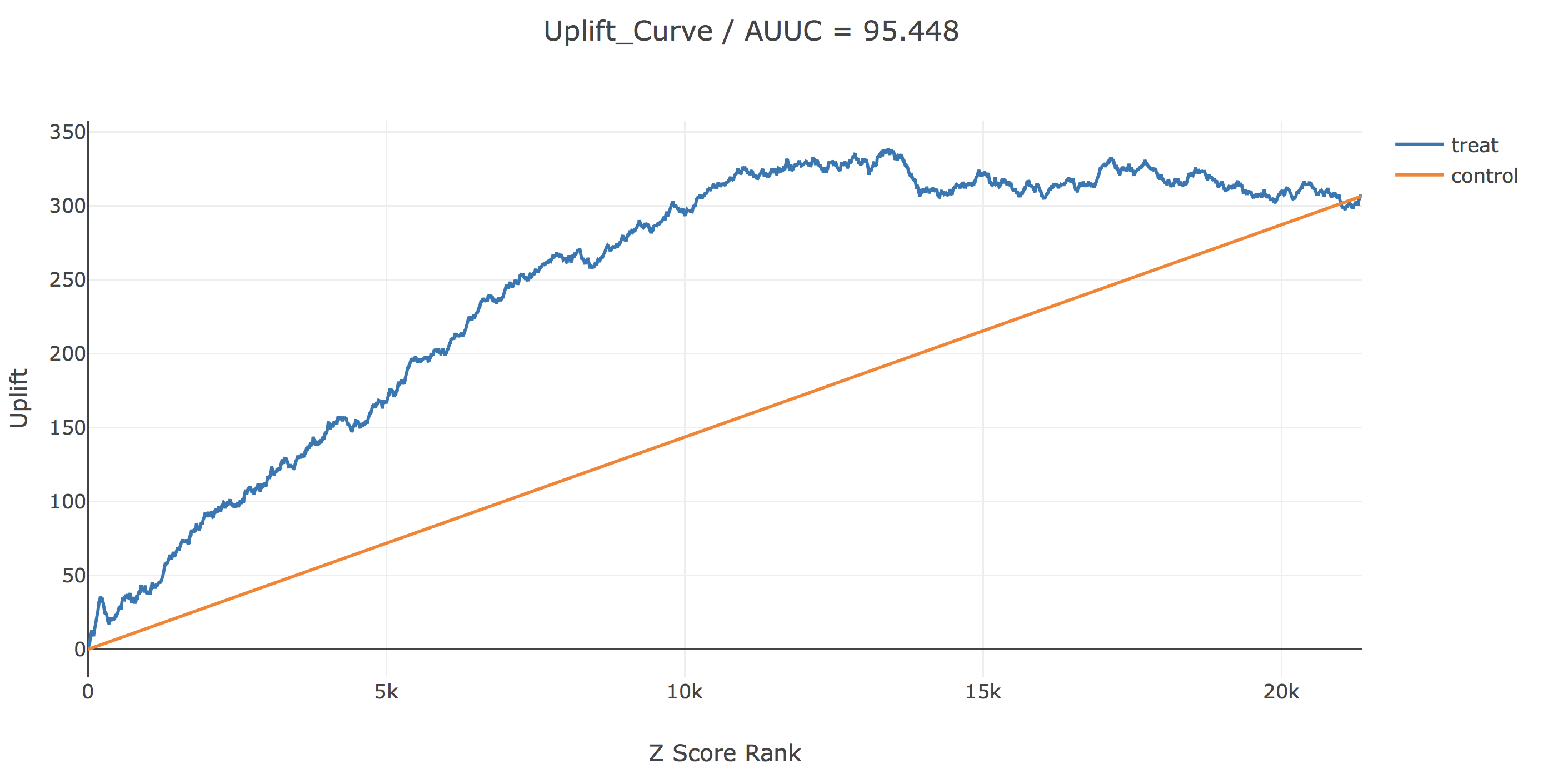
次に、z scoreが大きい人から順に並べたときのupliftのグラフです。今回のデータにはだいたい2万人強の人がいましたが、Z scoreが上位1.3万人くらいの人に「男性向けメール」それより下位の人に「女性向けメール」を送ると最もupliftを稼げそうです。ちなみに、AUUCはTwo-Model Approachに比べて20以上改善しています。

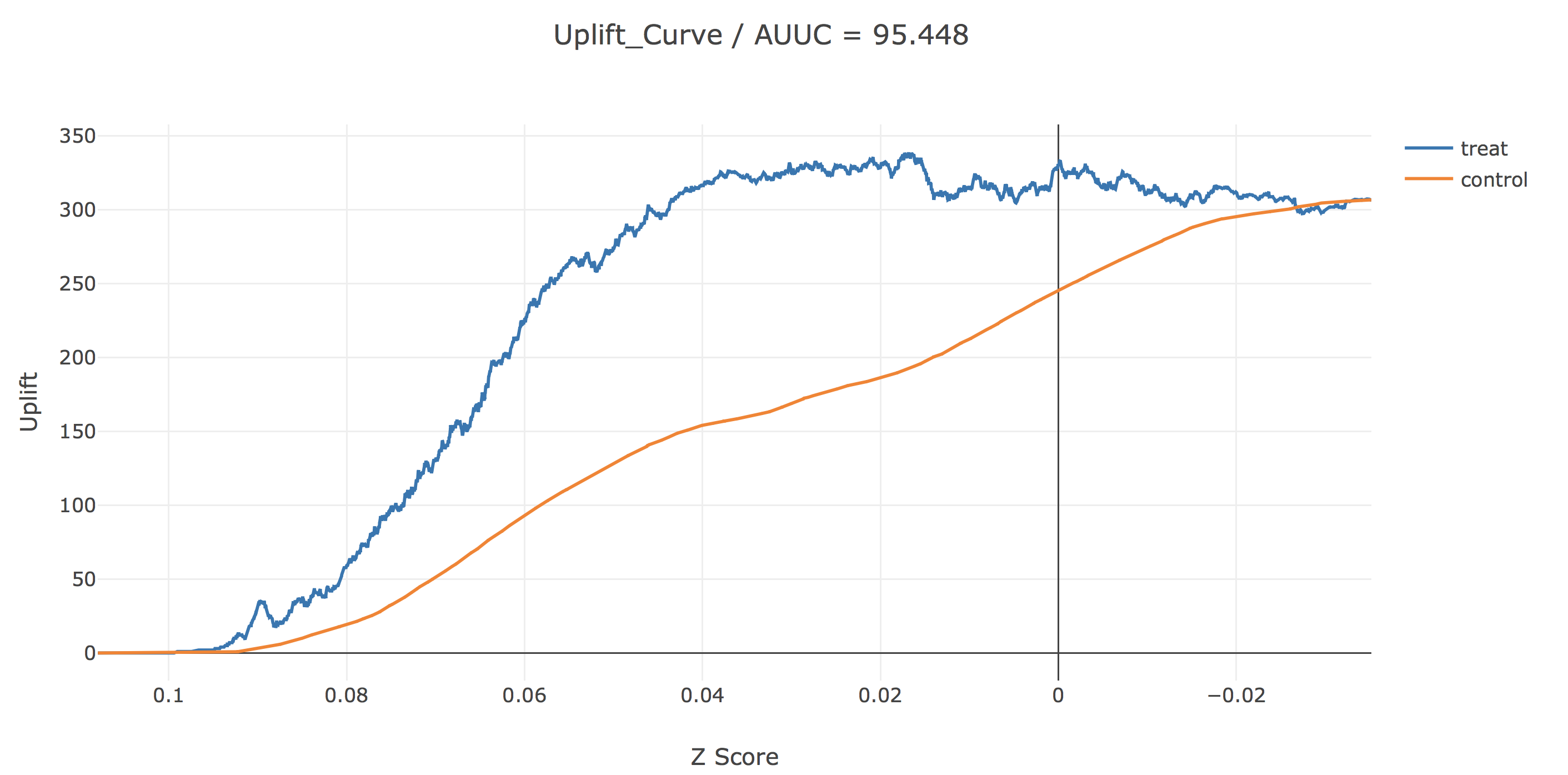
最後に、Two-Model Approachの時も見た横軸にz scoreをとった図ですが、先ほどとはだいぶ様相が変わっているように見えますね。z scoreは介入した場合の訪問確率と介入しなかった場合の訪問確率の差の推定量ですので、結果の解釈がしやすくなっていると思います。（これを一つの学習器で予測するのがこのアプローチの利点でした。）この図からは、z-scoreがおおよそ0.017以上、つまりサイト訪問確率を介入によって1.7%以上改善できると予測された人のみに介入するのがupliftを多く稼げると解釈することができます。

5. 特徴量の重要度を見る

Class Variable Transformationのもう一つの利点として、一つの学習器のみを用いているため純効果に対する各特徴量の重要度を分析することができることが挙げられます。ここでは、簡単に先ほど学習させたロジスティック回帰モデルの回帰係数を見てみます。

# z scoreを算出したロジスティック回帰モデルの係数を表示
for feature, coef in zip(columns, lr_z.coef_[0]):
    print(f"{feature} / {round(coef, 4)}")

# feature / coefficient
---------------------------------------------
recency  /  -0.0057
history  /  0.0
mens  /  0.1186
womens  /  0.0022
newbie  /  -0.0352
zip_code_Surburban  /  -0.0315
zip_code_Urban  /  -0.0064
channel_Phone  /  0.0086
channel_Web  /  0.0045
---------------------------------------------

これを見てみると、元々のデータセットでは男性・女性にかかわらず「男性向けメール」「女性向けメール」を送っていましたが、実は「男性向けメール」はちゃんと過去に男性向け商品を買った人に効果的だったことが読み取れます。
また、Class Variable Transformationでは学習器が1つであるため、ロジスティック回帰以外の機械学習モデルも容易に適用できますが、Random ForestやSupport Vector Machineを用いてみてもAUUCが改善しませんでした。(probability calibration 等は使用していない。)

#今後について
これからは、以下の内容について勉強していきたいです。勉強が進んだら続編を書こうと思います。

• Uplift-Modelingに特化したEnsemble学習
• 多クラス問題（今回削ってしまった"メールを送らない"も含めた分析）や回帰問題におけるUplift-Modeling
• AUUCなどを最適化するためのパラメータチューニング（今回はしっかりとチューニングしていない）

#参考
[1] 有賀康顕, 中山心太, 西林孝. 仕事で始める機械学習, オライリー・ジャパン, 2017
[2] Jaskowski, M and Jaroszewicz, S. Uplift modeling for clinical trial data. In ICML Workshop on Clinical Data Analysis, 2012.