はじめに
前回、『傾向スコアを用いて観察データからUpliftをモデリングする』では、傾向スコアによるバイアス補正により観察データを用いてもUplift Modelingが可能であることをCM視聴による介入のスマホアプリ利用時間に対する因果効果を効率化することで示しました。
前回、スマホアプリの利用時間にアウトカムを絞ったのは、傾向スコアによる補正が分類問題に対して当てはめることが正しいのか否かを推し量りかねていたからなのですが、今回はスマホアプリ利用ダミーをアウトカムとして傾向スコアによる補正を用いたUplift Modelingを実験的にやってみた結果をまとめることとします。
なお、利用データや傾向スコアによるバイアス補正の方法は、前回記事『傾向スコアを用いて観察データからUpliftをモデリングする』を踏襲しています。
*本記事で使用したコードはこちら (adj-uplift-modeling2.ipynb) からご覧いただけます。
傾向スコアを用いたUplift Modelingの分類問題への応用
Class Variable Translation
まずはじめに、Class Variable Translationという1つの機械学習モデルのみを用いて直接Upliftを予測するための手法を試してみます。ここではまだ、傾向スコアによる補正をしていません。
Crass Variable Translationでは、サンプル集合を$N$とし、任意のサンプル$i\in N$について、特徴量ベクトルを$[X_{i1} ... X_{in}] \in \mathbb{R}$、スマホアプリを利用したか否かを$Y_i \in \{0,1 \}$、CM視聴という介入を受けたか否かを $G_i \in \{T, C\}$とした時に、変数 $Z_i \in \{0,1 \}$ を導入します。
Z_i = \left\{
\begin{array}{ll}
1 & (\, if \, G_i=T \, and \, Y_i=1 \, ) \\
1 & (\, if \, G_i=C \, and \, Y_i=0 \, ) \\
0 & otherwise
\end{array}
\right.
すると、個人介入効果 $ITE_i(Individual , Treatment , Effect)$を、$ITE_i,=,P^T(Y_i=1,|,X_1 ... X_n), -, P^C(Y_i= 1,|X_1 ... X_n) = 2P_i(Z_i=1 | X_{i1}...X_{in}) - 1$ により予測できることを利用した手法です。より詳しく知りたい方は、『Uplift-Modelingで介入効果を最適化する』を参照してみてください。早速この方法を用いて、Uplift Modelingを試みます。
# データの読み込み
data_df = pd.read_csv('https://github.com/iwanami-datascience/vol3/raw/master/kato%26hoshino/q_data_x.csv')
data_df.head()
# 説明変数
cols = ["child_dummy", "area_kanto", "area_tokai", "area_keihanshin",
"T", "F1", "F2", "F3", "M1", "M2"]
X = data_df[cols]
# Zラベルの作成
Z_df = data_df[["cm_dummy", "gamedummy"]].drop_duplicates()
Z_df["Z"] = np.array([1, 0, 0, 1])
data_df = pd.merge(data_df, Z_df, on=["cm_dummy", "gamedummy"])
# CMありをtreatment, CMなしをcontrolとする
treat = (data_df.cm_dummy == 1).tolist()
cv = (data_df.gamedummy == 1).tolist()
z = (data_df.Z == 1).tolist()
# train, test半分ずつに分ける
train_cv, test_cv, train_treat, test_treat, X_train, X_test, z_train, z_test = train_test_split(cv, treat, X, z, test_size=0.5, random_state=2)
# indexをリセット
X_train = X_train.reset_index(drop=True)
X_test = X_test.reset_index(drop=True)
# Z=1となる確率を予測するロジスティック回帰モデル構築
lr_z = LogisticRegression(C=0.01)
lr_z.fit(X_train, z_train)
# z-scoreの算出(z-score = 2P(Z=1|X) - 1)
z_score = 2 * lr_z.predict_proba(X_test) - 1
z_score = (z_score[:, 1]).tolist()
ここで結果を描画してみます。AUUCというのは今の所メジャーなupliftの評価指標で、uplift(青線)とbaseline(黄線)の間の面積で計算されます。
uplift(青線)は、横軸で表されるZ score rank以上の人のみに介入した時に、全く介入しなかった場合に比べてどれだけアプリ利用が増えるかを表しています。baselineは横軸で表されるz score rank以上の人にランダムに介入した時のupliftを表しています。
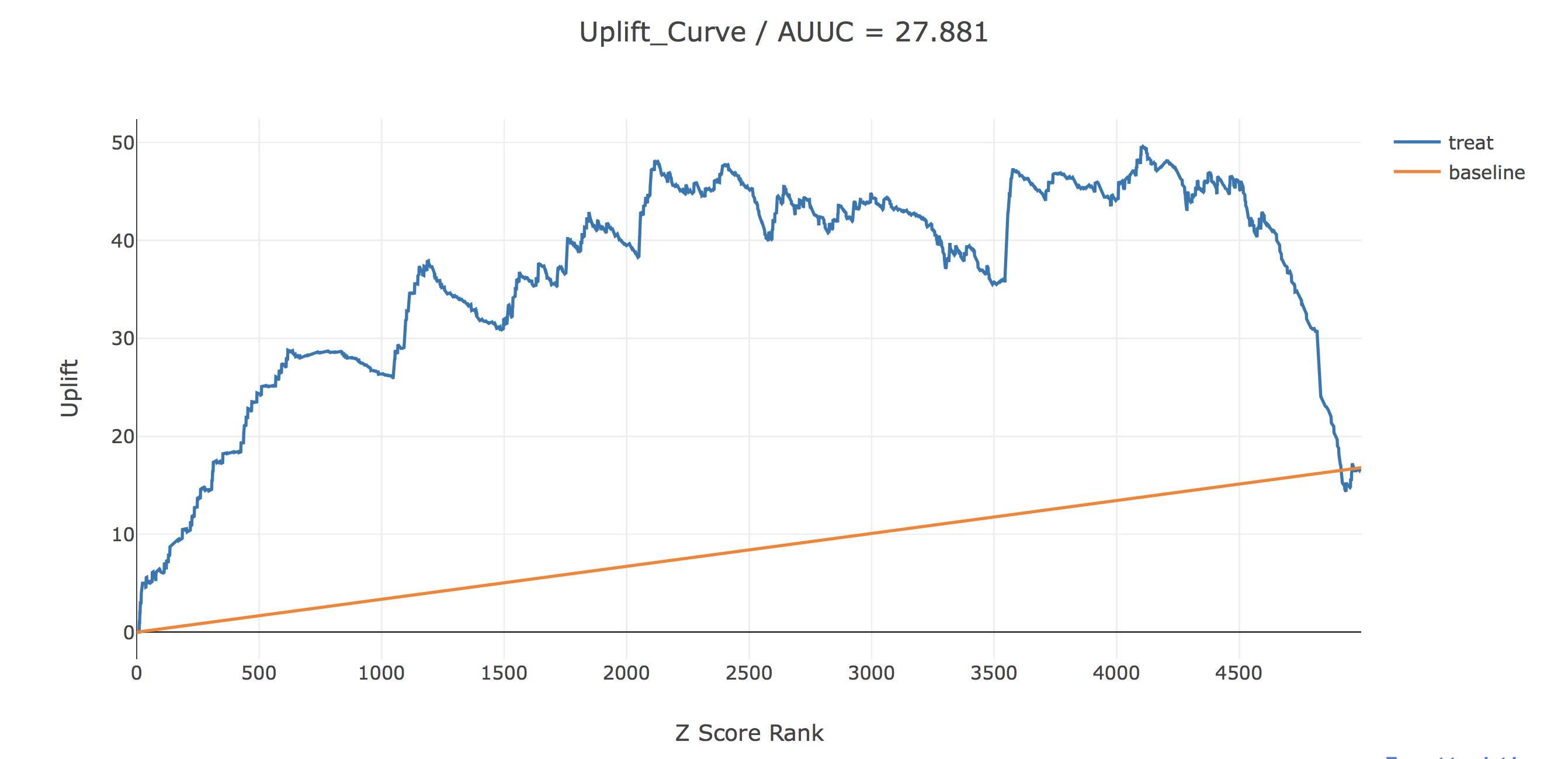
これを見てみるとある程度うまくいっているようにも見えます。Z score rankが上位約4100人に介入することで、介入しなかった場合よりも50人のアプリ利用を増やすことができそうです。また、ロジスティック回帰モデルの係数を見ることで、どの説明変数が介入効果を押し上げているかについて簡単に分析してみます。
### z-scoreを算出したロジスティック回帰モデルの係数を表示
for feature, coef in zip(X_test.columns, lr_z.coef_[0]):
print(f"{feature} / {round(coef, 4)}")
### これについては傾向スコアで補正した後の結果と比較
------------
child_dummy / 0.0239
area_kanto / -0.3468
area_tokai / 0.2823
area_keihanshin / 0.8965
T / 0.0027
F1 / 0.1595
F2 / -0.2699
F3 / -0.0892
M1 / 0.1931
M2 / 0.1633
------------
The Transformed Outcome Method
次に傾向スコアを用いたバイアス補正をした後にUplift Modelingをする手法であるThe Transformed Outcome Methodを試してみます。こちらは、前回記事『傾向スコアを用いて観察データからUpliftをモデリングする』にてメインで扱いましたね。
# データの読み込み
data_df = pd.read_csv('https://github.com/iwanami-datascience/vol3/raw/master/kato%26hoshino/q_data_x.csv')
data_df.head()
# 傾向スコアを求める
# 説明変数
cols_ = ["age", "sex", "TVwatch_day", "marry_dummy", "child_dummy", "inc", "pmoney",
"area_kanto", "area_tokai", "area_keihanshin",
"job_dummy1", "job_dummy2", "job_dummy3", "job_dummy4", "job_dummy5", "job_dummy6",
"fam_str_dummy1", "fam_str_dummy2", "fam_str_dummy3", "fam_str_dummy4"]
X_ = data_df[cols_].copy()
# 切片の導入
X_.loc[:, "Intercept"] = 1
# CM視聴有無ダミー
z1 = data_df.cm_dummy
# StatsModelsのLogitにより傾向スコアを推定
glm = sm.Logit(z1, X_)
result = glm.fit()
ps = result.predict(X_)
ps
------------
0 0.046217
1 0.255983
2 0.177427
3 0.227593
4 0.242373
------------
# Propensity Scoreで補正された目的変数を作成
data_df.loc[:, "ps"] = ps
data_df.loc[:, "adj_gamedummy"] = 0
data_df.loc[data_df.cm_dummy == 1, "adj_gamedummy"] = data_df.loc[data_df.cm_dummy == 1, "gamedummy"] / data_df.loc[data_df.cm_dummy == 1, "ps"]
data_df.loc[data_df.cm_dummy == 0, "adj_gamedummy"] = -data_df.loc[data_df.cm_dummy == 0, "gamedummy"] / (1 - data_df.loc[data_df.cm_dummy == 0, "ps"])
adj_z = data_df[["gamedummy", "adj_gamedummy"]]
# CMありをtreatment, CMなしをcontrolとする
treat = (data_df.cm_dummy == 1).tolist()
cv = (data_df.gamedummy == 1).tolist()
# train, test半分ずつに分ける
train_cv, test_cv, train_treat, test_treat, X_train, X_test, adj_z_train, adj_z_test = train_test_split(cv, treat, X, adj_z, test_size=0.5, random_state=2)
# indexをリセット
X_train = X_train.reset_index(drop=True)
X_test = X_test.reset_index(drop=True)
adj_z_train = adj_z_train.reset_index(drop=True)
adj_z_test = adj_z_test.reset_index(drop=True)
# ランダムフォレスト回帰を用いてadj_z_scoreを予測するモデルを構築(ただし、補正によりadj_z_scoreは連続変数となっているため回帰している)
rf = RandomForestRegressor(n_estimators=1000, max_depth=500)
rf.fit(X_train, adj_z_train.adj_gamedummy)
# 補正されたZ-Scoreを予測
adj_z_score = rf.predict(X_test)
ここでも先ほどと同じように、uplift(青線)は、横軸で表されるadj-Z score rank以上の人のみに介入した時に、全く介入しなかった場合に比べてどれだけアプリ利用者が増えるかを表しています。baselineは横軸で表されるuplift-score rank以上の人にランダムに介入した時のupliftを表しています。
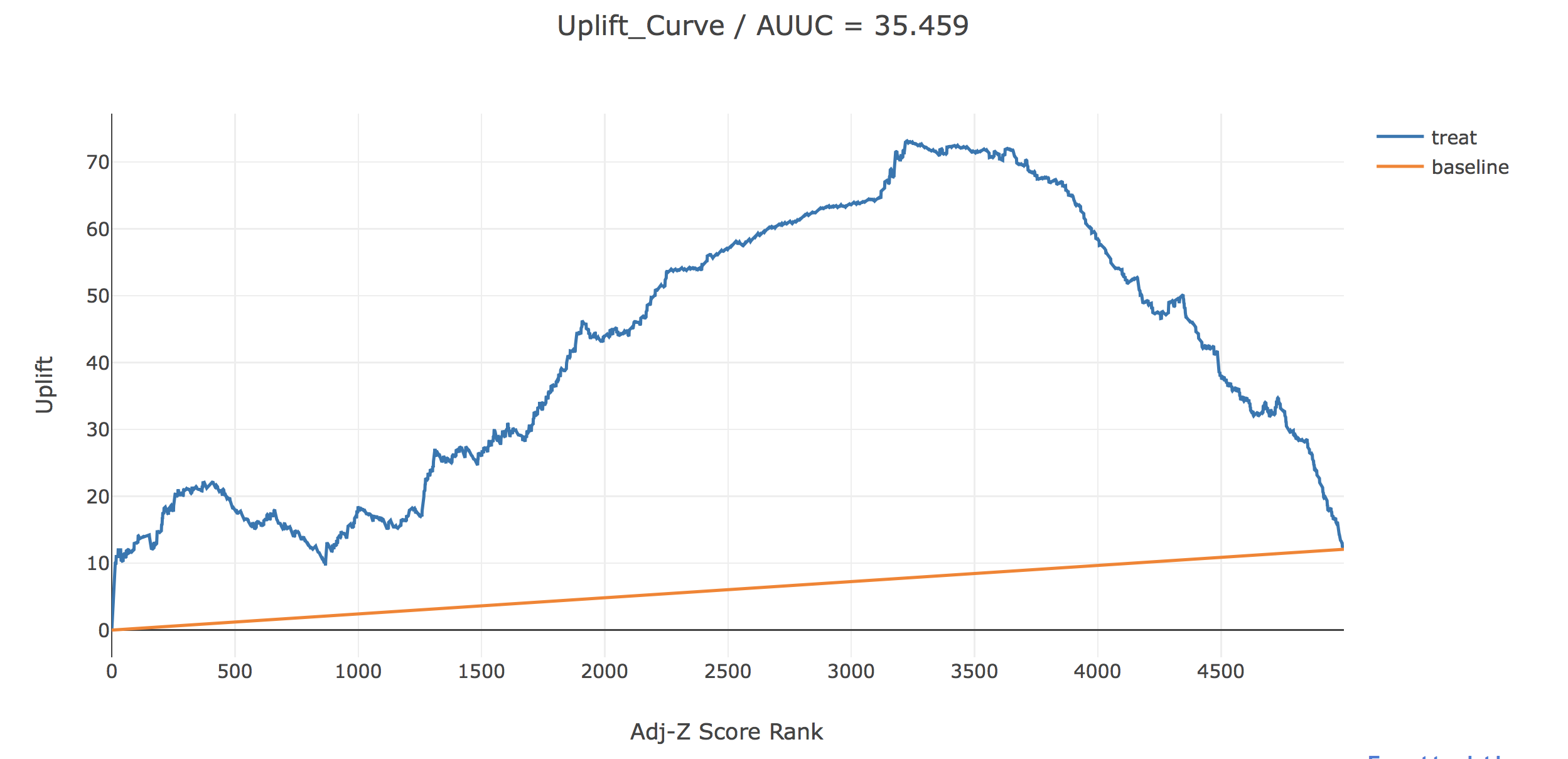
これを見るとAUUCが若干改善され、最大のUplfitも約73と改善されていることから、傾向スコアによる補正の効果はないことはないと思われます。しかし、アプリ利用率は傾向スコアで補正をする前から、CM視聴群の方がCM非視聴群よりも高かったことから前回やったアプリ利用時間に対するUplift Modelingよりは明快な結果が出にくかったと言えるかもしれません。さらにここでは、横軸にadj-Z scoreをとって描画してみます。

これをみて見ると、adj-z scoreが0以上、すなわち、個人介入効果が正であると予測された人たちに介入することでUpliftを最大化できそうという直感と整合的な結果にはちゃんとなっているようです。
また、先ほどと同じように、どの説明変数が介入効果を押し上げているかについて簡単に分析してみます。ただしここでは、adj-Z scoreの予測値を用いた説明変数で線形回帰することとします。
lr = LinearRegression()
for feature, coef in zip(X_train.columns, lr.coef_):
print(f"{feature} / {round(coef, 4)}")
------------
child_dummy / -0.0846
area_kanto / -0.0406
area_tokai / -0.0294
area_keihanshin / 0.0525
T / 0.2318
F1 / 0.0076
F2 / 0.0511
F3 / -0.0475
M1 / 0.0393
M2 / 0.1176
------------
もちろん先ほどとは、この係数の出し方が異なるので数字の大小を単純に比較することはできません。それでも、前回と同じように傾向スコアにより補正する前は、「子供有無ダミー」がCM視聴のアプリ利用に対する因果効果を増やすと推定されていますが、傾向スコアにより補正した後は、子供有無ダミー」がCM視聴のアプリ利用に対する因果効果を減らすと推定されています。ただそもそもの「子供有無ダミー」が持つCM視聴のアプリ利用に対する因果効果影響が、アプリ利用時間の時のそれよりも小さいと考えられる(子供がいてもいなくてもCMを見るとアプリを利用してみようと思う程度はそれほど変わらないが、子供がいないほうがその後のアプリ利用時間が増える)ため、今回は補正の有無により結果に大きな差が見られなかったのかもしれません。
さいごに
今回は、傾向スコアを用いてバイアスを補正することによって観察データにおける分類問題に対してUplift Modelingを適用してみました。データの性質上、前回よりはわかりにくい結果となりましたが、それでもバイアス補正によりある程度の効率化は可能なようです。また、このような傾向スコアによる補正は(今回のデータに関しては)分類問題に対して適用しても特に大きな問題は起こりませんでした。
参考
[1] Athey, S and Imbens, G. Machine Learning Method for estimating heterogeneous causal effects. stat, 1050:5, 2015
[2] Gutierrez, P and Gerardy, J, Y. Causal Inference and Uplift Modeling A review of the literature. JMRL: Workshop and Conference Proceedings 67:1-13, 2016