- This is the article of the C++ Advent Calendar 2014 DAY 24
glm - グラフィックスプログラミングのためのC++数学系ライブラリー
glm とは何か?
ここで紹介する glm は C++ の座標系ベクターの取り扱いを中心とした数学系のライブラリーです。基本的には3DCG向けの、特にOpenGLとの親和性の高いグラフィックス用途のライブラリーですが、その機能はよく整理されて実装されており、比較的低次のベクター処理に汎用に扱えるものとなっています。
今回は C++ Advent Calendar 2014 への参加記事として、 glm について簡単にその凡その機能について紹介したいと思います。
glm の公式情報と入手、ライセンスについて
glm の公式ウェブサイトはこちら:
-
http://www.g-truc.net/ - Christophe Riccio による OpenGL 情報ウェブサイト "g-truc"
- http://glm.g-truc.net/ - g-truc の主要コンテントとなった glm の公式ウェブサイト
入手は github から:
- https://github.com/g-truc/glm - git@github.com:g-truc/glm.git
ライセンスは The Happy Bunny License と MIT License で提供されています。以下は readme.txt より引用:
GLM is licensed under The Happy Bunny License and MIT License
- The Happy Bunny License
- MIT License
ライセンスの要点は軍事目的に使わなければ著作権表示を守って自由に使って良いという具合です。(実用にあたってはその時点でのライセンス文書を正確に確認して下さい。)
glm をはじめて使う: Hello, glm!
(※開発環境が整っていない、あるいはどう整えて良いか分からない状態の方は、 Cloud9 IDE などログインしてすぐに使える状態の開発環境を試してみると良いでしょう。Cloud9 IDEを使う場合は中身はUbuntuですから不足があればsudo apt-getで環境へ導入できます。)
先ず、プロジェクトのリポジトリーを用意しましょう。
mkdir -p ~/repos/hello_glm
cd ~/repos/hello_glm
git init
git submodule add git@github.com:g-truc/glm.git submodule/glm
(※この時点で何をしているのか分からない場合には、それぞれのコマンドやgitの使用方法について先に学びましょう。)
glm を使った初歩的なプログラムを書いてみましょう。
vim main.cxx
(※vimで編集するのに慣れていなければお好みの、あるいは Cloud9 IDE のエディター機能など使うと良いでしょう。)
# include <iostream>
# include <glm/glm.hpp>
auto main()
-> int
{
auto a = glm::vec2( 3, 4 );
std::cout
<< "a: " << a.x << " " << a.y << "\n"
<< "length(a): " << glm::length( a )
;
}
このソースコードでは glm の基礎的な機能である glm::vec2 (2次元ベクター)を a として定義し、標準出力へ定義された a の値 .x と .y を出力、ついでに glm::length (ベクターの長さを求める関数)により a の長さを出力します。
さっそく翻訳して実行結果を確認したいところかと思いますが、直接c++ -I./submodule/glm main.cxx -o hello_glm && hello_glmとする代わりに、早々に CMakeLists.txt を用意してモダンでクロスプラットフォームな開発リポジトリーにしましょう。
vim CMakeLists.txt
cmake_minimum_required(VERSION 2.8.12)
project(hello_glm)
if("${CMAKE_SOURCE_DIR}" STREQUAL "${CMAKE_BINARY_DIR}")
message(SEND_ERROR "In-source builds are not allowed.")
endif()
set(CMAKE_DISABLE_IN_SOURCE_BUILD ON)
set(CMAKE_DISABLE_SOURCE_CHANGES ON)
set(CMAKE_VERBOSE_MAKEFILE ON)
set(CMAKE_COLOR_MAKEFILE ON)
if (WIN32)
set(CMAKE_SHARED_LIBRARY_PREFIX "")
endif()
if(CMAKE_CXX_COMPILER MATCHES "/em\\+\\+(-[a-zA-Z0-9.])?$")
set(CMAKE_CXX_COMPILER_ID "Emscripten")
endif()
if(NOT CMAKE_CXX_COMPILER_ID STREQUAL "MSVC")
include(CheckCXXCompilerFlag)
CHECK_CXX_COMPILER_FLAG("-std=c++11" COMPILER_SUPPORTS_CXX11)
CHECK_CXX_COMPILER_FLAG("-std=c++0x" COMPILER_SUPPORTS_CXX0X)
if(COMPILER_SUPPORTS_CXX11)
set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -std=c++11")
elseif(COMPILER_SUPPORTS_CXX0X)
set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -std=c++0x")
else()
message(STATUS "The compiler ${CMAKE_CXX_COMPILER} has no C++11 support. Please use a different C++ compiler.")
endif()
set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -std=c++11 -Wall -pedantic-errors")
else()
set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} /Wall /Za")
endif()
include_directories(${CMAKE_SOURCE_DIR}/submodule/glm)
file(GLOB CXX_SOURCE_FILES *.cxx)
if(NOT CMAKE_CXX_COMPILER_ID STREQUAL "Emscripten")
set(TARGET ${PROJECT_NAME})
else()
set(TARGET ${PROJECT_NAME}.html)
endif()
add_executable(${TARGET} ${CXX_SOURCE_FILES})
(※但し今回の執筆前後、著者はMSVC++でテストしていません。著者の予想外の事が起きたらごめんなさい、その時にはコメントなど頂けると嬉しいです。)
このCMakeLists.txtは必要最小限ではなく、比較的に実用的な内容で記述してあります。もし、わからない事があれば調べてみてcmakeをある程度使いこなせるようになると良いでしょう。
では、ビルドしましょう。
mkdir build
cd build
cmake .. -G Ninja -DCMAKE_BIULD_TYPE=Debug
(※ビルドツールを-D Ninjaとしていますが、cmakeはNinjaのほか、Makefile CodeBlocks Eclipse CDT KDevelop Sublime Text それから Xcode や MSVC++ にも対応しているはずなので必要に応じて選択すると良いでしょう。 )
ninja
(※Makefileならmake、他のビルドツールを選択した場合はそれぞれのビルド方法に従います。)
実行してみましょう。
./hello_glm
a: 3 4
length(a): 5
二次元のカルテシアン座標系で (x,y)=(3,4) のベクターを a としましたので、 glm::length(a) は直角を挟む2辺の長さがそれぞれ 3、 4 の直角三角形の斜辺の長さという事になります。小学校の算数の教科書にも直角三角形の辺の長さが整数になる組み合わせとして掲載されている図形です。
glm の機能と構造の概要
glm は次のような機能と構造になっています。仮想的にC++ソースコード風に示します。
// A.1. glm ライブラリーの一部機能は CPP を定義して制御できるようになっています。
# define GLM_SWIZZLE
// 1. glm ライブラリーの基本機能が含まれます。
# include <glm/glm.hpp>
// 2. glm ライブラリーの拡張機能のうち既に仕様が安定した機能が glm/gtc に含まれます。
# include <glm/gtc/constants.hpp>
// 3. glm ライブラリーの拡張機能のうち試験的に実装されている機能が glm/gtx に含まれます。
# include <glm/gtx/color_space.hpp>
// 4. glm ライブラリーの拡張機能をひとまとめに取り込みたい場合には glm/ext.hpp を使います。
# include <glm/ext.hpp>
auto main()
-> int
{
// glm ライブラリーの機能は基本的には glm 名前空間に定義されます。
glm::vec2 a, b;
}
// glm は C++ ヘッダーオンリーライブラリーとして提供されているため、
// 翻訳時にヘッダーファイルが取り込まれていれば
// バイナリーライブラリーのリンクなどは必要ありません。
glm の基礎的な機能: glm::vec, glm::mat の使い方
glm には基礎的な機能として glm::vec と glm::mat があり、それぞれ低次元のベクターとマトリックスの実装となっています。
これらはテンプレートにより float double long double std::uint32_t などへの特殊化版もこの後で紹介する各種の glm の多くの機能も含めて使用できるように定義されています。
もし、std::uint16型の glm::vec3 を使いたい時には、
glm::u16vec3 a( 1, 2, 3 );
など明示的に glm::u16vec3 を使用します。具体的な型には他に、 glm::i32vec3 glm::u64vec3 glm::f64vec3 などの選択肢があり、IEEE754/Binery(32|64)、std::u?int(8|16|32|64)_t の内部型のそれぞれの対応版が実装されています。
(※正確には OpenGL 規格の型に準拠できるように出来ていますが、固定小数点など現在一般的なCPUでネイティブに扱えない型は使用できません。)
注意点として、glm::vec3( 1, 2, 3 ) はデフォールトで glm::f32vec3 となり、整数型にしたい場合は型の明示が必要です。
glm::vec の使用例:
# include <iostream>
# include <glm/glm.hpp>
auto main()
-> int
{
auto p = glm::vec4( 2, 3, 4, 5 );
auto q = glm::vec4( 3, 4, 5, 6 );
// 四則演算の演算子が定義済みで便利に使えます。
// operator+ の例:
auto n = p + q;
// operator* は単なる次元毎のスカラー積です:
auto m = p * q;
std::cout
<< "n ( operator+ ): " << n.x << " " << n.y << " " << n.z << " " << n.w << "\n"
<< "m ( operator* ): " << m.x << " " << m.y << " " << m.z << " " << m.w << "\n"
;
}
n ( operator+ ): 5 7 9 11
m ( operator* ): 6 12 20 30
glm の vec の各次元の要素の値には、次元毎に x y z w の順に、あるいは r g b a でアクセスできます。
glm::mat の使用例:
# include <iostream>
# include <glm/glm.hpp>
// あとで gtx 拡張の紹介でも簡単に触れます。glm::to_string()を使えるようになります。
# include <glm/gtx/string_cast.hpp>
auto main()
-> int
{
glm::mat4 m;
std::cout << glm::to_string( m ) << "\n";
m *= 3.14f;
std::cout << glm::to_string( m ) << "\n";
}
mat4x4((1.000000, 0.000000, 0.000000, 0.000000), (0.000000, 1.000000, 0.000000, 0.000000), (0.000000, 0.000000, 1.000000, 0.000000), (0.000000, 0.000000, 0.000000, 1.000000))
mat4x4((3.140000, 0.000000, 0.000000, 0.000000), (0.000000, 3.140000, 0.000000, 0.000000), (0.000000, 0.000000, 3.140000, 0.000000), (0.000000, 0.000000, 0.000000, 3.140000))
さすがに 4x4 マトリックスのダンプをちまちまと表示するのは面倒なので #include <glm/gtx/string_cast.hpp> を使ってそこは手抜きをしました。これについては後ほど拡張機能の解説でも簡単に触れます。
glm::mat4 は glm::mat4x4 への別名で、これもまた glm::vec4 の例と同じように glm::f32mat4x4 が実体となります。他に、 glm::mat2 glm::mat3 もあり、それぞれ 2x2 と 3x3 に対応し、さらに glm::mat4x3 など行と列が一致しない組み合わせについても定義があります。
演算子のオーバーロードは float を全ての要素に積算する例を示しました。この手の演算子は glm::vec4 と同様に使えます。
vec と異なる性質として、vec ではデフォールトの構築子で生成されるオブジェクトが 零ベクターとなりますが、 mat では単位行列になる点に注意が必要かもしれません。しかしこれは実用上は寧ろ便利でありがたい事が多いでしょう。
ちなみに、個別の要素へのアクセスは以下のように行います。
# include <iostream>
# include <glm/glm.hpp>
# include <glm/gtx/string_cast.hpp>
# include <type_traits>
auto main()
-> int
{
glm::mat4 m;
m[0][1] = 1.73f;
for ( auto a = 0; a < 4; ++a )
for ( auto b = 0; b < 4; ++b )
std::cout << m[a][b] << " ";
std::cout
<< "\n"
<< glm::to_string( m ) << "\n"
<< *( reinterpret_cast< float* >( &m ) + 1 )
;
}
1 1.73 0 0 0 1 0 0 0 0 1 0 0 0 0 1
mat4x4((1.000000, 1.730000, 0.000000, 0.000000), (0.000000, 1.000000, 0.000000, 0.000000), (0.000000, 0.000000, 1.000000, 0.000000), (0.000000, 0.000000, 0.000000, 1.000000))
1.73
注意点として、この結果からもさり気なく分かるように、 glm の mat は行優先(Row-Major Order)のメモリー配置を取ります。
glm::vec glm::mat のメモリー表現
glm::vec と glm::mat は厳密にはいわゆる POD 型ではありませんが、標準配置型(standard layout type)なので、 std::vector<glm::vec4> として OpenGL や Direct3D で GPU のバッファーへ転送する基データを生成したり、あるいは struct my_vertex { glm::vec4 position; glm::vec3 normal; glm::vec2 texcoord0; }; std::vector<my_vertex> の様に扱っても通常は安全です。
# include <iostream>
# include <type_traits>
# include <glm/glm.hpp>
auto main()
-> int
{
std::cout
<< std::boolalpha
<< "pod : " << std::is_pod<glm::vec4>::value << "\n"
<< "standard layout: " << std::is_standard_layout<glm::vec4>::value << "\n"
<< "trivial : " << std::is_trivial<glm::vec4>::value
;
}
pod : false
standard layout: true
trivial : false
注意点として、以下のような派生型の使い方をすると標準配置型の性質は失われ、仮想関数テーブルの為にサイズもデータ本体に必要な容量からは異なる事になります。これは恐らく OpenGL や Direct3D のバッファーへの転送では扱えないか、トリックが必要になり面倒の種になるでしょう。
struct vertex { glm::vec3 position; virtual auto f() -> void { }; };
struct vertex_ex1: vertex { glm::vec3 normal; };
struct vertex_ex2: vertex_ex1 { glm::vec2 texcoord0; };
std::cout
<< std::boolalpha
<< "vertex : " << std::is_standard_layout<vertex>::value << " " << sizeof(vertex) << "\n"
<< "vertex_ex1: " << std::is_standard_layout<vertex_ex1>::value << " " << sizeof(vertex_ex1) << "\n"
<< "vertex_ex2: " << std::is_standard_layout<vertex_ex2>::value << " " << sizeof(vertex_ex2) << "\n"
;
vertex : false 24
vertex_ex1: false 32
vertex_ex2: false 40
glm の標準・拡張機能の紹介
glm には標準機能に加え gtc と gtx の二段階の拡張機能実装があり、拡張機能はそれぞれ必要に応じて個別に #include するか、あるいはまとめて glm/ext.hpp を #include して使います。
ここからは glm ライブラリーに含まれる便利な機能について、幾つか紹介します。
標準機能でできるようになる便利な計算機能たち
glm は名前の由来である OpenGL Mathematic の名前からも想像が付いたかもしれませんが、特に GLSL で言語標準として提供される多くの便利機能の C++ 実装を含んでいます。例えば lerp とか clamp とか。
以下で紹介する機能は glm/glm.hpp を #include すれば一通り使用可能になる現在のバージョンでは既にコア機能として実装されています。
以下、アルファベット順に紹介します。
絶対値: glm::abs(x)
std::cout << glm::to_string( glm::abs( glm::vec3( 1, -1, -3 ) );
vec3(1.000000, 1.000000, 3.000000)
<cmath> に含まれる std::abs では glm::vec3 に対しては使えませんが、 glm::abs を使うと目的を簡単に達成できます。もちろん、単なる float にも気兼ね無く使えます。
std::abs に対する glm::abs のような実装は他の glm 名前空間に定義される関数でも同様に glm::vec3等へ適用可能な実装になっていて便利に使えます。
天井値: glm::ceil(x)
std::cout << glm::to_string( glm::ceil( glm::vec2( M_PI, -M_PI ) ) );
vec2(4.000000, -3.000000)
抑え込み: glm::clamp(x, min, max)
std::cout << glm::clamp( M_PI * 2, 0.0, M_PI / 2 );
1.5708
<cmath>には無いが、しばしばプログラミングで要求される事の多い clamp は値を [min-max] の範囲に抑え込みます。丸め込み(rounding)では無く抑え込み(clamp)です。
浮動小数点数の整数型表現を取得 : floatBitsToInt( f ) floatBitsToUint( f )
std::cout << std::hex << glm::floatBitsToUint( 1 );
3f800000
これは IEEE754/Binary32 等の浮動小数点数型のメモリー表現について知識が無いとやや謎めいた機能に見えるかもしれません。
float型の値に対してメモリーアドレスを取り*reinterpret_cast<std::int32_t*>としても同じ結果が得られるでしょう。浮動小数点数をビットレベルで制御したい場合に必要となる、用途のやや特殊な機能で、 glm::intBitsToFloat glm::uintBitsToFloat と対になる機能です。一般には必要になる事は稀かもしれません。
床値: floor(x)
std::cout << glm::to_string( glm::floor( glm::vec2( M_PI, -M_PI ) ) );
vec2(3.000000, -4.000000)
天井値(ceil)と対になる床値(floor)です。 ceil では同様の引数で vec2(4.000000, -3.000000) が得られていましたが、 floor では vec2(3.000000, -4.000000) が得られています。
名前の通り、これらは値を整数へ丸め込むに当たり天井側へ丸め込むか、床側へ丸め込むか、という関数になります。もちろん、こちらも vec ではなく単純な float の値へ適用する事もできます。
融合積和算 : fma(a, b, c)
言葉で表面上の結果について言えば、 f(b) = a * b + c を計算するだけの関数です。このFMA(Fused Multiply-Add)演算とわざわざ名前がついて関数まで用意されている理由は、計算機の浮動小数点数の計算の実装方法に起因します。
現在一般的なPCでこの FMA 演算を効率よく本当にCPU命令レベルで実行できるのは intel の AVX 拡張命令セットに含まれる FMA 命令ををサポートした比較的最近のCPUのみです。(いわゆるスーパーコンピューター向けのCPUでは対応製品があります。)一方、GPU では FMA 命令は頻出する重要な命令として、 OpenGL GLSL でも 4.0 から組み込みの関数として使用できるようになりました。 Direct3D HLSL にも同様の組み込み関数があります。
しかしながら、今の所は glm::fma を使用した C++ コードを記述して、 AVX 命令をサポートするCPU向けにビルドしたとしても、 VFMADDSS 命令へ intrinsics 等で翻訳される事はありません。
float f( const float a, const float b, const float c )
{ return a * b + c; }
この関数は clang++-3.5 -O0 では以下のような命令コード群に翻訳されました:
0x00000000004008b0 <+0>: push %rbp
0x00000000004008b1 <+1>: mov %rsp,%rbp
0x00000000004008b4 <+4>: movss %xmm0,-0x4(%rbp)
0x00000000004008b9 <+9>: movss %xmm1,-0x8(%rbp)
0x00000000004008be <+14>: movss %xmm2,-0xc(%rbp)
0x00000000004008c3 <+19>: movss -0x4(%rbp),%xmm0
0x00000000004008c8 <+24>: mulss -0x8(%rbp),%xmm0
0x00000000004008cd <+29>: addss -0xc(%rbp),%xmm0
0x00000000004008d2 <+34>: pop %rbp
0x00000000004008d3 <+35>: retq
XMMレジスターとSSE命令にはなっていますが単純に mulss addss を行っているだけです。
続いて、clang++-3.5 -O3 -march=native で翻訳すると以下の様になりました:
0x00000000004008c0 <+0>: vmulss %xmm1,%xmm0,%xmm0
0x00000000004008c4 <+4>: vaddss %xmm2,%xmm0,%xmm0
0x00000000004008c8 <+8>: retq
XMMレジスターを使いながらも AVX 命令セットの vmulss と vaddss 使ってくれましたが、 vfmaddss は使ってくれませんでした。
念の為、以下のような自動ベクター化を期待しやすい関数も翻訳してみました:
void f( const float* a, const float* b, const float* c, float* r )
{
for( auto n = 0; n < 256; ++n )
r[n] = a[n] * b[n] + c[n];
}
0x0000000000400800 <+112>: vmovups (%rdi,%rax,4),%ymm0
0x0000000000400805 <+117>: vmovups 0x20(%rdi,%rax,4),%ymm1
0x000000000040080b <+123>: vmovups 0x40(%rdi,%rax,4),%ymm2
0x0000000000400811 <+129>: vmovups 0x60(%rdi,%rax,4),%ymm3
0x0000000000400817 <+135>: vmulps (%rsi,%rax,4),%ymm0,%ymm0
0x000000000040081c <+140>: vmulps 0x20(%rsi,%rax,4),%ymm1,%ymm1
0x0000000000400822 <+146>: vmulps 0x40(%rsi,%rax,4),%ymm2,%ymm2
0x0000000000400828 <+152>: vmulps 0x60(%rsi,%rax,4),%ymm3,%ymm3
0x000000000040082e <+158>: vaddps (%rdx,%rax,4),%ymm0,%ymm0
0x0000000000400833 <+163>: vaddps 0x20(%rdx,%rax,4),%ymm1,%ymm1
0x0000000000400839 <+169>: vaddps 0x40(%rdx,%rax,4),%ymm2,%ymm2
0x000000000040083f <+175>: vaddps 0x60(%rdx,%rax,4),%ymm3,%ymm3
0x0000000000400845 <+181>: vmovups %ymm0,(%rcx,%rax,4)
0x000000000040084a <+186>: vmovups %ymm1,0x20(%rcx,%rax,4)
0x0000000000400850 <+192>: vmovups %ymm2,0x40(%rcx,%rax,4)
0x0000000000400856 <+198>: vmovups %ymm3,0x60(%rcx,%rax,4)
AVX 命令が微妙に変わっていますが、 vmulps と vaddps で -ss が -ps にベクター化されただけでした。ちなみに、 intel 命令セットのSIMD命令系の末尾の ss は scalar single precision 、 ps は packed single precision で、お察しの通り、64bit浮動小数点数型では sd とか pd になります。また、 V で始まっている命令は AVX 、 命令のまんなかに入っている mul add mov などが 積算 加算 移動(CPUレジスターとメインメモリー間の、など)です。
今回は SIMD 命令のはなしではないのでこのくらいにして glmの 機能に戻りましょう。
仮数 : fract( f )
std::cout << glm::fract( M_PI );
0.141593
fract は浮動小数点数の仮数部(fraction)のみを抽出します。IEEE754形式の浮動小数点数では、値を符号部、指数部、仮数部に分け、それぞれに一定の容量を割り当てて記録します。このうちの仮数部のみを抽出した浮動小数点数を取得します。通常、より単純に言うと、浮動小数点数の小数点の後ろの部分のみを得られます。どうしてそうなるのか理解したい方は IEEE754/Binary32 の「けち表現」の項について知識を補充すると良いでしょう。
例では M_PI を与えたので、 .141593 が出力として得られました。もちろん、これは std::cout へ出力した際に丸められた表示で実際に保持している値の精度は IEEE754/Binary32 でももう少しだけ高いです。
指数部と仮数部の分離 : glm::frexp( f, e )
これは執筆時点でどうも動作しないようなので、 ほぼ等価な <cmath> 版の紹介に留めます。
int e;
auto x = std::frexp( M_PI, &e);
std::cout
<< M_PI << " = " << x << " x std::exp2( " << e << ")" << "\n"
<< " = " << ( x * std::exp2( e ) )
;
3.14159 = 0.785398 x std::exp2( 2)
= 3.14159
与えた浮動小数点数、例では M_PI を、 x = exp2( e ) を満たす x を関数のリターン、 e を関数の第2引数で受けた実体参照に対して記録します。事実上の動作としては任意の浮動小数点数 M_PI を与えて上記等式を満たす x と e を取得する関数で、IEEE754で言う指数部と仮数部をそれぞれ取得する事と等価です。
注意点として、 std::frexp では &e として int* を渡していますが、 glm::frexp 版は OpenGL GLSL の frexp との互換性を重視している事もあり、 第2引数は int& を与えるシグニチャーとなっています。
整数型を浮動小数点数へ変換 : intBitsToFloat uintBitsToFloat
std::cout
<< std::hex << glm::floatBitsToUint( M_PI ) << "\n"
<< glm::uintBitsToFloat( 0x40490fdbu )
;
40490fdb
3.14159
前出の floatBitsToInt floatBitsToUint の逆の操作を行います。つまり、整数型のメモリー表現をそのまま reinterpret_cast<float*> して再解釈した浮動小数点数値を取得します。
こうした機能は、例えば効率的に浮動小数点数を生成する乱数エンジンの実装の様に、生成した乱数ビット列を一定の値の範囲、例えば unorm 値([0.0-1.0])に整えたい場合などに必要と成り得るような、ごく低レベルの処理です。必要が無ければ無闇に使わない方が良いでしょう。また、 C++ では OpenGL GLSL と違い union を使う事で型の再解釈キャストを避けた実装も可能でしょう。
無限大の判定 : isinf( f )
std::cout << std::boolalpha << glm::isinf( M_PI / 0 );
true
与えられた値が無限大であれば true を返す。
非数の判定 : isnan( f )
std::cout << std::boolalpha << glm::isinf( 0. / 0 );
true
与えられた値が非数であれば true を返す。
指数部と仮数部から浮動小数点数を生成 : ldexp( x, e )
frexp の逆関数に相当する ldexp ですが、対になる frexp 同様に ldexp も glm 版は動作確認できなかったので std 版で実装を紹介します。
std::cout << std::ldexp( 0.785398f, 2 );
3.14159
内部的には frexp で紹介した様に float ldexp( float f, int e ) { return x * std::exp2( e ); } と等価の処理を行います。
(次元毎の)最大値 : glm::max( a, b )
glm::vec3 a( 1, 7, -M_PI );
glm::vec3 b( 2, 3, std::cos(M_PI) );
std::cout << glm::to_string( glm::max( a, b ) );
vec3(2.000000, 7.000000, -1.000000)
std::max のように単に float を比較する事もできます。例の様に vec を与えた場合には、各次元毎に求めた最大値を採用した a b と同じ次元数の vec を返します。各次元に何を扱うかはユーザー次第なので、何らかの属性群の理想的な最大値構成を評価するのに使っても良いでしょうし、色のRGB値の合成処理に使っても良いでしょう。
(次元毎の)最小値 : glm::min( a, b )
glm::vec3 a( 1, 7, -M_PI );
glm::vec3 b( 2, 3, std::cos(M_PI) );
std::cout << glm::to_string( glm::min( a, b ) );
vec3(1.000000, 3.000000, -3.141593)
glm::max と対になる glm::min です。次元毎の最小値からなるスカラーないしベクターを取得します。
線形合成 : glm::mix( x, y, a )
std::cout
<< glm::to_string( glm::mix( a, b, 4. / 5 ) );
vec3(1.800000, 3.800000, -1.428319)
x と y について線形合成を混合比 a で行った結果を取得します。 a が 0.0 の時 x 、 a が 1.0 の時 y を得られます。
これは C++ 標準には無いけれど一般に使いどころの多い便利な機能です。同種の合成系の機能実装として glm::lerp や glm::slerp も使いどころではとても便利の良い機能です。
(負数や浮動小数点数対応の)剰余算 : glm::mod( x, y )
std::cout
// 480 [degrees] => 120 [degrees]
<< glm::mod( M_PI * 8 / 3 , M_PI * 2 ) << "\n"
// -270 [degrees] => 90 [degrees]
<< glm::mod( -M_PI * 3 / 2 , M_PI * 2 )
;
2.0944
1.5708
浮動小数点数 x を y で剰余算した結果を取得します。
注意点として、よく似た機能の std::fmod とも std::remainder とも効果が異なります。
| 関数 | 得られる結果 |
x/yの結果から整数を得る処理方法 |
|---|---|---|
glm::mod |
x - std::ceil( x / y ) * y |
正の無限大方向へ丸める(rounding toward plus infinity; RP) |
std::fmod |
x - ( x > 0 ? std::ceil( x / y ) : std::floor( x / y ) ) * y |
0に近くなるように丸める(rounding toward zero; RZ) |
std::remainder |
x - std::round( x / y ) * y |
IEEE754-1985 準拠 |
glm の実装で整数部を ceil で丸めているのは例によって OpenGL GLSL に準拠している事によります。この ceil で丸める挙動の場合は例示したような角度の回転を正規化したい場合に便利が良くなります。
例示では角度の単位系をラジアンとしたので日常的な度数法に慣れていると分かり難いかもしれません。以下に、浮動小数点数である意味はほぼ無い整数的にもきりの良い値とはなりますが、度数法でのそれぞれの挙動の違いも示しておきます。
std::cout
<< glm::mod ( -45.f, 360.f ) << "\n"
<< glm::fmod ( -45.f, 360.f ) << "\n"
<< glm::remainder( -45.f, 360.f ) << "\n"
<< ( -45 % 360 ) <<
;
315
-45
-45
-45
整数部と少数部の分離 : glm::modf( x, i )
glm::vec2 x( M_PI, -M_PI );
glm::vec2 i;
std::cout << glm::to_string( glm::modf( x, i ) ) << "\n";
std::cout << glm::to_string( i );
vec2(0.141593, -0.141593)
vec2(3.000000, -3.000000)
x の整数部を参照で受けた i へ、小数部をリターンで取得します。
std 版との違いは OpenGL GLSL と同様に呼び出しコードとしては扱える様に glm 版では i を参照で受けます。 std 版は <cmath> の C 互換機能という事もありポインターを渡す仕様です。また、 glm 版では vec を渡して一度にまとめて複数の次元の modf 結果を取得できるようになっています。
最近傍の整数への丸め : glm::round( x )
glm::vec2 x( M_PI, -M_PI );
std::cout << glm::to_string( glm::round( x ) ) << "\n";
vec2(3.000000, -3.000000)
0.5 を丸めた際の挙動は実装依存。丸め処理については端数処理#コンピュータでの丸め を、また FE_DOWNWARD FE_TONEAREST FE_TOWARDZERO FE_UPWARD は std::round には寄与しない事にも注意が必要な事もあるかもしれません。
最近傍の整数への偶数丸め : glm::roundEven( x )
glm::vec4 x( -1.5, -0.5, 0.5, 1.5 );
std::cout << glm::to_string( glm::roundEven( x ) ) << "\n";
vec4(-2.000000, 0.000000, 0.000000, 2.000000)
round では実装依存の .5 はどちら側へ丸めるべきかを偶数に定めたバージョン。環境によらず確実に最近傍の偶数側の整数へ丸められる。環境依存により丸め方向が異なっては困る再現性の重要で繊細な処理が必要な際には round よりも roundEven を使うべき状況もあるかもしれません。
符号を取得 : glm::sign( x )
glm::vec4 x( -1.5, -0.5, 0.5, 1.5 );
std::cout << glm::to_string( glm::sign( x ) ) << "\n";
vec4(-1.000000, -1.000000, 1.000000, 1.000000)
「符号部」では無く「符号」を取得する。
注意点として、よく似た <cmath> の機能 std::signbit とは挙動が異ります。 glm::sign は名前通りに「符号」を取得するのに対し、 std::signbit はこちらも名前通りに「符号部(値の型に対応した符号部の1ビット)」を取得します。
クリッピングされたエルミート補間値の取得 : glm::smoothstep( e1, e2, x )
glm::vec4 e1( 0, 0, 0, 0 );
glm::vec4 e2( 100, 100, 100, 100 );
glm::vec4 x( -20, 20, 40, 120 );
std::cout << glm::to_string( glm::smoothstep( e1, e2, x ) ) << "\n";
vec4(0.000000, 0.104000, 0.352000, 1.000000)
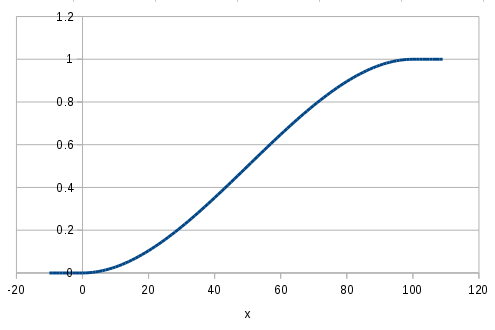
e1 を始点、 e2 を終点として入力値 x を与えた際のエルミート補間(Hermite interpolation)値を [0.0-1.0] で取得します。 x が e1 と e2 の範囲外にある場合は glm::clamp され、 0.0 または 1.0 が得られます。
エルミート補間は少しだけ予備知識が無いとピンと来ないかもしれません。そこで、具体的に e1 = 0 e2 = 100 を与えた glm::smoothstep の、入力値 x に対する出力結果を以下に図示しておきます。
smoothstep の名前通り、始点から終点へと滑らかな段差を実現したい場合に役立ちます。段差を作るのが目的という事もあり、範囲外の入力値は glm::clamp 挙動となります。
ちなみに "Hermite" がヘルミートやハーミットではなく、その由来の "Charles Hermite" がチャールズ・ハーミットではなくシャルル・エルミートと素敵な感じの音になるのはフランス語の発音体系に起因します。
閾値による判定 : glm::step
glm::vec4 e( 20, 20, 20, 20 );
glm::vec4 x( 0, 10, 20, 30 );
std::cout << glm::to_string( glm::step( e, x ) ) << "\n";
vec4(0.000000, 0.000000, 1.000000, 1.000000)
閾値 e に対して、入力値 x のデジタルな応答(0 または 1)を得ます。より正確には return x < e; を取得します。
まったく補間せずに、ある閾値に応じて処理のON/OFFや値の切り替えを行いたい場合に使用します。
零方向への丸め : glm::trunc( x )
glm::vec4 x( -1.5, -0.5, 0.5, 1.5 );
std::cout << glm::to_string( glm::trunc( x ) ) << "\n";
vec4(-1.000000, -0.000000, 0.000000, 1.000000)
ceil や floor など丸め関数の仲間で、零方向の最近傍の整数に丸めます。
CPP定義によって発効する機能
要素への柔軟なアクセス : #define GLM_SWIZZLE
これは CPP を定義すると使えるようになる便利機能で、これを定義してから glm/glm.hpp を "#include" すると次のように .xyzw() .xyz() zzww() .rgb() .bgra() のように任意の要素の順序d並べ替えた vec を手軽に扱える様になります。
# include <iostream>
# define GLM_SWIZZLE
# include <glm/glm.hpp>
# include <glm/gtx/string_cast.hpp>
auto main()
-> int
{
glm::vec4 a( 1, 2, 3, 4 );
auto b = a.zwyx();
auto c = a.rgb();
std::cout
<< glm::to_string( a ) << "\n"
<< glm::to_string( b ) << "\n"
<< glm::to_string( c ) << "\n"
;
}
デフォールトの浮動小数点数モデルの変更
OpenGL GLSL では以下のようにしてデフォールトの精度を変更できます:
precision mediump int;
precision highp float;
glm ではこれを CPP 定義で行えます。
# define GLM_PRECISION_MEDIUMP_INT;
# define GLM_PRECISION_HIGHP_FLOAT;
# include <glm/glm.hpp>
特に明示しなければ float 系、 double 系、 int 系、 uint系 の vec や mat は全て GLSL でいうところの High precision 相当に設定されます。
翻訳時のおしゃべり機能
いわゆる verbose モード的に翻訳時にどのヘッダーが読まれたとか、命令セットをサポートしているかなどを #pragma message により出力させる事ができます。
# define GLM_MESSAGES
# include <glm/glm.hpp>
一度試してみると分かりますが、通常はデフォールトの出力無効状態の方が心臓にも良いかもしれません。
C++言語規格レベルの強制
glm のコードを何れのC++言語規格向けに設定するか強制できます。
# define GLM_FORCE_CXX14
# include <glm/glm.hpp>
この例では C++14 に強制します。他に、 C++11 C++98 への強制を設定できます。
SIMDサポートの強制
通常 glm は標準で自動的に判断して SIMD 命令をある程度積極的に使おうとしてくれます。この自動判断を無効化し特定のSIMDサポートを強制する事ができます。
// vec4 mat4 を SIMD 向けにします。
// 内部的に __mm128 なんかを使う事になります。
# define GLM_GTX_simd_vec4
# define GLM_GTX_simd_mat4
// SIMD命令セットを強制します。
# define GLM_FORCE_SSE2
# define GLM_FORCE_SSE3
# define GLM_FORCE_SSE4
# define GLM_FORCE_AVX
# define GLM_FORCE_AVX2
// SIMD 命令を使いたく無い場合に誤って
// GLM_GTX_simd_vec4 など明示されていた場合にエラーを出力するようにします。
# define GLM_FORCE_PURE
インライン化
パフォーマンスを最大限に優先したい場合にはインライン化を明示的に指示できます。
# define GLM_FORCE_INLNIE
# include <glm/glm.hpp>
gtc 拡張機能群
種々の定数: glm/gtc/constants.hpp
# include <glm/gtc/constatns.hpp>
std::cout
<< glm::pi<double>() << "\n"
<< glm::e<double>() << "\n"
<< glm::three_over_two_pi<double>() << "\n"
;
3.14159
2.71828
4.71239
π e π * 3 / 2 などの定数値を指定の型で取得できます。ただ、この機能については constexpr 非対応な事もあり、 Sprout の sprout::math::pi などを使った方が嬉しい事もあるかもしれません。
使用可能な定数の一覧は、ドキュメントのGLM_GTC_constants をどうぞ。
マトリックスの積による射影変換: glm/gtc/matrix_transform.hpp
特に Computer Graphics 界隈ではお馴染みの同次座標による射影変換を扱える様になります。
# include <glm/gtc/matrix_transform.hpp>
glm::vec3 p0;
std::cout << glm::to_string( p0 ) << "\n";
auto translation = glm::translate( glm::mat4(), glm::vec3( 0, 0, 1 ) );
std::cout << glm::to_string( ( translation * glm::vec4( p0, 1 ) ).xyz() ) << "\n";
auto rotation = glm::rotate( glm::mat4(), float(M_PI) / 4, glm::vec3( 1, 0, 0 ) );
std::cout << glm::to_string( ( rotation * translation * glm::vec4( p0, 1 ) ).xyz() ) << "\n";
vec3(0.000000, 0.000000, 0.000000)
vec3(0.000000, 0.000000, 1.000000)
vec3(0.000000, -0.707107, 0.707107)
例で紹介した glm::translate と glm::rotate の他に glm::scale もあります。例では零ベクター p0 を、Z軸方向に +1 だけ移動し、その後に X 軸回転を π / 4 だけ回転しています。
glm は OpenGL との親和性の強いライブラリーで、射影変換の際に glm::mat4 の積を行う順序も同様です。これは Direct3D と OpenGL では 行列に対して座標を扱うベクターが「列ベクター(OpenGL)」か「行ベクター(Direct3D)」かに起因し、両方の API を使う必要があったり、一方の API から他方の API へと鞍替えする際に混乱する事があります。注意しましょう。
ノイズ生成器 : glm/gtc/noise.hpp
- シンプレックス・ノイズ (Simplex noise)
# include <fstream>
# include <glm/glm.hpp>
# include <glm/gtc/noise.hpp>
auto main()
-> int
{
std::ofstream o("simplex.pgm");
o << "P2\n256 256\n255\n";
for ( auto y = 0; y < 256; ++y )
{
for ( auto x = 0; x < 256; ++x )
o << glm::roundEven( ( glm::simplex( glm::vec2( x / 64., y / 64. ) ) + 1.0f) * 255 / 2 ) << " ";
o << "\n";
}
}
シンプレックス・ノイズは 2001 年に次に紹介するパーリン・ノイズのケン・パーリン(Ken Perlin)がパーリン・ノイズの次元増加に伴うオーバーヘッドの増大を改善しつつ同様のノイズを生成する目的で発表したノイズ生成器です。
シンプレックス・ノイズではそれまでのパーリン・ノイズでは生成コストが次元 n の増加に伴い、 Ο( pow( 2, n ) ) で増加する点を Ο( n, 2 ) に改善しています。例示は絵として分かり良いので2次元で生成しましたが、4次元以上のノイズを生成する際にはパーリン・ノイズ以上の生成速度が得られます。
命名の「シンプレックス」は日本語にしてしまうと意味が曖昧になってしまうと感じたので私の翻訳ポリシーには珍しく「単体」と訳語を充てませんでした。数学的な日本語の「単体」はある次元における次元数+1の凸正多面体のようなものらしい。
ちなみに、例示したプログラムのコードでは画像ファイルを PNM 形式で生成しています。これはテキストファイル形式で画像を表現する形式の1つで、ちょっとしたデータのダンプを画像として出してみたい時に重宝します。著者は普段 Linux のデスクトップ環境としてお馴染みの KDE を使っていて、画像は gweinview というソフトウェアで表示して見ています。もしかしたら Windows や OSX の標準的な環境では PNM 形式を画像として表示できないかもしれません。その時は .pbm .pgm .ppm などの PNM 形式に対応した画像ビューアーを探すか、或いはサンプルプログラムの例を Magick++ にするなど適当に扱い易いデータ出力形式にすると良いです。それほど大きな画像分解能でなければ文字列で値を出力して表計算ソフトの可視化機能を使って確認してみても良いでしょう。
- パーリン・ノイズ(Perlin noise)
# include <fstream>
# include <glm/glm.hpp>
# include <glm/gtc/noise.hpp>
auto main()
-> int
{
std::ofstream o("perlin.pgm");
o << "P2\n256 256\n255\n";
for ( auto y = 0; y < 256; ++y )
{
for ( auto x = 0; x < 256; ++x )
o << glm::roundEven( ( glm::perlin( glm::vec2( x / 8., y / 8. ) ) + 1.0f) * 255 / 2 ) << " ";
o << "\n";
}
}
パーリン・ノイズ は先に紹介したシンプレックス・ノイズより昔、1983年にケン・パーリンが発表したノイズ生成器で、それと知らなくとも多くの人がこのノイズ生成器の、或いは生成されたノイズのお世話になっています。例えば雲のテクスチャーとして使われたりする例は有名です。
四元数(クォータニオン) : glm/gtc/quaternion.hpp
glm::vec3 p0( 0, 0, 1 );
glm::quat q1( glm::vec3( M_PI / 2, 0, 0 ) );
glm::quat q2( glm::vec3( 0, M_PI / 2, 0 ) );
auto p1 = q1 * p0;
auto p2 = q2 * p0;
auto p3 = glm::slerp( q1, q2, .5f ) * p0;
std::cout
<< glm::to_string( p1 ) << "\n"
<< glm::to_string( p2 ) << "\n"
<< glm::to_string( p3 )
;
vec3(0.000000, -1.000000, 0.000000)
vec3(1.000000, 0.000000, 0.000000)
vec3(0.666667, -0.666667, 0.333333)
ジンバルロック(Gibmal lock)フリーの3次元空間での回転制御でお馴染みの四元数(クォータニオン; quaternion)です。
glm::quat の構築子に直接 x y z w と4つの四元数の要素を与えて直接的に構築する事も出来ますが、利便性から glm::quat( glm::vec3( ) ) として、カルテシアン座標系におけるX軸回転、Y軸回転、Z軸回転をそれぞれ glm::vec3( x, y, z ) で与えてそれを素に glm::quat を生成して扱う事が殆どでしょう。
例では、点 p0 を X軸に π/2(90°)回転した p1 、 Y軸に π/2 回転した p2 、それから、 四元数 q1 と q2 を球面補間でちょうど中間の位置に合成した四元数で回転した p3 を生成して、それぞれのベクターの各次元の値を表示しています。
ここで、しれっと glm::slerp(a,b,x) を使っていますが、これは glm::mix の四元数用のオーバーロードの中身として追加定義され、つまり球面補間により a と b を合成比 x で合成します。線形補間の glm::lerp の球面補間版と言うわけです。
ちなみに、ベクターに対して例のように簡単にクォータニオンを適用できるように演算子がオーバーロードされていますし、計算コストも単純には増加する事から使う機会は微妙かもしれませんが、glm::mat4_cast( q ) として四元数 glm::quat を回転行列 glm::mat4 へ変換できます。また、その逆の変換用に glm::quat_cast( m ) もこの拡張で使えるようになります。
gtx 拡張機能
色空間の変換 : glm/gtx/color_space.hpp
auto rgb = glm::vec3( 0.5, 0.5, 0.25 );
auto hsv = glm::hsvColor( rgb );
std::cout << glm::to_string( hsv );
vec3(60.000000, 0.500000, 0.500000)
現在の glm コア実装の vec では rgba 系を想定したメンバーの定義しかありませんが、値としては同じ次元数で HSV 系の色空間も扱えます。 gtx/color_space を使うと、glm::hsvColor と glm::rgbColor が追加され、RGB色空間からHSV色空間、HSV色空間からRGB色空間への変換を扱えるようになります。
注意点として、例の結果のように、 glm::hsvColor の結果得られる H 値(色相; Hue)は度数法になっている点です。
文字列型へ変換 : glm/gtx/string_cast.hpp
std::cout
<< glm::to_string( glm::vec4() ) << "\n"
<< glm::to_string( glm::mat4() )
;
vec4(0.000000, 0.000000, 0.000000, 0.000000)
mat4x4((1.000000, 0.000000, 0.000000, 0.000000), (0.000000, 1.000000, 0.000000, 0.000000), (0.000000, 0.000000, 1.000000, 0.000000), (0.000000, 0.000000, 0.000000, 1.000000))
ここまでにも vec と mat の値の確認として手抜きの為に使ってきた glm::to_string です。glm::quat 未対応だったりするのが少々残念なところですが、あるものは便利に使いましょう。
OpenGL 非推奨互換 API の提供
OpenGL は特に近年の進化の過程で多くの API の仕様変更、そして非推奨や廃止を伴いました。特にマトリックス系の API は消え去る運命にあります。例えば glPushMatrix と glPopMatrix 、それからハードウェアT/L 時代の名残りのライティング、 glBegin と glEnd などなど。
巻き込まれる形で一般に有用で、 Direct3D でも当然 D3DX に入っているような機能も消えます。そこで、 glm ではそれら古い OpenGL が提供していた有用な API の一部を glm ライブラリーの vec や mat を使うことで実装しています。
これらは Computer Graphics 用途でしか使う機会が無いかもしれませんが、その用途では有用というか、およそ必須です。
- 射影変換関連 (
glm/gtc/matrix_transform.hpp)-
glRotate=>glm::rotate()// 回転 -
glScale=>glm::scale()// 拡大縮小 -
glTranslate=>glm::translate()// 平行移動 -
glFrustum=>glm::frustum// 透視投影 -
glOrtho=>glm::ortho// 正射影
-
- 他の行列関連の機能
-
glLoadIdentity=>glm::mat4()// 単位行列 -
glMultMatrix=>glm::mat4::operator*()// 積 -
glLoadTransposeMatrix=>glm::transpose()// 転置
-
加えて、 GLU の機能も glm の vec と mat で扱える様になっています。
- 射影変換関連 (
glm/gtc/matrix_transform.hpp)-
gluLookAt=>glm::lookAt()// ビュー変換 -
gluOrtho2D=>glm::ortho()// 正射影 -
gluPerspective=>glm::perspective()// 透視投影 -
gluPickMatrix=>glm::pickMatrix()// スクリーン座標からのピッキング -
gluProject=>glm::project()// ワールド座標からスクリーン座標を取得 -
gluUnProject=>glm::unProject()// スクリーン座標からワールド座標を取得
-
翻訳時間への配慮
glm はテンプレートをそれなりに使っている事もあり、翻訳には少しだけ時間が掛かるかもしれません。Boostに比べるとどうという事はありませんが、気になる場合には前方宣言と定義本体の分離機構を glm-0.9.5 から使えるようになっています。
// ヘッダーファイルでは前方宣言のみ扱う
# include <glm/fwd.hpp>
// ソースファイルでは定義本体を扱う
# include <glm/glm.hpp>
少々翻訳速度を改善できるかもしれません。
ほかには?
とりあえず、 glm のマニュアルを見ましょう。これでも 1/3 以上は説明をすっ飛ばしたり、gtc/gtxについては基礎的で分かりやすい所や有用なものをピックアップして紹介しました。
マニュアルにもほんのり概要程度と、それから gtx の事はほとんど書かれていないので、 Doxygen とあとはソースコードを直接読んで使いましょう。ともあれ、そこまで全て使いきろうとしなくても、 glm はとても有用な比較的に低次の vec 、 mat の実行時処理ライブラリーで、ポリシーもしっかりとして安心できるものに育っています。この紹介記事がどこかの趣味でゲームを作りたい人や、或いはどこかの研究室の学生さんの初動の助けなどにでもなれば幸いです。
質問があれば
著者はふだんQiitaをあまり良く使ってはいませんし、頂いたご質問に的確な答えを素早く対応できるとも限りません(恐らく)。もし、この記事のエラッタのご指摘では無く、比較的に純粋に glm や C++ や Computer Graphics あるいは何からの関連した事柄について疑問が湧き自分では簡単には解決の糸口も見つけられないようなら、是非 StackExchange デビューするきっかけにすると良いかもしれません。最近は日本語版の StackOverflow(JA) もオープンベータとしてサービスが始まりましたし、英語が苦手でも臆することはありません。
とは言え、少なくとも現状では、できれば英語版のいわゆる本家と言われる StackExchange 系の StackOverflow(EN) や GameDevelopment(EN) を頼ると、質問の答えやヒントが既にたくさんあるかもしれません。それでもしも英語がわからずに答えの意味を掴みきれない事があれば、日本語版でそのQAの日本語での紹介を依頼するのも良いでしょう。集団的知性(Collective wisdom)はあなたの味方で、私もまたおそらくその味方の一人となることもあるでしょう。そしてあなたの質問もまた、後の誰かの疑問への答えとなる事でしょう。
(※訳: すたっくおーばーふろー便利だな)
あとがき
今年はちょっとしたMMORPGのフレームワークを最近のC++やライブラリー事情で構築する事例を紹介しようかと企んでいましたが、それほど時間的な余裕も取れませんでしたので glm の紹介記事としました。
glm はOpenGLで3DCGを扱う際には必須と言える優れたライブラリーの1つですが、特に3DCGという用途に限らずとも実装、性能も良く、便利に汎用的に扱えるシーンもあるかと思います。この紹介が、広く誰かしらの助けとなる事があれば幸いです。