たまには真面目なめも。より詳しくは最後にあげる文献やWebページを見てください。
ある人の身長と体重というようなデータを得たときに、これら2変量の間に関係があるのかということに興味があるとします。2つの変数間の解析では、回帰分析をやればいいんでしょ、ふんふん🎵などと単純に考えていると痛い目にあうことがあります。一口に線形回帰といっても、解析の目的に応じてとるべき手法が変わってくるためです。
まず分析の目的が、ある変数から別の変数を予測することにあるのか、今回のように片方の変数ともう片方の変数との関係を知りたいのかが大きな違いとなります。これらはの分析手法は観測データの性質により、それぞれ線形回帰の$I$型、$II$型の模型に分けられます。
線形回帰におけるI型回帰とII型回帰
I型の回帰
2変数(説明変数$X$と目的変数$Y$)の関係を調べる際、通常見かける回帰の方法です。$I$型の回帰ではつぎの4つの仮定から成り立っています(Skall & Rohlf (藤井訳) 1983)。
- 説明変数$x$は誤差を伴わない($x$は固定されている)
- ある与えられた$X$の値に対する変数Yの期待値は、一次関数 $\mu y = \alpha x + \beta$で表される
- 変数Xのある与えられた値$x_i$に対して、$Y$は独立に、かつ正規分布する
- 変数は等分散する
例のような生物のデータでは、これらの仮定を満たすことができていません。まず、測定した身長と体重において、説明変数を身長、目的変数に体重を考えたとき、説明変数である身長の測定誤差を無視することはできない(身長と同様、生活習慣や家庭環境というような個体差が生じる)ため、はじめの「説明変数$X$は誤差を伴わない」が成り立ちません。加えてそもそも論として、身長が体重の直接的な原因となるわけではない、という問題があります。これらの関係は、身長(原因)による体重(効果)への影響ではなく、単純な変数間の関係を示すのが適当です。
II型の回帰
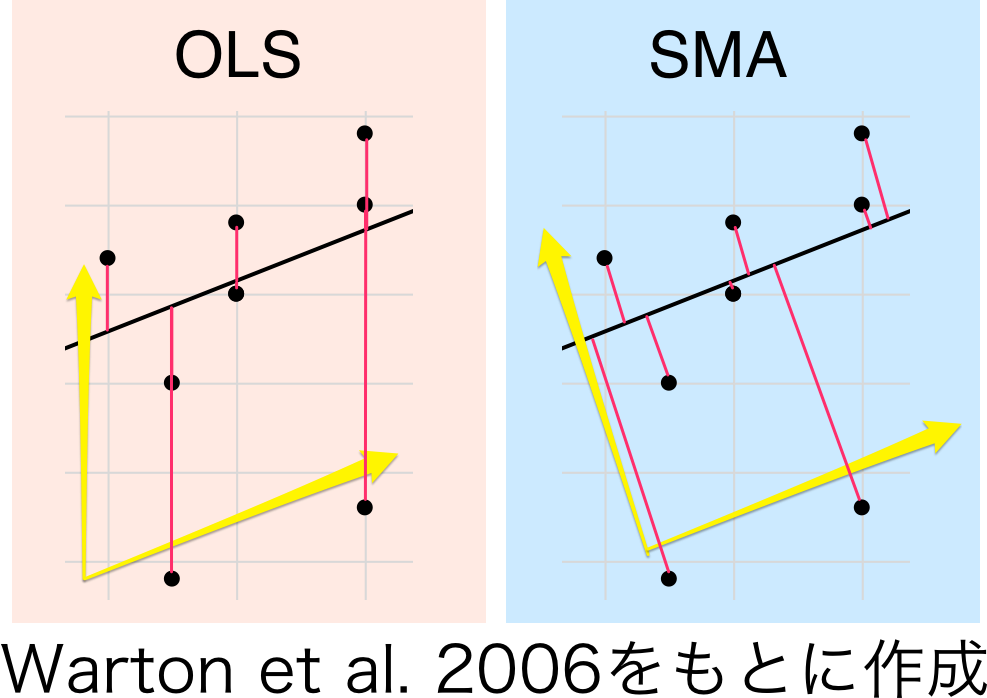
2変量間の関係をみたい場合には、相関を調べるのが一つの方法ですが、時としてこれらの関数的な関係を知りたい場合があります。$I$型回帰が成立しない状況においては、$II$型の回帰が有効な分析手法となります。説明変数Xの誤差を考慮しない$I$型回帰に対し、$II$型回帰では目的変数$Y$, 説明変数$X$どちらの変数の誤差も考慮します。例でいえば、身長も体重も測定したときの個体に依存した誤差があるだろう、と仮定するわけです(考えみれば当然?)。
(OLSでは目的変数の誤差のみ、SMAでは両変数の誤差を含む)
例題: プロ野球選手(投手)の身長と体重の関係
身長と体重のデータが手元になかったので「プロ野球データFreak」から投手の身長と体重(元データはプロ野球選手名鑑とかでしょうか)とってきます。身長ランキングの上位100人分の選手名、所属チーム、そして身長と体重のデータです(細かいことなんかは餅屋に任せたい。セイバーメトリクスとか知らないし)。
# 使用パッケージ(II型回帰のためのパッケージはあとで)
library(ggvis)
library(rvest)
library(dplyr)
library(broom)
url <- "http://baseball-data.com/ranking-height/all/p.html"
url %>% html() %>%
html_nodes("table") %>% .[[1]] %>%
html_table() %>%
dplyr::rename(name = 選手名,
team = チーム,
height = 身長,
weight = 体重) %>%
select(name, team, height, weight) %>%
mutate_each(funs(extract_numeric), height, weight) -> df
str(df)
# 'data.frame': 100 obs. of 4 variables:
# $ name : chr "ミコライオ" "オンドルセク" "クロッタ" "ポレダ" ...
# $ team : chr "楽天" "ヤクルト" "日本ハム" "巨人" ...
# $ height: num 205 203 201 198 198 198 198 196 196 196 ...
# $ weight: num 115 104 107 109 105 88 121 100 100 104 ...
summary(df)
# name team height weight
# Length:100 Length:100 Min. :186.0 Min. : 72.00
# Class :character Class :character 1st Qu.:187.0 1st Qu.: 85.00
# Mode :character Mode :character Median :188.0 Median : 90.00
# Mean :189.5 Mean : 91.43
# 3rd Qu.:191.0 3rd Qu.: 95.25
# Max. :205.0 Max. :121.00
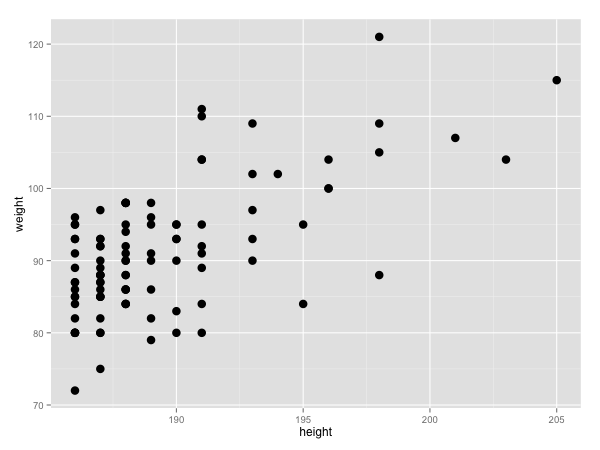
高身長の上位は助っ人選手が多いですね。200cm以上の選手は以外と少ない...。
なにはともあれ、まずはデータを散布図で示すところからはじめます。
df %>% ggplot(aes(height, weight)) +
geom_point(size = 4) -> p
p
なにやら相関関係がありそうなのでこれらの2変数の相関係数を見てみます。
df %$% cor.test(height, weight) %>% tidy() %>% kable()
| estimate | statistic | p.value | parameter | conf.low | conf.high |
|---|---|---|---|---|---|
| 0.6351581 | 8.140716 | 0 | 98 | 0.5012776 | 0.7393388 |
~~ここちょっと消えてますね... p.valueという値があったんですが...。~~というわけで、相関係数r = 0.6351581(P = 0.000000000001269651)が得られました。
最小二乗法
単回帰での回帰直線を引く方法である最小二乗法のおさらいです。
最小二乗法は各データの残差の二乗和を最小にすることで求まりますが、ここの残差(誤差の推定量)は$I$型回帰の場合、$Y$つまり垂直のみの誤差となります。というのも、$I$型回帰は説明変数であるXは固定されていることを仮定しているためです。例題での最小二乗法により求めた傾きと切片はつぎのようになります。
df %$% lm("weight ~ height", data = .) %>% tidy() %>% kable(format = "html")
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -178.479388 | 33.1625799 | -5.381951 | 0.0000005 |
| height | 1.424474 | 0.1749814 | 8.140716 | 0.0000000 |
では$II$型回帰での最小二乗法ではどうなるかみてみましょう。Rでは$II$型回帰を実施する関数を含んだパッケージがlmodel2とsmatrの2つがあります。両パッケージも$II$型回帰のMA, SMAに対応しています(今回はSMAを採用)。今回はそれを確認することも含めて両パッケージで実施します。
library(lmodel2)
library(smatr)
df %>% lmodel2("weight ~ height", data = .) -> res.model2
res.model2$regression.results[3, ] %>% kable()
| Method | Intercept | Slope | Angle (degrees) | P-perm (1-tailed) | |
|---|---|---|---|---|---|
| 3 | SMA | -333.5184 | 2.242708 | 65.96841 | NA |
df %>% sma("weight ~ height", data = .) -> res.sma
res.sma %$% as.data.frame(coef) %>% kable(format = "html")
| coef.SMA. | lower.limit | upper.limit | |
|---|---|---|---|
| elevation | -333.518369 | -399.331571 | -267.705167 |
| slope | 2.242708 | 1.922187 | 2.616677 |
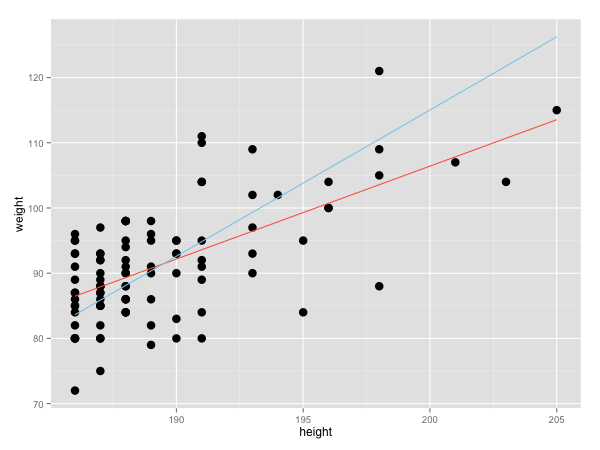
$II$型回帰では$X,Y$どちらの誤差も扱うため、$I$型回帰よりも傾きがきつくなる傾向になります。
最後に$I$型と$II$型による直線回帰引いてみて比較します。赤色の線が$I$型、青色の線が$II$型回帰です。
log_data <- res.sma$log
a <- res.sma$coef[[1]][1, 1]; b <- res.sma$coef[[1]][2, 1]
p + stat_smooth(method = "lm", se = FALSE, colour = "tomato") + # OLS
stat_function(fun = function(x) {a + x * b}, colour = "skyblue") # SMA
今回は、生物のデータでありがちな$X, Y$どちらの変数にも誤差があるときの回帰分析の方法について扱いました。実際は、$II$型回帰の種類もさまざまで、データの性質や用途に応じて使い分けるのが良いです(Legendre 2013)。また、$II$型回帰における処理や種の違い(傾き)を比較する方法についてはまた余力があるときに書きたいと思います。
さいごに、Warton (2006)では、既存の回帰分析の問題を取り上げ、$II$型回帰の分析手法について説明しています。lmodel2のvignettesとして提供されているLegendre (2013)では、$II$型回帰の応用例と使い分けの基準が書かれています。もっと勉強しておかないと...
参考
- Warton, D. I., Wright, I. J., Falster, D. S., & Westoby, M. (2006). Bivariate line-fitting methods for allometry. Biological Reviews, 81(02), 259. doi:10.1017/S1464793106007007
- Warton, D. I., R. A. Duursma, D. S. Falster, and S. Taskinen. 2012. smatr 3- an R package for estimation and inference about allometric lines. Methods in Ecology and Evolution 3:257–259.
- Sokal, R. R. & Rohlf, F. J. 藤井宏一訳 (1983). 生物統計学. 共立出版
- Legendre, L. (2013). Model II Regression User Guide
- 粕谷英一 (1998). 生物学を学ぶ人のための統計のはなし 君にも出せる有意差. 文一総合出版
- 第一回広島ベイズ塾・最小二乗法
- 飯島の雑記帳 - 統計解析ログ/Ⅱ型の回帰分析