この記事は数値計算 Advent Calendar 2018の6日目の記事です。
※ 12/9に未完部分を加筆しました。
1. はじめに
偏微分方程式を解くことは数値計算の大きなテーマの一つです。そもそも解析的に解の得られない方程式も多く、簡単な方程式でも境界条件が複雑だとやはり手計算では手に負えない問題になります。
そんな場合に数値計算は強力な手段となります。偏微分方程式の数値解法には様々なものがありますが、本記事ではその中でも基本的な有限差分法 (finite difference method, FDM) を使って、偏微分方程式の中の双曲型 (hyperbolic) と呼ばれるタイプを解く方法について簡単に紹介します。
2. 双曲型偏微分方程式とは
2-1. 定義
$N$ 個の独立変数を並べたベクトル $\mathbf{U}$ と $N \times N$ の行列 $\mathbf{A}$ に対し、以下のような方程式系を考えます。
\frac{\partial\mathbf{U}}{\partial t}
+ \mathbf{A}\frac{\partial\mathbf{U}}{\partial x}
= \mathbf{0}
このときに、行列 $\mathbf{A}$ が $N$ 個の実固有値を持ち、それに対応して $N$ 個の線型独立な固有ベクトルを持つ場合、この方程式系を双曲型 (hyperbolic) といいます。
これは空間1次元の場合ですが、例えば3次元なら
\frac{\partial\mathbf{U}}{\partial t}
+ \mathbf{A}\frac{\partial\mathbf{U}}{\partial x}
+ \mathbf{B}\frac{\partial\mathbf{U}}{\partial y}
+ \mathbf{C}\frac{\partial\mathbf{U}}{\partial z}
= \mathbf{0}
となり、この3つの行列 $\mathbf{A}, \mathbf{B}, \mathbf{C}$ それぞれについて上の性質が成り立つかどうかを考えます。
このように行列を使った形式を非保存形 (non-conservative form) といい、一方で以下のような形式を保存形 (conservative form) といいます。
・1次元の場合
\frac{\partial\mathbf{U}}{\partial t}
+ \frac{\partial\mathbf{F(U)}}{\partial x}
= \mathbf{0}
・3次元の場合
\frac{\partial\mathbf{U}}{\partial t}
+ \frac{\partial\mathbf{F(U)}}{\partial x}
+ \frac{\partial\mathbf{G(U)}}{\partial y}
+ \frac{\partial\mathbf{H(U)}}{\partial z}
= \mathbf{0}
この $\mathbf{F(U)}$ 等をフラックス (flux) と呼びます。なぜ保存形かというと、この表式は保存則を表す式 (e.g., 流体の連続の式、電磁気学の電荷保存の式) の一般化とみなせるからです。
この保存形も $\mathbf{F(U)}$ のヤコビアン $\mathbf{A} = \partial\mathbf{F}/\partial\mathbf{U}$ によって非保存形に変換され、これを用いて同様に双曲型かどうかを考えることができます。
本記事では主に1次元の非保存形について考え、拡散項やソース項等は扱いませんが、より複雑な場合に対してもここでの考え方が基礎になると思います。
2-2. 双曲型偏微分方程式の基本的性質
さて、双曲型方程式の解は大雑把に言って"波"状であるという特徴があります。
簡単のため線形の場合を考え、行列 $\mathbf{A}$ を以下のように対角行列 $\mathbf{\Lambda}$ に対角化します。
\mathbf{A} = \mathbf{K}\mathbf{\Lambda}\mathbf{K}^{-1}\\
\mathbf{\Lambda} = \mathbf{K}^{-1}\mathbf{A}\mathbf{K}
したがって、新しいベクトル $\mathbf{W} = \mathbf{K}^{-1}\mathbf{U}$ を導入すると、方程式は
\frac{\partial\mathbf{W}}{\partial t}
+ \mathbf{\Lambda}\frac{\partial\mathbf{W}}{\partial x}
= \mathbf{0}
となり、 $N$ 個の実固有値 $\lambda_1, \lambda_2, ..., \lambda_N$ と $\mathbf{W} = \left[W_1, W_2, ..., W_N\right]$ によって、方程式は以下の $N$ 個の独立な移流方程式に変形されます。
\frac{\partial W_l}{\partial t} + \lambda_l \frac{\partial W_l}{\partial x} = 0, (l = 1, 2, ..., N)
ここから $W_1, W_2, ..., W_N$ がそれぞれ速度 $\lambda_1, \lambda_2, ..., \lambda_N$ で伝播することがわかります。つまりこの固有値は方程式を特徴付ける速度ということになるので、これを特性速度 (characteristic speed) と呼びます。非線形の場合はこのような簡単な変形はできませんが、特性速度は同様に定義されます。
2-3. 双曲型偏微分方程式系の例
これだけではあまり実感がわかないと思うので、この表記法に慣れるためにも幾つか例を挙げてみます。
・真空中のマクスウェル方程式 (電磁波)
\mathbf{U} = \begin{bmatrix}
E_y \\
B_z
\end{bmatrix},
\mathbf{A} = \begin{bmatrix}
0 & c^2 \\
1 & 0
\end{bmatrix} \\
\lambda_1 = c, \lambda_2 = -c
($E_y$ : $y$ 方向の電場, $B_z$ : $z$ 方向の磁場, $c$ : 真空中の光速)
・浅水方程式 (浅水波)
\mathbf{U} = \begin{bmatrix}
u \\
\eta
\end{bmatrix},
\mathbf{A} = \begin{bmatrix}
0 & g\\
h & 0
\end{bmatrix} \\
\lambda_1 = \sqrt{gh}, \lambda_2 = -\sqrt{gh}
($u$ : $x$ 方向の速度, $\eta$ : 波高, $g$ : 重力加速度, $h$ : 水深)
・オイラー方程式 (音波)
\mathbf{U} = \begin{bmatrix}
\rho \\
p \\
u
\end{bmatrix},
\mathbf{A} = \begin{bmatrix}
u & 0 & \rho \\
0 & u &\gamma p \\
0 & 1/\rho & u
\end{bmatrix} \\
\lambda_1 = u, \lambda_2 = u+c_s, \lambda_3 = u-c_s \\
c_s = \sqrt{\frac{\gamma p}{\rho}}
($\rho$ : 密度, $p$ : 圧力, $u$ : $x$ 方向の速度, $\gamma$ : 比熱比, $c_s$ : 音速)
・MHD方程式 (Alfvén波)
\mathbf{U} = \begin{bmatrix}
\rho \\
B_y \\
u \\
\end{bmatrix},
\mathbf{A} = \begin{bmatrix}
u & 0 & \rho \\
0 & u & B_y \\
0 & B_y/\mu_0\rho & u
\end{bmatrix} \\
\lambda_1 = u, \lambda_2 = u+v_A, \lambda_3 = u-v_A \\
v_A = \frac{B_y}{\sqrt{\mu_0\rho}}
($\rho$ : 密度, $B_y$ : $y$ 方向の磁場, $u$ : $x$ 方向の速度, $\mu_0$ : 真空の透磁率, $v_A$ : Alfvén速度)
3. 方程式の離散化
3-1. FDMとは
偏微分方程式の数値解法には有限差分法 (finite difference method, FDM), 有限体積法 (finite volume method, FVM), 有限要素法 (finite element method, FEM), スペクトル法 (spectral method) 等がよく知られていますが、その中でもFDMは考え方・実装が単純でよく使われています。ただし複雑な形状は苦手なので、その場合はFVMやFEMがよく使われます (ちなみにスペクトル法は非常に高い精度を実現できる一方で、FDM以上に単純な形状しか扱えないという特徴があります)。
コンピュータは連続的なものを扱えませんので、なんらかの形で問題を離散化する必要があります。
今、時刻 $t$ は $[0, T]$, 空間 $x$ は $[0, L]$ (1次元) の範囲で扱うとして、まず時間・空間をそれぞれ $I, J$ 分割します。そして求める変数 $\mathbf{U}(t, x)$ を
\mathbf{U}(n\Delta t, j\Delta x) = \mathbf{U}^n_j \\
\Delta t = T/I, \Delta x = L/J \\
(n = 0, 1, ..., I, j = 0, 1, ..., J)
とおきます。
微分も同様に離散化する必要があります。テイラー展開を使うと
\mathbf{U}^n_{j+1} = \mathbf{U}^n_j+\frac{\partial\mathbf{U}^n_j}{\partial x}\Delta x
+\frac{1}{2}\frac{\partial^2\mathbf{U}^n_j}{\partial x^2}\Delta x^2 \\
+\frac{1}{6}\frac{\partial^3\mathbf{U}^n_j}{\partial x^3}\Delta x^3+O(\Delta x^4) \\
\mathbf{U}^n_{j-1} = \mathbf{U}^n_j-\frac{\partial\mathbf{U}^n_j}{\partial x}\Delta x
+\frac{1}{2}\frac{\partial^2\mathbf{U}^n_j}{\partial x^2}\Delta x^2 \\
-\frac{1}{6}\frac{\partial^3\mathbf{U}^n_j}{\partial x^3}\Delta x^3+O(\Delta x^4)
となるので、 $\partial\mathbf{U}^n_j /\partial x $ は例えば以下のように求めることができます。
\begin{eqnarray}
\frac{\partial\mathbf{U}^n_j}{\partial x} &=& \frac{\mathbf{U}^n_{j+1}-\mathbf{U}^n_j}{\Delta x} + O(\Delta x) \\
\frac{\partial\mathbf{U}^n_j}{\partial x} &=& \frac{\mathbf{U}^n_j-\mathbf{U}^n_{j-1}}{\Delta x} + O(\Delta x) \\
\frac{\partial\mathbf{U}^n_j}{\partial x} &=& \frac{\mathbf{U}^n_{j+1}-\mathbf{U}^n_{j-1}}{2\Delta x} + O(\Delta x^2)
\end{eqnarray}
これらの差分はそれぞれ前進差分 (forward difference), 後退差分 (backward difference), 中央差分 (central difference) と呼ばれ、それぞれ1次、1次、2次の精度であることはよく知られていると思います。
また、空間2階微分も同様にして求めることができます。こちらは2次精度です。
\frac{\partial^2\mathbf{U}^n_j}{\partial x^2} = \frac{\mathbf{U}^n_{j+1}-2\mathbf{U}^n_j+\mathbf{U}^n_{j-1}}{\Delta x^2} + O(\Delta x^2)
3-2. 安定性とCFL条件
そこで、初めの式
\frac{\partial\mathbf{U}}{\partial t}
+ \mathbf{A}\frac{\partial\mathbf{U}}{\partial x}
= \mathbf{0}
を時間は前進差分、空間は中央差分で離散化してみましょう。すると以下のようになるので、一つ後の時間ステップの値を求めることができます。
\frac{\mathbf{U}^{n+1}_j-\mathbf{U}^n_j}{\Delta t}
+ \mathbf{A}\frac{\mathbf{U}^n_{j+1}-\mathbf{U}^n_{j-1}}{2\Delta x}
= \mathbf{0}
\mathbf{U}^{n+1}_j = \mathbf{U}^n_j
-\frac{\Delta t}{2\Delta x}\mathbf{A}\left(\mathbf{U}^n_{j+1}-\mathbf{U}^n_{j-1}\right)
この差分の方法をFTCS (forward-time central-space) 法と呼びます。しかしこれを実際に計算してみると値が発散してしまいうまくいきません。
そのことを調べるために、まず方程式を2-2にしたがって変形します。
\frac{\partial W_l}{\partial t} + \lambda_l \frac{\partial W_l}{\partial x} = 0, (l = 1, 2, ..., N)
これをFTCS法で解くと、以下のようになります。
(W_l)^{n+1}_j = (W_l)^n_j
-\frac{\Delta t}{2\Delta x}\lambda_l\left((W_l)^n_{j+1}-(W_l)^n_{j-1}\right)
次に $(W_l)^n_j = V_l^n e^{ikj\Delta x}$ とおいたものを代入してみましょう。これは波数 $k$ の波を表しています。すると、
\begin{eqnarray}
V_l^{n+1} e^{ikj\Delta x} &=& V_l^n e^{ikj\Delta x}
-\frac{\Delta t}{2\Delta x}\lambda_l\left(V_l^n e^{ik(j+1)\Delta x}-V_l^n e^{ik(j-1)\Delta x}\right) \\
V_l^{n+1} &=& V_l^n
-\frac{\Delta t}{2\Delta x}\lambda_l\left(V_l^n e^{ik\Delta x}-V_l^n e^{-ik\Delta x}\right) \\
&=& V_l^n
-\frac{\Delta t}{\Delta x}\lambda_l V_l^n i\sin(k\Delta x) \\
\left|\frac{V_l^{n+1}}{V_l^n}\right|^2 &=& \left|1
-\frac{\Delta t}{\Delta x}\lambda_l i\sin(k\Delta x)\right|^2 \\
&=& 1+\lambda_l^2\left(\frac{\Delta t}{\Delta x}\right)^2\sin^2(k\Delta x) > 1
\end{eqnarray}
となることから、このスキームはどのような $\Delta t, \Delta x$ をとってきても振幅が増大していくことがわかります。
したがってFTCSスキームは無条件不安定 (unconditionally unstable) であり、この手の双曲型方程式には使うことができません。
このようにしてスキームの安定性を評価する方法をフォン・ノイマンの安定性解析 (von Neumann stability analysis) と呼びます。この手法は以下に紹介するスキームにも適用できて、例えば風上差分法で振幅が増大しない条件を求めると
\left|\lambda_l\right|\frac{\Delta t}{\Delta x} \leq 1
となります。この式の左辺をクーラン数 (Courant number) といい、このようにして求めた安定性の条件をCFL条件 (Courant-Friedrichs-Lewy Condition) と呼びます。
なお、この安定性の条件はあくまでも値が発散しない必要条件ということであって、計算精度とは別の話であることに注意してください。
4. 様々なスキーム
4-1. 風上差分法
まず簡単のため、以下の1変数の移流方程式を考えます。
\frac{\partial u}{\partial t} + a\frac{\partial u}{\partial x} = 0
これの空間差分に対し、$a$ が正の場合には後退差分、負の場合には前進差分を用いる方法を風上差分法 (upwind difference method) といいます。これは時間・空間ともに1次精度です。
具体的には以下のようになります。
\begin{eqnarray}
u^{n+1}_j &=& u^n_j
-\frac{\Delta t}{\Delta x}a\left(u^n_j-u^n_{j-1}\right) (a > 0) \\
&=& u^n_j
-\frac{\Delta t}{\Delta x}a\left(u^n_{j+1}-u^n_j\right) (a < 0)
\end{eqnarray}
常に流れの上流の方から情報を取ってくるようになっているのが風上差分と呼ばれる所以です。
これを1本の式にまとめると、以下のようになります。
u^{n+1}_j = u^n_j
-\frac{\Delta t}{\Delta x}\frac{a+|a|}{2}\left(u^n_j-u^n_{j-1}\right)
-\frac{\Delta t}{\Delta x}\frac{a-|a|}{2}\left(u^n_{j+1}-u^n_j\right)
次にこれを多変数の場合に拡張してみましょう。そこで2-2で使った対角化を再び考えます。
\frac{\partial W_l}{\partial t} + \lambda_l \frac{\partial W_l}{\partial x} = 0, (l = 1, 2, ..., N)
ここから、この $N$ 本の移流方程式それぞれについて風上差分を使えばよいことがわかります。
つまり
\begin{eqnarray}
\lambda^+_l &=& \frac{\lambda_l+|\lambda_l|}{2} &=& \max(\lambda_l, 0) \\
\lambda^-_l &=& \frac{\lambda_l-|\lambda_l|}{2} &=& \min(\lambda_l, 0)
\end{eqnarray}
とおいて、 $\mathbf{\Lambda}^+ = diag(\lambda_1^+ , \lambda_2^+, ..., \lambda_N^+),
\mathbf{\Lambda}^- = diag(\lambda_1^-, \lambda_2^-, ..., \lambda_N^-)$ を使うと、
\mathbf{W}^{n+1}_j = \mathbf{W}^n_j
-\frac{\Delta t}{\Delta x}\mathbf{\Lambda}^+\left(\mathbf{W}^n_j-\mathbf{W}^n_{j-1}\right)
-\frac{\Delta t}{\Delta x}\mathbf{\Lambda}^-\left(\mathbf{W}^n_{j+1}-\mathbf{W}^n_j\right)
となるので、 $\mathbf{A}^+ = \mathbf{K}\mathbf{\Lambda}^+\mathbf{K}^{-1},
\mathbf{A}^- = \mathbf{K}\mathbf{\Lambda}^-\mathbf{K}^{-1}$
とすれば、以下が得られます。
\mathbf{U}^{n+1}_j = \mathbf{U}^n_j
-\frac{\Delta t}{\Delta x}\mathbf{A}^+\left(\mathbf{U}^n_j-\mathbf{U}^n_{j-1}\right)
-\frac{\Delta t}{\Delta x}\mathbf{A}^-\left(\mathbf{U}^n_{j+1}-\mathbf{U}^n_j\right)
4-2. Lax-Wendroff法
まずは以下のように時間方向にテイラー展開を行います。
\mathbf{U}^{n+1}_j = \mathbf{U}^n_j+\frac{\partial\mathbf{U}^n_j}{\partial t}\Delta t
+\frac{1}{2}\frac{\partial^2\mathbf{U}^n_j}{\partial t^2}\Delta t^2+O(\Delta t^3)
次にもとの方程式
\frac{\partial\mathbf{U}}{\partial t}
+ \mathbf{A}\frac{\partial\mathbf{U}}{\partial x}
= \mathbf{0}
を時間微分します。簡単のため線形とすると、以下のように変形できます。
\begin{eqnarray}
\frac{\partial^2\mathbf{U}}{\partial t^2}
&=& -\mathbf{A}\frac{\partial}{\partial x}\left(\frac{\partial\mathbf{U}}{\partial t}\right) \\
&=& \mathbf{A}^2\frac{\partial^2\mathbf{U}}{\partial x^2}
\end{eqnarray}
したがって
\begin{eqnarray}
\mathbf{U}^{n+1}_j &=& \mathbf{U}^n_j+\frac{\partial\mathbf{U}^n_j}{\partial t}\Delta t
+\frac{1}{2}\mathbf{A}^2\frac{\partial^2\mathbf{U}^n_j}{\partial x^2}\Delta t^2+O(\Delta t^3) \\
\frac{\partial\mathbf{U}^n_j}{\partial t}
&=& \frac{\mathbf{U}^{n+1}_j-\mathbf{U}^n_j}{\Delta t} -\frac{1}{2}\mathbf{A}^2\frac{\partial^2\mathbf{U}^n_j}{\partial x^2}\Delta t+O(\Delta t^2) \\
&=& \frac{\mathbf{U}^{n+1}_j-\mathbf{U}^n_j}{\Delta t} -\frac{1}{2}\mathbf{A}^2\frac{\mathbf{U}^n_{j+1}-2\mathbf{U}^n_j+\mathbf{U}^n_{j-1}}{\Delta x^2}\Delta t +O(\Delta t, \Delta x^2)
\end{eqnarray}
となるので、もとの式の時間微分にこれを代入し、空間微分には中央差分を使うことで、以下の式が得られます。
\mathbf{U}^{n+1}_j = \mathbf{U}^n_j-\frac{\Delta t}{2\Delta x}\mathbf{A}\left(\mathbf{U}^n_{j+1}-\mathbf{U}^n_{j-1}\right) \\
+\frac{\Delta t^2}{2\Delta x^2}\mathbf{A}^2\left(\mathbf{U}^n_{j+1}-2\mathbf{U}^n_j+\mathbf{U}^n_{j-1}\right)
これをLax-Wendroff法といい、時間・空間ともに2次精度であることがわかります。
4-3. 高次の風上差分法
上の風上差分法と同様の考え方で、より高次精度のスキームを作ることもできます。
簡単のため $\mathbf{A}$ は正定値として、Lax-Wendroff法において $j+1, j, j-1$ の代わりに $j, j-1, j-2$ での値を使うようにしてみましょう。
上と同様に今度は $\mathbf{U}^n_{j-2}$ をテイラー展開すると、以下の差分が得られることを示すことができます。
\begin{eqnarray}
\frac{\partial\mathbf{U}^n_j}{\partial x} = \frac{3\mathbf{U}^n_j-4\mathbf{U}^n_{j-1}+\mathbf{U}^n_{j-2}}{2\Delta x} + O(\Delta x^2) \\
\frac{\partial^2\mathbf{U}^n_j}{\partial x^2} = \frac{\mathbf{U}^n_j-2\mathbf{U}^n_{j-1}+\mathbf{U}^n_{j-2}}{\Delta x^2} + O(\Delta x^2)
\end{eqnarray}
これを使うとLax-Wendroff法と同様にして、以下が得られます。
\mathbf{U}^{n+1}_j = \mathbf{U}^n_j-\frac{\Delta t}{2\Delta x}\mathbf{A}\left(3\mathbf{U}^n_j-4\mathbf{U}^n_{j-1}+\mathbf{U}^n_{j-2}\right) \\
+\frac{\Delta t^2}{2\Delta x^2}\mathbf{A}^2\left(\mathbf{U}^n_j-2\mathbf{U}^n_{j-1}+\mathbf{U}^n_{j-2}\right)
これはBeam-Warming法と呼ばれます。精度は時間・空間ともに2次ですが、より高次のスキームを作ることも可能です。
5. TVD性
5-1. 線形スキームの限界
さて、4で紹介したスキームを使って簡単な問題を一つ解いてみます。
1変数の線形移流方程式
\frac{\partial u}{\partial t}+a\frac{\partial u}{\partial x}=0
の解が $u(t, x) = u(0, x-at)$ となるのはよく知られていると思います。厳密解が分かっているので、この方程式を数値的に解くことで、そのスキームの精度を調べることができます。
問題は以下のように設定します。
t \in [0, T], x \in [0, L]\\
T = 4, L = 1, a = 1\\
\Delta t = 0.004, \Delta x = 0.005 \\
周期境界条件 : u(t, 0) = u(t, L)
初期条件としては、以下の2種類を考えます。
\begin{eqnarray}
ガウス関数 : u(0, x) &=& \exp\left[-\left(\frac{x-L/2}{L/9}\right)^2\right] \\
矩形波 :
u(0, x) &=& \left\{ \begin{array}{ll}
1 & (|x-L/2| \le L/10) \\
0 & (|x-L/2| \gt L/10) \\
\end{array} \right.
\end{eqnarray}
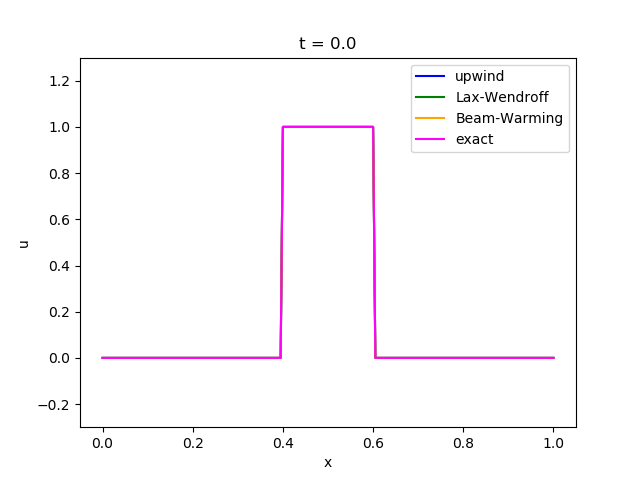
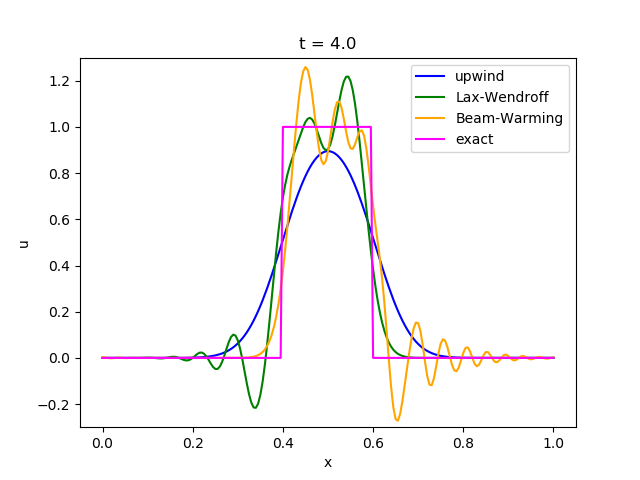
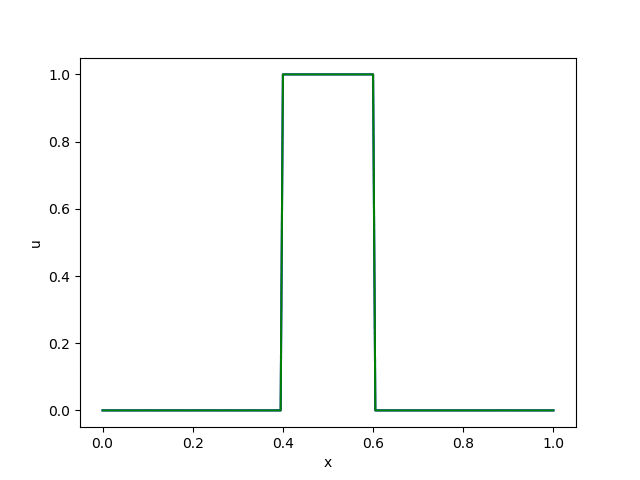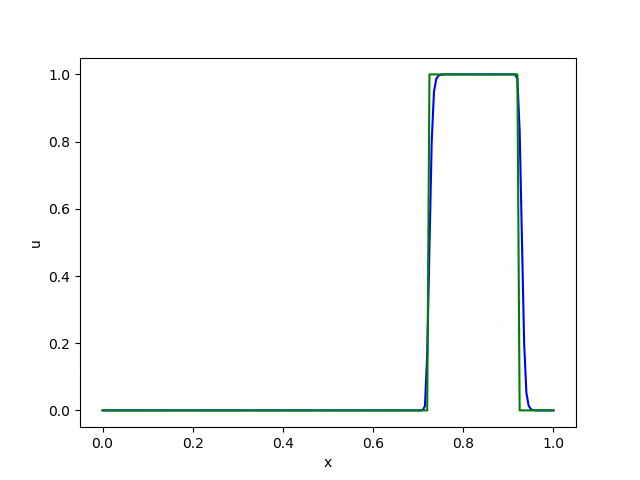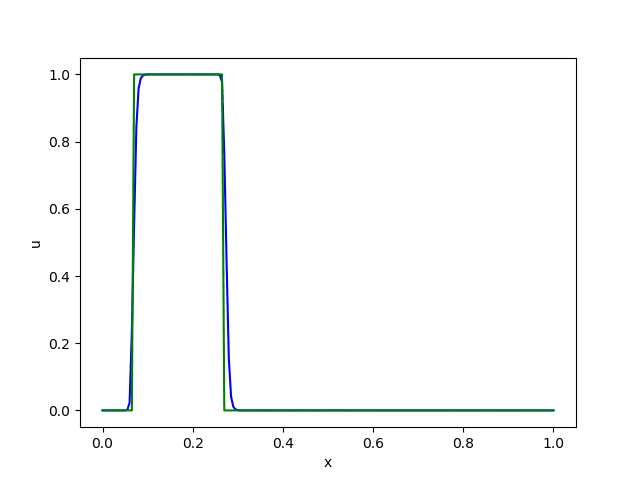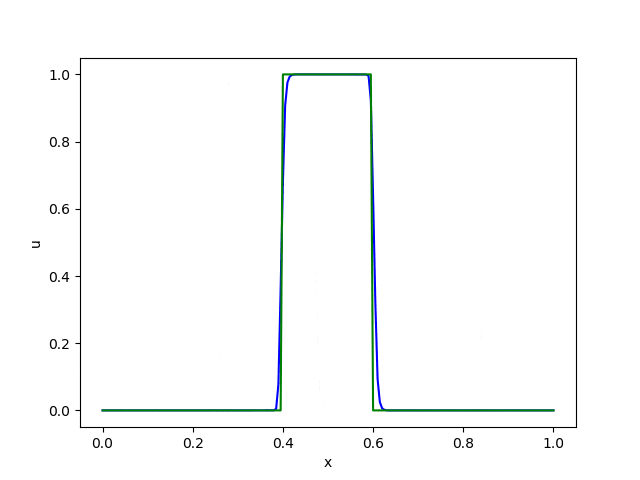
これを上で紹介した3つのスキームで計算したものが以下になります。
・ガウス関数
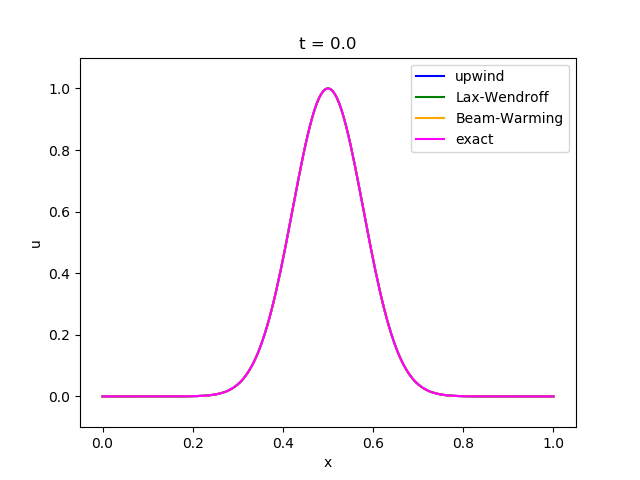
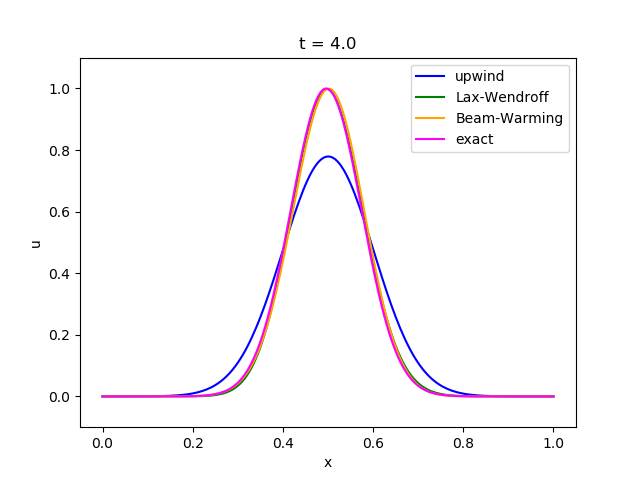
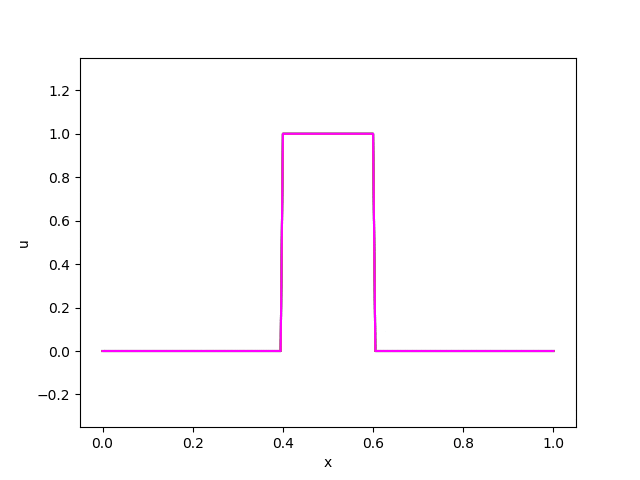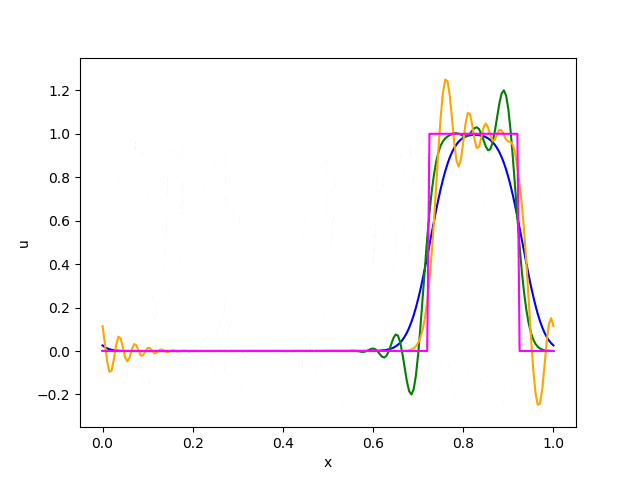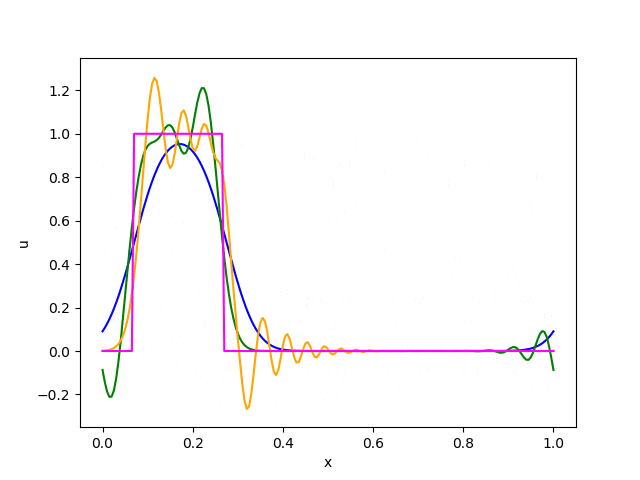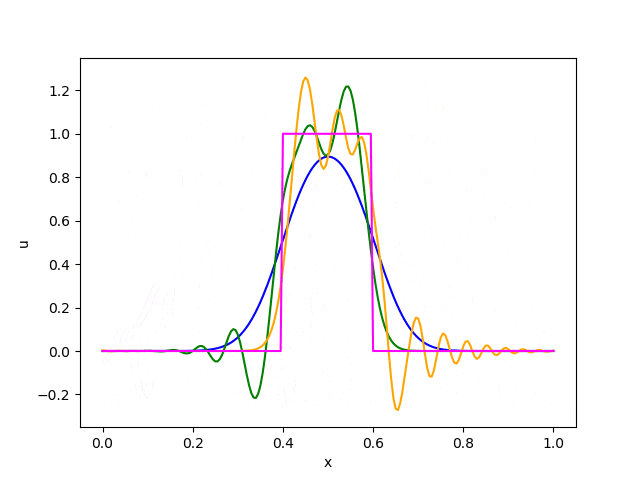
以下は動画にしたものです。(matplotlibで動画にうまくタイトルと凡例をつける方法がわかりませんでした)
・ガウス関数
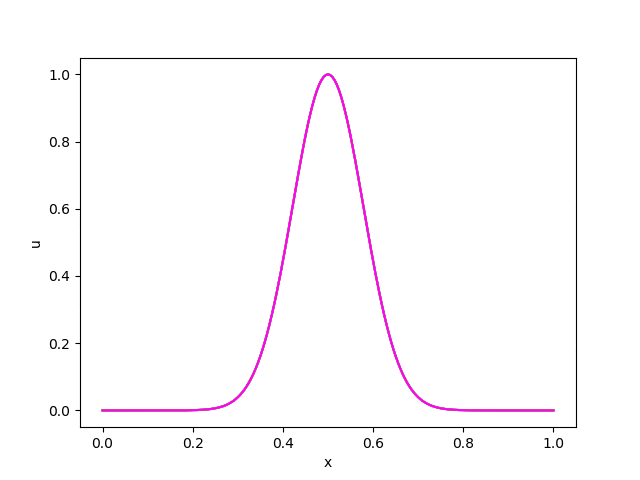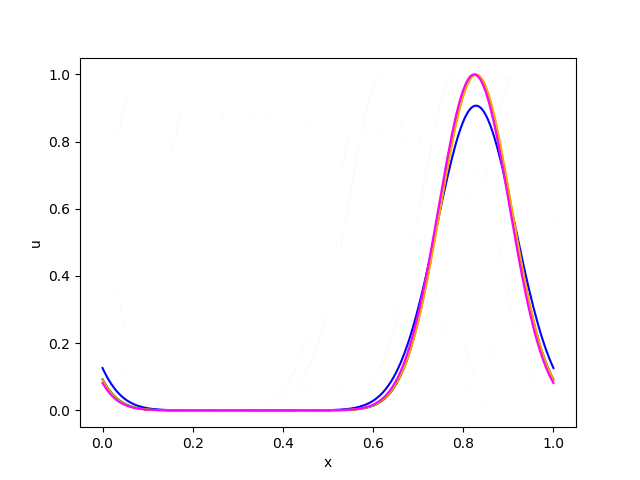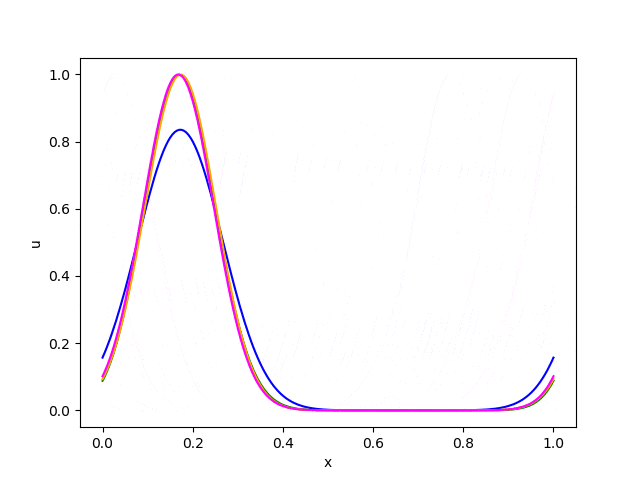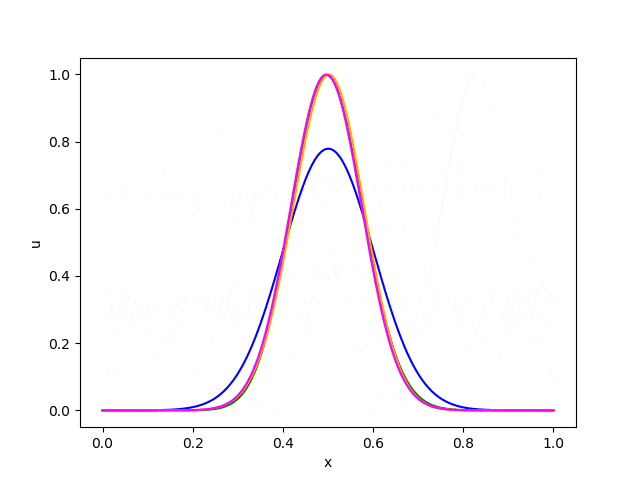
これらの結果から以下のことが読み取れます。
・風上差分法は数値拡散 (numerical diffusion) が大きく、形が次第になまってしまう。
・Lax-Wendroff法とBeam-Warming法は滑らかな関数には良好な精度を発揮するが、不連続面の近傍では数値分散 (numerical dispersion) のために余計な振動が発生する。
では、これらの欠点を克服するようなスキームはないでしょうか?
実は、このことに関して以下のGodunovの定理が成り立つことが知られています。
1変数の線形移流方程式
\frac{\partial u}{\partial t}+a\frac{\partial u}{\partial x}=0に対し、以下のような形の線形なスキームでは、2次以上の精度で解の単調性を保持できない。
u^{n+1}_j = \sum_k c_k u^n_k
解の単調性を保持するとは、 $n$ ステップ目の $u$ が単調増加/減少であるときは、 $n+1$ ステップ目の $u$ も単調増加/減少になるということです。
線形移流方程式で解は単に平行移動していくだけですから、本来なら解の単調性は保持されるべきです。逆に、これが保持されないということは余計な振動が発生することを意味しています。
これまで紹介してきたスキームはすべて線形なスキームです。したがって、これまでと同様な手法では数値拡散と数値分散の両方を同時に克服することはできません。
5-2. 流束制限関数
この不連続面は物理的には衝撃波 (shock wave) を表しています。こうした衝撃波を数値計算において精度よく捉える、いわゆる衝撃波捕獲 (shock capturing) の問題は奥が深く、これまで様々な手法が考案されてきました。
今回はその中の流束制限関数 (flux limiter) と呼ばれる手法を紹介します。
1変数の移流方程式 ($a>0$) をLax-Wendroff法で解くと、クーラン数を $C = a\Delta t/\Delta x$ とおくことで、
u^{n+1}_j = u^n_j-\frac{C}{2}\left(u^n_{j+1}-u^n_{j-1}\right)
+\frac{C^2}{2}\left(u^n_{j+1}-2u^n_j+u^n_{j-1}\right)
が得られます。
これを以下のように変形します。
u^{n+1}_j = u^n_j-C\left(u^n_j-u^n_{j-1}\right)
-\frac{C(1-C)}{2}\left[(u^n_{j+1}-u^n_j)-(u^n_j-u^n_{j-1})\right]
右辺第2項が風上差分になっていることがわかると思います。
そこで今度は以下のようにおいてみます。
\begin{eqnarray}
u^{n+1}_j &=& u^n_j-C\left(u^n_j-u^n_{j-1}\right)
-\frac{C(1-C)}{2}\left[\phi(\theta^n_{j+1/2})(u^n_{i+1}-u_j)-\phi(\theta^n_{j-1/2})(u^n_j-u^n_{j-1})\right] \\
\theta^n_{j+1/2} &=& \frac{u^n_j-u^n_{j-1}}{u^n_{j+1}-u^n_j}
\end{eqnarray}
この表記の便利なところは、ここの $\phi(\theta)$ を色々変えることで様々なスキームを表現できるところです。
例えば以下のようになります。
\begin{eqnarray}
風上差分法 : \phi(\theta) &=& 0 \\
\mathrm{Lax-Wendroff}法 : \phi(\theta) &=& 1 \\
\mathrm{Beam-Warming}法 : \phi(\theta) &=& \theta
\end{eqnarray}
今回はこの $\phi(\theta)$ を工夫することで線形スキームの欠点の克服を目指します。
さて、そのためにここでTVD (total variation diminishing) という概念を導入します。
$n$ ステップ目の $u$ に対し、全変動 (total variation) を以下のように定義します。
TV(u^n) = \sum_j \left|u^n_j-u^n_{j-1}\right|
線形移流方程式の性質を考えれば、この全変動は時間に対し増加しないと考えるのが自然でしょう。
すなわち
TV(u^{n+1}) \le TV(u^n)
この条件をTVD (total variation diminishing) といいます。
これを念頭において、先ほど導入した $\phi(\theta)$ を使った式を変形します。
\begin{eqnarray}
u^{n+1}_j &=& u^n_j-C\left(u^n_j-u^n_{j-1}\right)
-\frac{C(1-C)}{2}\left[\phi(\theta^n_{j+1/2})(u^n_{j+1}-u^n_j)-\phi(\theta^n_{j-1/2})(u^n_j-u^n_{j-1})\right] \\
\frac{u^{n+1}_j-u^n_j}{u^n_{j-1}-u^n_j} &=& C
+\frac{C(1-C)}{2}\left[\frac{\phi(\theta^n_{j+1/2})}{\theta^n_{j+1/2}}-\phi(\theta^n_{j-1/2})\right] \\
\end{eqnarray}
さて、ここでもし $u_j^{n+1}$ が $u_j^n$ と $u_{j-1}^n$ の間の値になるようにすれば、余計な振動は抑えることができます。そのとき上の式の左辺は $0$ 以上 $1$ 以下になります。
したがって、
-\frac{2}{1-C} \le \frac{\phi(\theta^n_{j+1/2})}{\theta^n_{j+1/2}}-\phi(\theta^n_{j-1/2}) \le \frac{2}{C} \\
風上差分のときのCFL条件を思い出すと、 $ 0\le C \le 1$ なので、上は
-2 \le \frac{\phi(\theta^n_{j+1/2})}{\theta^n_{j+1/2}}-\phi(\theta^n_{j-1/2}) \le 2 \\
を満たしていれば十分であることがわかります。
そこで
0 \le \phi(\theta) \le 2 かつ 0 \le \frac{\phi(\theta)}{\theta} \le 2
となる関数 $\phi(\theta)$ を与えれば、この条件を満たすことができます。
さて、これがTVDであるための条件となりますが、単にTVDであるだけなら風上差分もそうなので、せっかくならTVD性を保ちつつできるだけ2次精度になるようにしたくなります。
とすると、 $\phi(\theta)$ がLax-Wendroff法の $\phi(\theta) = 1$ とBeam-Warming法の $\phi(\theta) = \theta$ の間にくるようにするのが良さそうです。
実際、そうすることで $\theta = 1$ つまり完全に滑らかな場合はLax-Wendroff法やBeam-Warming法に一致するようにできます。
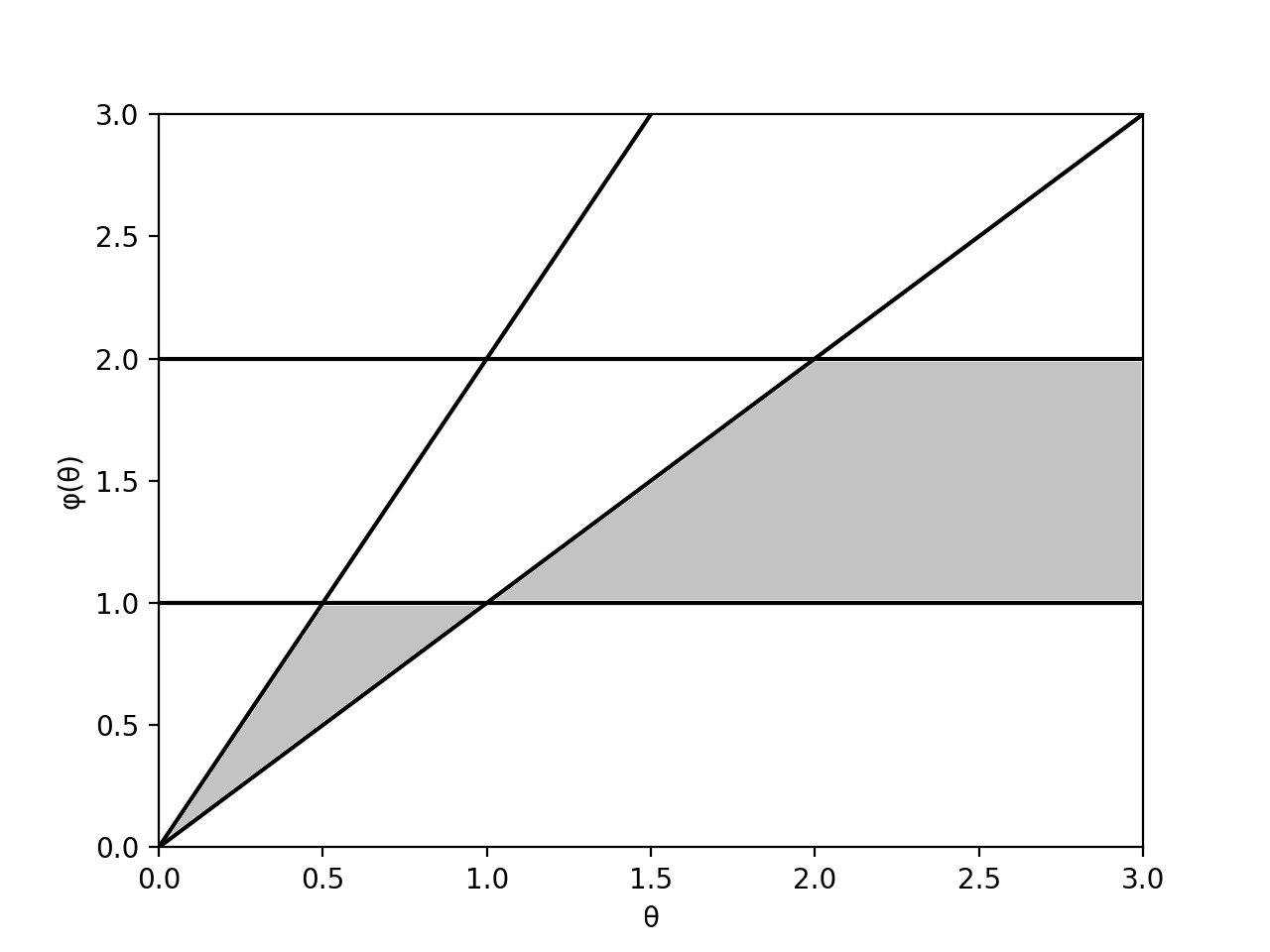
以上の条件から、下図の影をつけた部分が $\phi(\theta)$ として望ましい条件ということになります。
このようにして構成した関数を流束制限関数 (flux limiter) といい、例えば以下のようなものが考案されています。
\begin{eqnarray}
\mathrm{minmod} : \phi(\theta) &=& \max(0, \min(1, \theta)) \\
\mathrm{superbee} : \phi(\theta) &=& \max(0, \min(1, 2\theta), \min(2, \theta)) \\
\mathrm{MC} : \phi(\theta) &=& \max(0, \min((1+\theta)/2, 2, 2\theta)) \\
\mathrm{van Leer} : \phi(\theta) &=& \frac{\theta+|\theta|}{1+\theta}\\
\end{eqnarray}
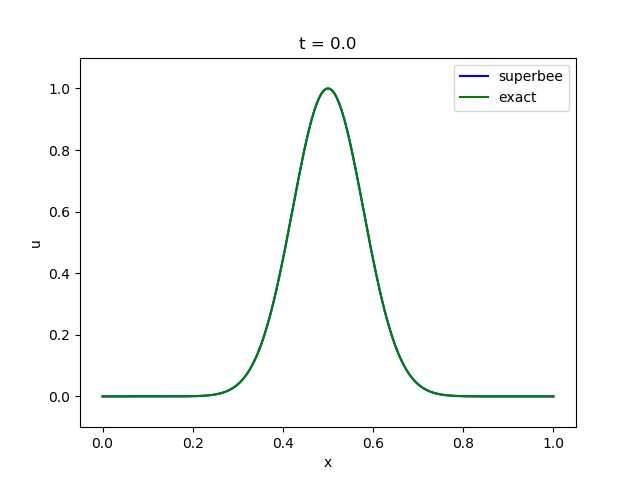
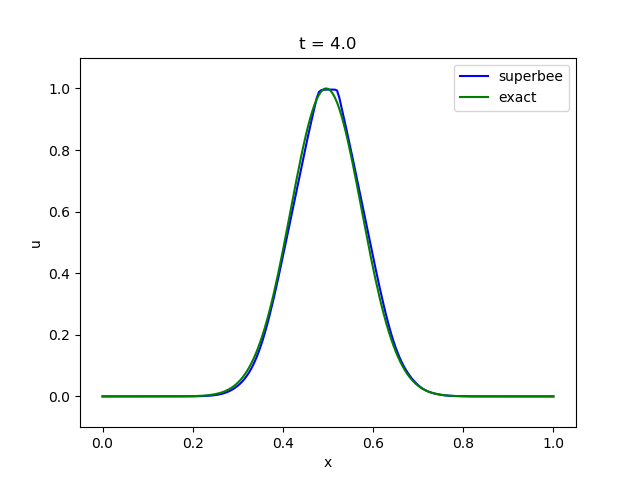
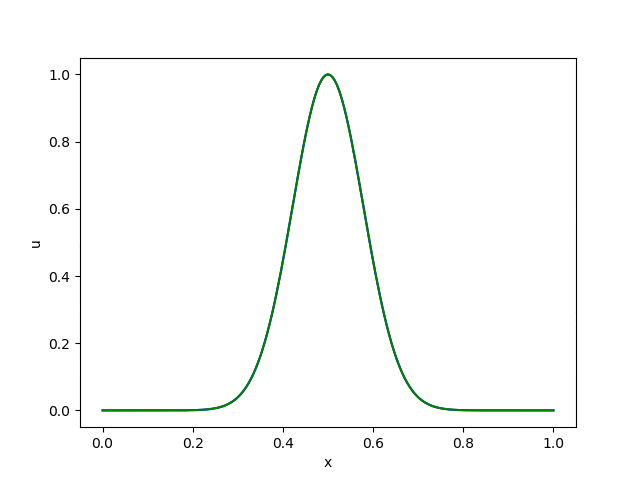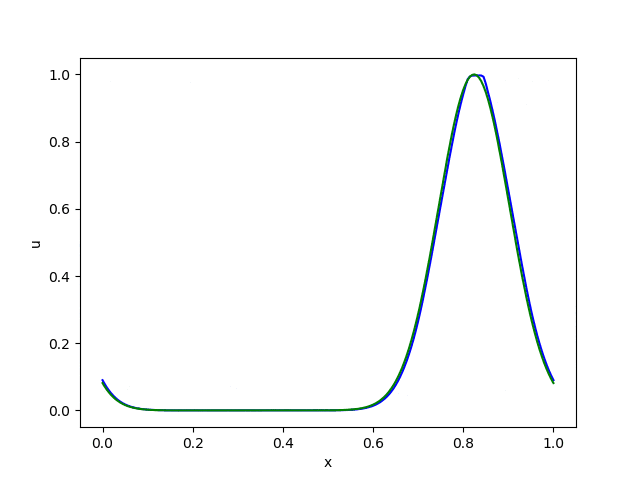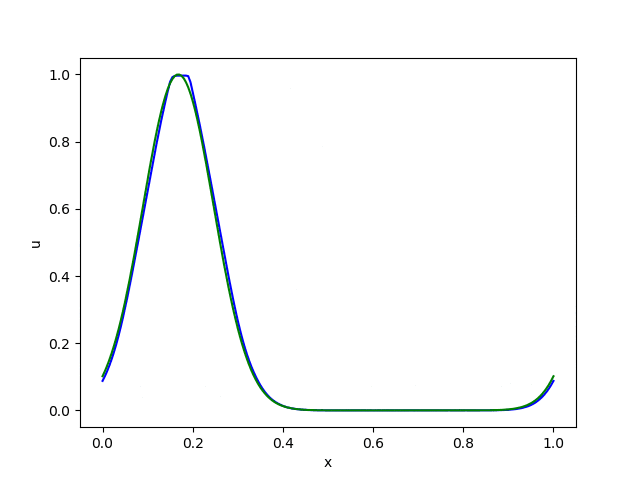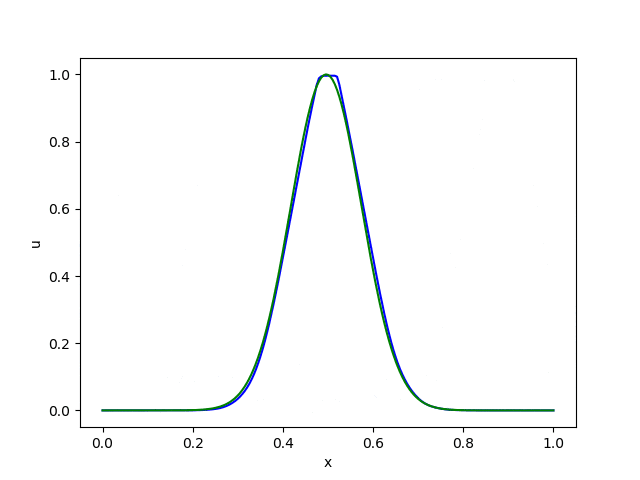
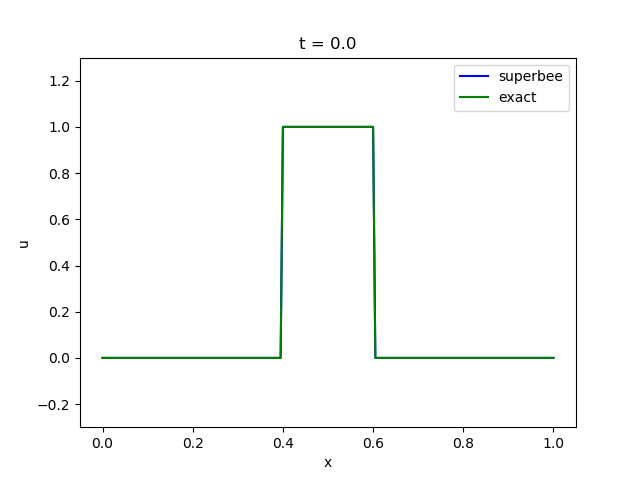
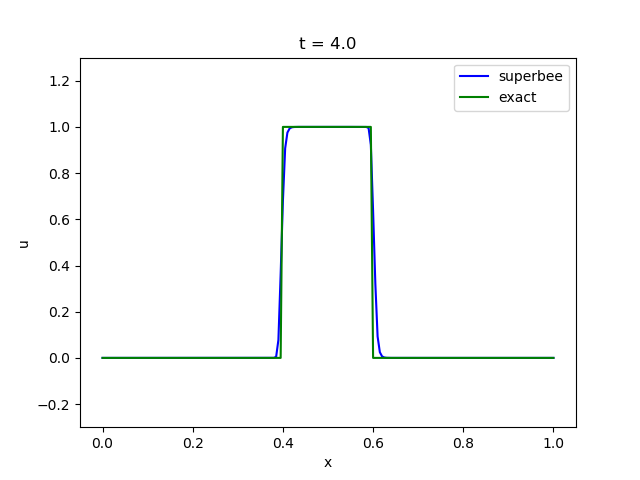
さて、ここでは試しにsuperbeeを使って先の5-1の移流方程式を解いてみましょう。
精度がかなり改善されていることがわかると思います。
6. より発展的な話題
本記事では衝撃波捕獲の方法として流束制限関数を紹介しました。他にも衝撃波に効果的に働くような人工粘性を導入したり、Riemann solver と呼ばれる、衝撃波管問題 (速度・密度・温度等の異なる2つの流体を隔てる仕切りを瞬間的に破った場合の解を求める問題) を利用した方法もあります。
後者の参考文献としては、7にも書いた
Toro, E. F. (2009), Riemann Solvers and Numerical Methods for Fluid Dynamics, Springer
がよいでしょう。
また、これらとは異なるアプローチとして、補完関数を使いながら $u$ だけでなく $\partial u/\partial x$ も同時に解くCIP法 (constrained interpolation profile method) というものも考案されています。
こちらは考案者本人による
矢部 孝, 内海 隆行, 尾形 陽一 (2003), CIP法―原子から宇宙までを解くマルチスケール解法, 森北出版
という本があります。
流体の中でも、特に宇宙プラズマや核融合プラズマの数値計算はとても難しいです。様々な方法が考案されていますがまだ発展途上といえるでしょう。興味がある人はぜひ調べてみてください。
7. 参考文献
・Toro, E. F. (2009), Riemann Solvers and Numerical Methods for Fluid Dynamics, Springer
・Leveque, R. J. (2002), Finite Volume Methods for Hyperbolic Problems, Cambridge University Press
・Versteeg, H. K. and Malalasekera, W. (2007), An Introduction to Computational Fluid Dynamics, Pearson Education Limited
・Chung, T. J. (2002), Computational Fluid Dynamics, Cambridge University Press
・Jardin, S. (2010), Computational Methods in Plasma Physics, CRC Press