MATLABでゲーム作成：マインスイーパを何行でかけるかを挑戦してみた

MATLABでゲーム作成

MATLABでプログラムコードを簡単に少数行で書けるとイメージが強いですが、今回ははその背景もあり、さあ、マインスイーパゲームを何行で書けるかを試してみた。
もちろん、ここで紹介する例が最も数少ない行で書けたマインスイーパとは保証しない。
また、今回はタイミングの計測を省略している。
※マインスイーパはどんなゲームなのかを分かる一例：　
http://www.freeminesweeper.org/minecore.html

環境

MATLABのR2019aバージョン
Windows10
MATLAB Toolbox: Image Processing Toolbox

MATLABのハンドルグラフィックス

MATLABで描画のため提供されるハンドルグラフィックスを使って色々なゲームを簡単に書ける。
今回は、MATLABのFigure (figure関数)、Panel（uipanel関数）とボタン（uicontrol関数）のみを使って試している。

全体のフロー

プログラム作成のフロー：
１．画面を作成
２．データ設定：マインがあるマス、各種マス（正方形のボタン）に表示するマイン数の計算
３．各種マスをクリックした時、稼働するプログラム（コールバック関数）を作成

ステップ１：画面作成

まずは、ハンドルグラフィックスの各種関数を使って画面を作成する。今回の例では、例えば、１５×１５のマス行列に２０個のマインを設定してみる。各マスの辺の長さを３０ピクセルとする。

ステップ２：データ設定

乱数によって１５×１５のマス行列の適当な２０ヶ所の位置にマインを設定する。
その後、それぞれのマスの３×３近傍に何個のマインがあるかを計算する。

※行数を減らすため、ステップ１とステップ２を合わせてコードを書いている。
その理由は、各種マスのためボタンを設定するとき、それぞれのボタンに表示すべく数値（上記３×３近傍に何個のマインがあるか）を埋め込むため。

%ここまではFigureとPanelを作成
hF      = figure('Position',[50 100 1.2*15*(30+1) 1.2*15*(30+1)],'numbertitle','off','Name',['(',num2str(20),')']);%最初はFigureを作ります
pnlL    = [15*(30+1)+3 15*(30+1)+2];%Figureに付けるパネルの長さ計算
pnlS    = [(hF.Position(3) - pnlL(1))/2 (hF.Position(4) - pnlL(2))/2];%Figureにつけるパネルの幅を計算
pnl     = uipanel(hF,'Units','Pixel','Position',[pnlS pnlL],'title','');%パネル作成

%ここからは先にステップ２のデータ設定を実施
mVal    = calculateMineNumber_Min(15,randperm(15^2,20));%乱数によってマイン生成⇒グリッドごとに周辺のマイン数を計算する関数

%ここで各種マスに対応するボタンを定義
[PX,PY] = meshgrid(1:(30+1):15*(30+1),1:(30+1):15*(30+1));%それぞれのグリッドの位置を一気に計算
bHndl   = repmat(uicontrol(pnl),[15,15]);%グリッド作成用、各グリッドのハンドルを初期化
for k   = 1 : 15^2 %Loopで「15×15」のグリッドを作成
    bHndl(k) = uicontrol(pnl,'Position',[PX(k),PY(k),30,30],'UserData',mVal(k),'String',mVal(k),'ForegroundColor',[0.9 0.9 0.9],'BackgroundColor',[0.9 0.9 0.9]);%グリッド作成
end

%それぞれのボタンにコールバック関数の適用
st      = regionprops(mVal<= 0,'PixelList','PixelIdxList');%計算に使うため周辺にマインがないグリッドのインデックスを抽出し周辺にマインがないグリッドの塊を作成
set(bHndl,'Callback',{@coreFcn_M,15,mVal<= 0,st,bHndl});%それぞれのグリッドをクリックしたら稼働するコールバック関数を適用

コメントのみの行を除外すると、意外と少量のコード（たった１２行）になる。
ただし、乱数によってマイン生成し、グリッドごとに周辺のマイン数を計算する関数として「calculateMineNumber_Min.m」という別ファイル使用しているが、こちらは以下のようになる（３行）。

mVal        = zeros(Gridsize,Gridsize);%初期化
mVal(mnPs)  = Gridsize^2+1;%乱数で生成した位置にマインがあることを指定（大きな数値を挿入）
mVal        = mVal+(mVal<=0).*imfilter(mVal,ones(3,3))/(Gridsize^2+1);%マス３×３近傍のマイン数計算

ステップ３：コールバック関数を作成

マインが入っているマスが押されると、「Game Over」になる。
周辺３×３近傍が０であるマスが押されると、そのマスにリレー接続されている周辺３×３近傍が０であるすべてのマスが公開される。ここでは、画処理によく使われる形態学的処理を用いて、MATLABのビルトイン関数をそのまま使い、行数をぐ～んと減らす。
周辺３×３近傍が数値（１～８）であるマスが押されると、そのマスのみが公開される。
また、ゲームクリア―されたら、つまり、すべてのブロックが公開されたら「Congratulations」を表示する。

function coreFcn_M(hndl,~,Gridsize,bI,st,bHndl)
if hndl.UserData > Gridsize^2    %If hits Mine
    set(hndl,'BackgroundColor',[1 0 0],'ForegroundColor',[0 0 0],'String','●');
    errordlg('Game Over!','!!!');
    set(bHndl,'Callback','');
elseif hndl.UserData == 0       %If hits a block without number (Should expand to all connected blocks without number)
    hInd    = find(bHndl==hndl);    %Find blob containing current button
    for k = 1 : numel(st)
        if ~any(st(k).PixelIdxList == hInd)
            bI(st(k).PixelIdxList) = false; %only keep the current button blob alive
        end
    end
    bI = bwmorph(bI,'thick',1); %Expand one pixel to border for current button blob
    UD = [bHndl.UserData]';
    set( bHndl(bI(:)&UD<=Gridsize^2),'Style','Edit','Enable','inactive','ForegroundColor',[0 0 0],'BackgroundColor',[1 1 1]);
    set( bHndl(bI(:)&UD<=Gridsize^2&UD<=0),'String','')
else %If hits a block with number
    set(hndl,'Style','Edit','Enable','inactive','ForegroundColor',[0 0 0],'BackgroundColor',[1 1 1]);
end
%Win check
if sum(~strcmpi({bHndl.Style},'edit'))==sum([bHndl.UserData]>Gridsize^2)
    msgbox('Congratulations!!','WIN')
end

このコールバック関数も２１行で完成できた。
合計、３３行でマインスイパーを作ってしまえる。少し感動してもいいかな～と。
勿論、ハンドルグラフィックスのスクリプトの部分を下記のように関数化すると、ほぼ同様な行数のプログラムでマスの個数やマインの個数を変数にしていろいろなサイズのマインスイパーを楽しめることができる。

function createGame_Minimum(mnum,grsz,esz)
hF      = figure('Position',[50 100 1.2*grsz*(esz+1) 1.2*grsz*(esz+1)],'numbertitle','off','Name',['(',num2str(mnum),')']);%最初はFigureを作ります
pnlL    = [grsz*(esz+1)+3 grsz*(esz+1)+2];%Figureに付けるパネルの長さ計算
pnlS    = [(hF.Position(3) - pnlL(1))/2 (hF.Position(4) - pnlL(2))/2];%Figureにつけるパネルの幅を計算
pnl     = uipanel(hF,'Units','Pixel','Position',[pnlS pnlL],'title','');%パネル作成
mVal    = calculateMineNumber_Min(grsz,randperm(grsz^2,mnum));%乱数によってマイン生成⇒グリッドごとに周辺のマイン数を計算する関数
[PX,PY] = meshgrid(1:(esz+1):grsz*(esz+1),1:(esz+1):grsz*(esz+1));%それぞれのグリッドの位置を一気に計算
bHndl   = repmat(uicontrol(pnl),[grsz,grsz]);%グリッド作成用、各グリッドのハンドルを初期化
for k   = 1 : grsz^2 %Loopで「grsz×grsz」のグリッドを作成
    bHndl(k) = uicontrol(pnl,'Position',[PX(k),PY(k),esz,esz],'UserData',mVal(k),'String',mVal(k),'ForegroundColor',[0.9 0.9 0.9],'BackgroundColor',[0.9 0.9 0.9]);%グリッド作成
end
st      = regionprops(mVal<= 0,'PixelList','PixelIdxList');%計算に使うため周辺にマインがないグリッドのインデックスを抽出し、周辺にマインがないグリッドの塊を作成
set(bHndl,'Callback',{@coreFcn_M,grsz,mVal<= 0,st,bHndl});%それぞれのグリッドをクリックしたら稼働するコールバック関数を適用

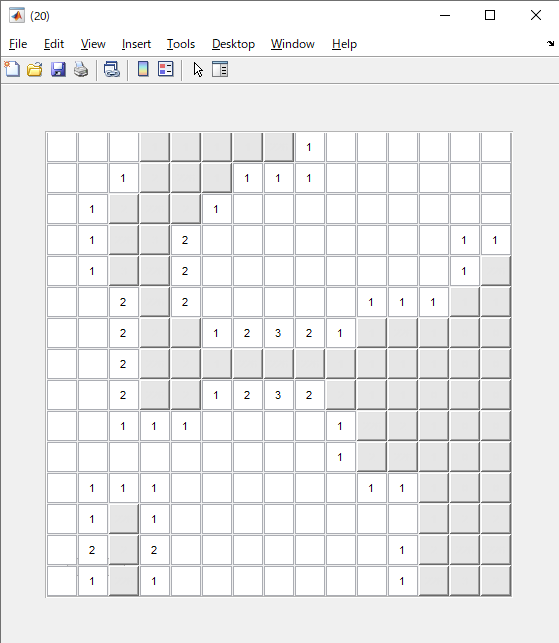
作成物の紹介

プログラムを実行してみた。

>> createGame_Minimum(20,15,30)

このようなイメージ:

おわりに

今回は３３行でマインスイーパゲームの作成ができた。
元々、マインの個数計算や近傍周辺にマインがないマスを一気に開くため、MATLABのImage Processing Toolboxのビルトイン関数が有効だと気付いた時に「少量コードで書けちゃうぞ～」とおもっていたが、それにしても、やってみたら、たったの３３行で完成できたことには、正直、少し驚いた。
やはり、MATLABの便利な関数を利用するポイントが非常に大きかった。

もっと、少ない行数で作られることができれば、是非、コメントいただきたい。
また、読まれて楽しかったら、「いいね」をお忘れずに。