頂点シェーダで曲面を作る

やりたいこと

画像を任意の曲率で円柱型に曲げたときの画像を作る必要がありました。

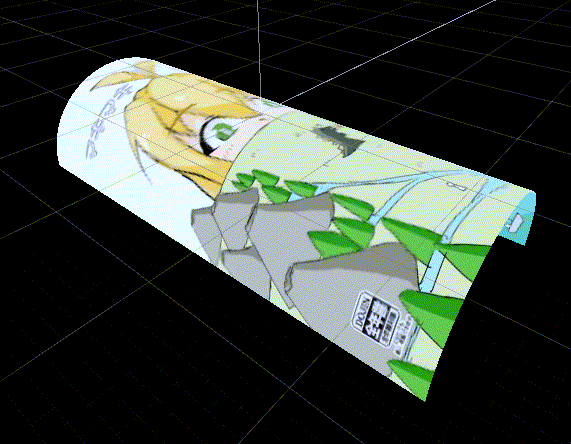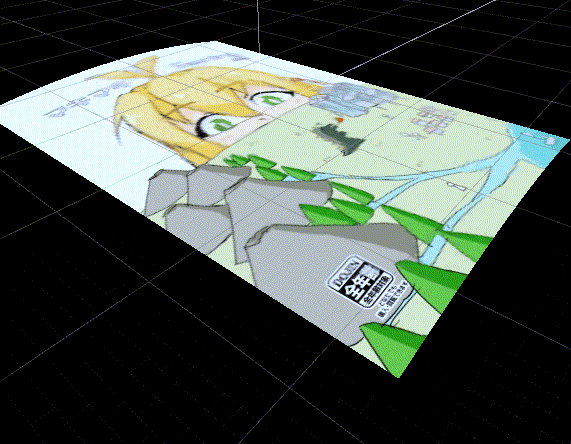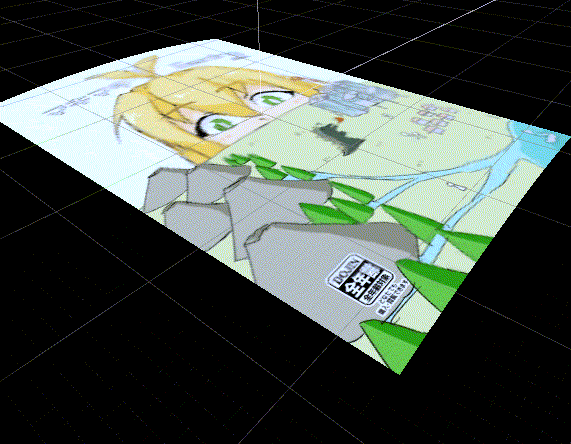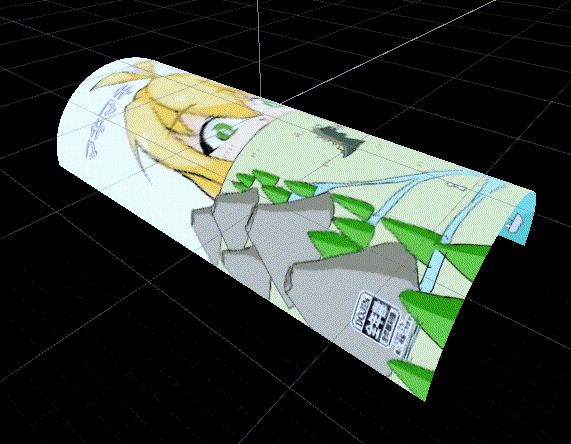
GIFでは曲率半径を1~3unitに変動させています。

幾何的な話

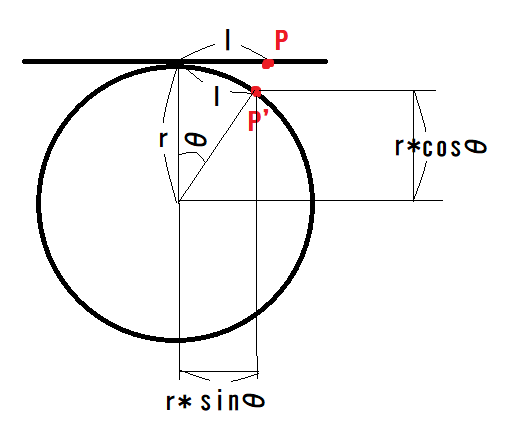
点Pの座標とrが分かっていて、P'の座標を求めたい訳です。円の全周が2πr（2π）でそのうちのθだけなので、l=rθです。これでθが求まりました。あとはxはcos、yはsinで座標が求まります。

実装

C#で頂点バッファをいじってもいいのですが、シェーダでいじった方が手っ取り早そうなので今回はSurfaceShaderで書きます。モデルの方は適度に細かい網目状の長方形を用意しておきます。（横幅を1unitに）

C#から曲率半径を受け取るために、_Radiusを宣言します

Properties
{
    _MainTex ("Albedo (RGB)", 2D) = "white" {}
    _Radius ("Radius", Range(1, 20)) = 1.0
}

頂点シェーダを明示します。

#pragma surface surf Lambert vertex:vert

頂点シェーダ本体です。簡便にするため、横幅1unitだったモデルをπunitに引き伸ばしてから処理しています。

void vert(inout appdata_full v, out Input o )
{
    UNITY_INITIALIZE_OUTPUT(Input, o);
    float pi = 3.1415926;
    float l = v.vertex.z * pi / 2;
    float r = _Radius;
    float th = l/r;
    v.vertex.xyz = float3(v.vertex.x *pi/2, r*cos(th)-r, r*sin(th));
}

コード全体

arch.shader

Shader "Custom/arch"
{
    Properties
    {
        _MainTex ("Albedo (RGB)", 2D) = "white" {}
        _Radius ("Radius", Range(1, 20)) = 1.0
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100
        Cull off

        CGPROGRAM
        #pragma surface surf Lambert vertex:vert
        #pragma target 3.0

        sampler2D _MainTex;
        float _Radius;
        struct Input
        {
            float2 uv_MainTex;
        };

        void vert(inout appdata_full v, out Input o )
        {
            UNITY_INITIALIZE_OUTPUT(Input, o);
            float pi = 3.1415926;
            float l = v.vertex.z * pi / 2;
            float r = _Radius;
            float th = l/r;
            v.vertex.xyz = float3(v.vertex.x *pi/2, r*cos(th)-r, r*sin(th));
        }

        void surf (Input IN, inout SurfaceOutput o) {
            fixed4 c = tex2D (_MainTex, IN.uv_MainTex);
            o.Albedo = c.rgb;
            o.Alpha = c.a;
        }
        ENDCG
    }
    FallBack "Diffuse"
}