目次
- はじめに
- DAC is 何
- サンプリングについて
- 符号化について
- オーバーサンプリング
- アップコンバージョン
- アンダーサンプリング
- 帯域幅について
- フィルタ
- アナログフィルタ
- LCフィルタ
- CRフィルタ
- RLCフィルタ
- デジタルフィルタ
- IIRフィルタ
- FIRフィルタ
- CICフィルタ
- デジタルフィルタの例
- ローパスフィルタ(LPF)
- ハイパスフィルタ(HPF)
- バンドパスフィルタ(BPF)
- バンドエリミネーションフィルタ(BEF)
- デシメーションフィルタ
- インターポレーションフィルタ
- アナログフィルタ
- おわりに
はじめに
DACの使い方全然わからん。。。
フィルタって何よ。。。
となったので、DACとフィルタについて調べてまとめてみました。
また、対となる記事「ADCの分解能計算とサンプリングについて考えてみた」に図を追加しました。
DAC is 何
Digital to Analog Converter 略して、DAC。1
デジタルの電気信号をアナログの電気信号に変換してくれる回路のことを指します。
修正_2024/12/21
DACの信号の出しにはオペアンプがいまして、バッファとして使用されます。
DACは端子に複数bitを出力することで、電流量を調整し、オペアンプの信号出力を細かく制御します。
この「オペアンプを使って複数bitを特定の電圧のアナログ信号に変換を行う回路」のことを、一般にDACと呼んでいるわけです。
デジタル信号はアナログ回路に直接入力してもパルス信号としか認識されないため、量子化された信号をDACを用いてアナログ信号に変換してから出力します。
モータの制御信号や音の信号、無線信号なんかはアナログ信号ですから、DACを使ってアナログ信号に変換してやることで、ソフトウェアからの制御が可能となるわけですね。
追記_2024/12/21
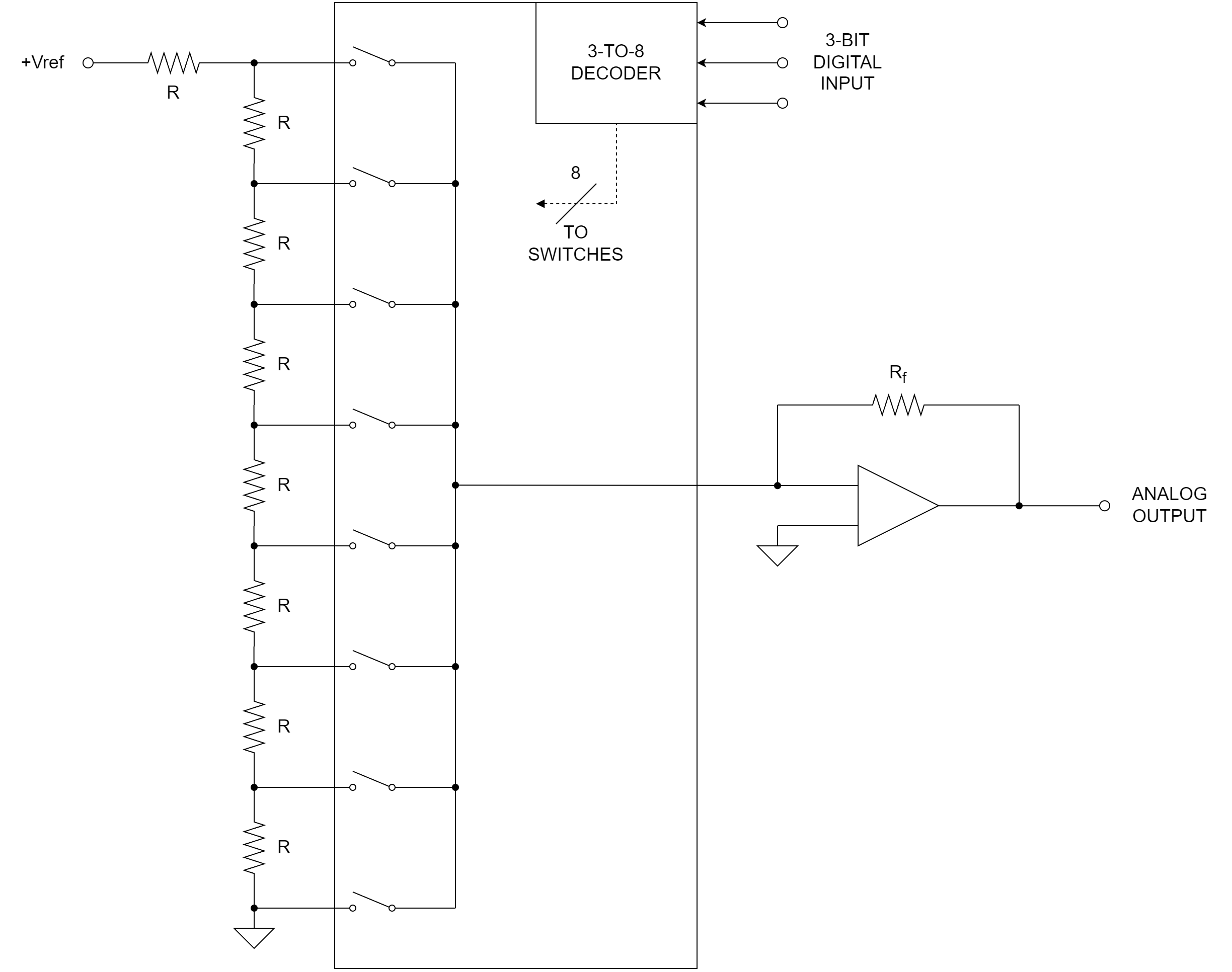
以下にDACの一例を示します。
参考図の資料は、以下になります。
サンプリングについて
ここではサンプリング定理のおさらいや追加の解説をしつつ、DAC向けのサンプリング定理の説明を行います。
ここ↓ で解説した通り、ADCにおけるサンプリング定理はサンプリング周波数の半分であるナイキスト周波数が重要で、復元後の信号の周波数がナイキスト周波数の範囲内となるように設定 します。
ADCの分解能計算とサンプリングについて考えてみた
これに対して、DACは復元前のデジタル信号の持つ情報がサンプリング定理を満たしている 必要があります。
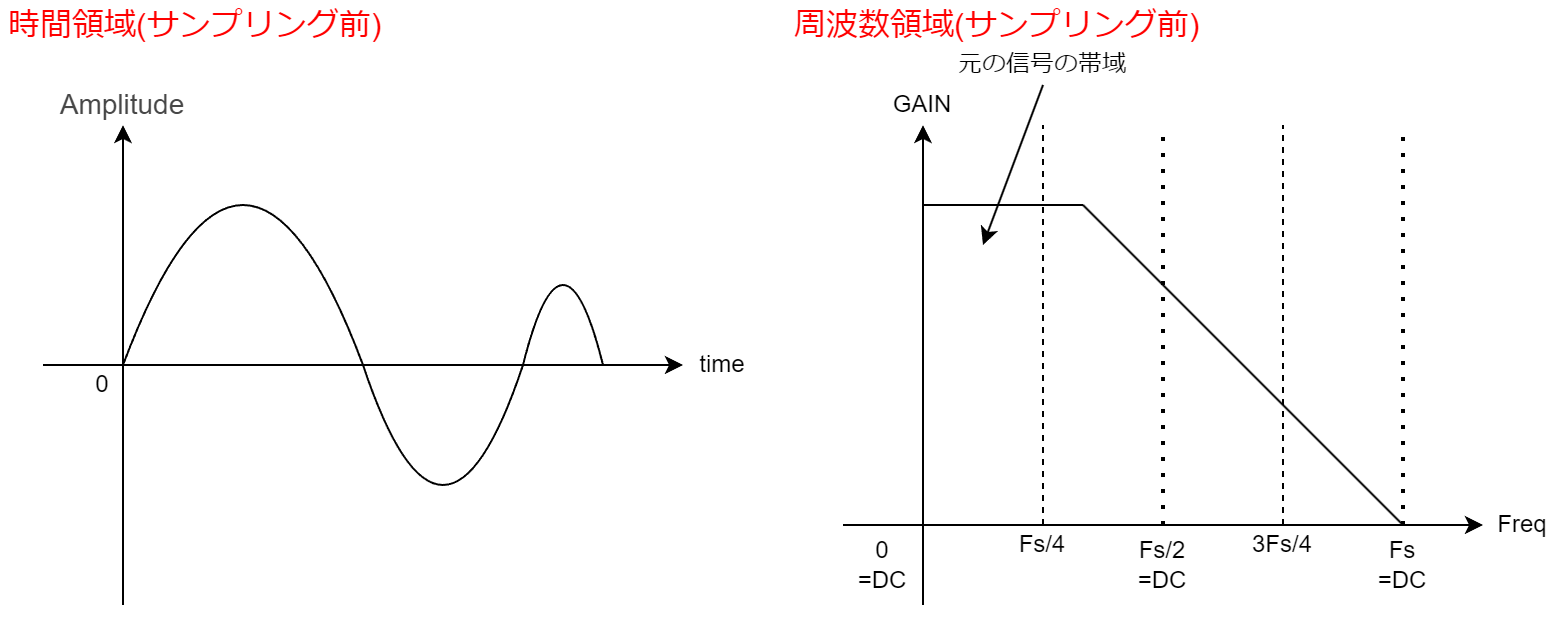
アナログ信号というのは、以下に示す通り周波数領域で限定された信号となっています。
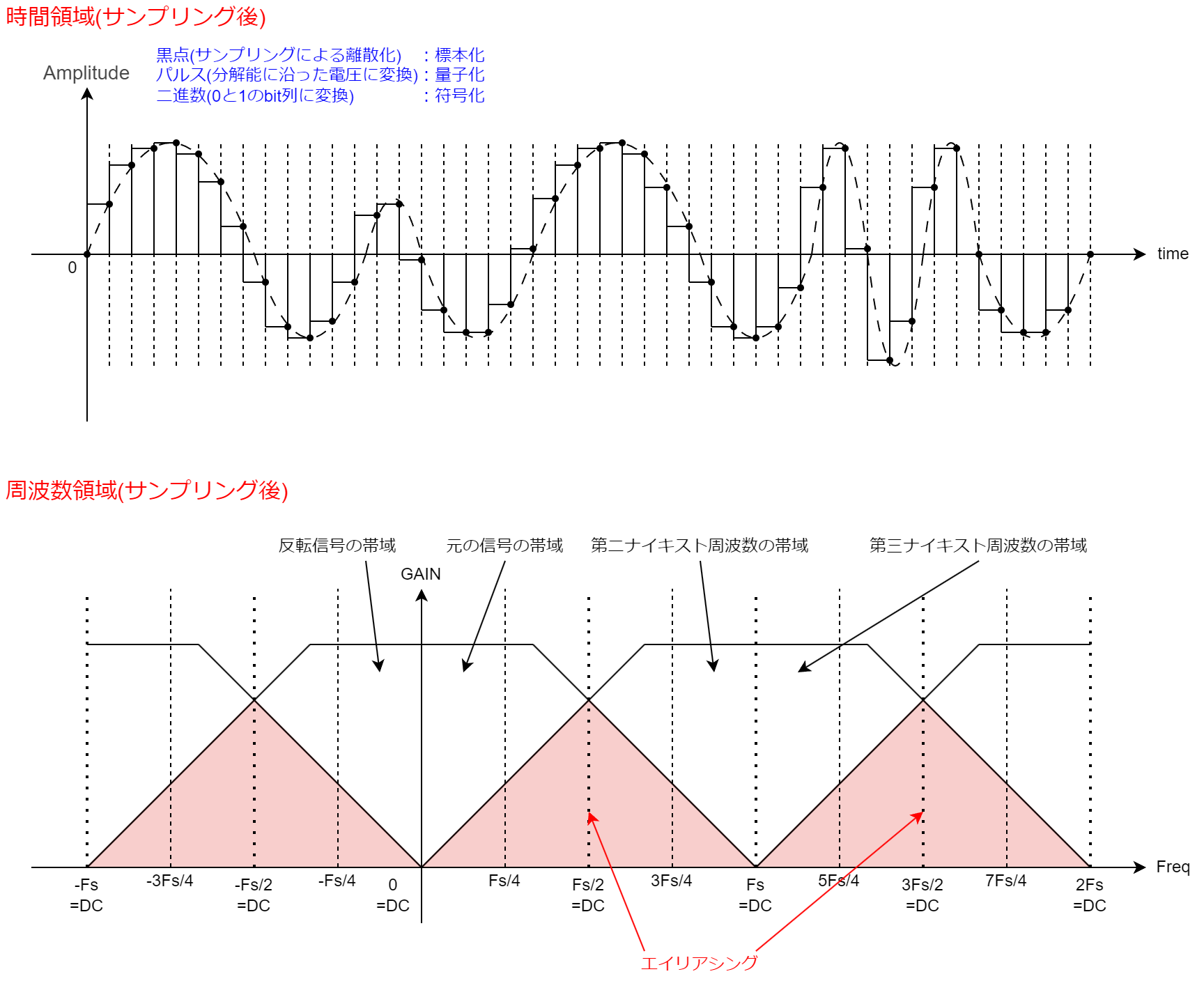
これに対してADCによってデジタル信号に変換された信号やアナログ信号に変換可能なバイナリデータの列は、以下に示す通り周波数領域で無限に値を取ります。
デジタル信号に変換した信号が周波数領域で無限に値を取るのは、「離散時間フーリエ変換の効果によって、アナログ信号がデジタル信号に変換される際に標本化(離散化)されて、高調波側に信号が複製されたこと」と同等であるためです。
この複製された信号のことを一般的に 「イメージ信号」 と呼びます。
また、複製されたイメージ信号を 「折り返し雑音」(エイリアス) とも言います。
「折り返し雑音」(エイリアス) と重なって元の信号が復元できなくなる現象を、
エイリアシング と言います。
イメージ信号は、デジタル信号の中で元の信号と区別されないため、工夫してやることで元の信号と異なる周波数の信号を選択的に取り出すことが可能となります。 なので、ADCを用いなくてもPC上で作成したバイナリデータとDACさえあれば、必要なアナログ信号の出力が可能なわけですね。
ただし、エイリアシングが発生してしまうと、隣のイメージ信号と混ざってしまうため、元の信号が復元できなくなってしまうわけです。
「…あれ？ADCでサンプリングしたり、バイナリデータから生成したデジタル信号を出力したりすると、周波数領域に周期的な信号が生成されることと同等になるのであれば、DACのアナログ信号出力にも高調波成分が出力されておかしくなるんじゃないの？」
と考えた方。あなたは正しい。ここ↓ にちゃんと書いてあります。普通に考えれば、離散値からの復元時にイメージ信号まで復元されてしまい、元の信号が復元できません。
やる夫で学ぶディジタル信号処理_5. 離散時間フーリエ変換
ではどうするのが良いかというと、ここ↓ に書かれています。
やる夫で学ぶディジタル信号処理_10. サンプリング定理
上記サイトには、 「通常の離散時間フーリエ変換の考え方のままだと、離散時間フーリエ逆変換では周波数領域で周期的(連続的)な関数を扱うことになるから、離散値しか取れないコンピュータでは離散時間フーリエ逆変換を扱えない」 と記載されています。
その矛盾を解消するために、離散時間フーリエ逆変換の代わりに 逆フーリエ変換(離散時間フーリエ逆変換ではない)とくし型関数を組み合わせたもの を扱うことで、実用的なサンプリング定理がまとめられています。
離散的で周期的 なくし型関数を用いているので、元の信号を 「周波数領域では連続的で非周期的な関数、時間領域では連続的で非周期的な関数」 として扱うことができます。234
上記内容を踏まえた上で、DACにあてはめますと、「DAC出力は sinc関数(周波数領域に矩形窓の関数) のフィルタがかかった出力となり、周波数領域に帯域制限がかかるため、出力信号が連続的な関数となる。」 となります。
つまり、ADCでサンプリングしたイメージ信号だらけのデジタル信号をDACで出力しても、DACの構造上、出力にsinc関数がかかった状態となるため、元の信号が復元可能というわけですね。
これは、サンプリングを行ってデジタル信号に変換した信号を元のアナログ信号に戻しても、サンプリングによって発生したイメージ信号の折り返し雑音による高調波ノイズをあまり気にすることなく復元できる ということです。
このようなDAC出力にsinc関数のフィルタがかかる現象を 「アパーチャ効果」 といいます。
これにより、DACのデジタル側で特に処理することなく、ナイキスト周波数を守ったアナログ信号の取得が可能となります。
DACはイメージ信号を含むいずれかの信号の中からsinc関数によって周波数を選択して、逆フーリエ変換によってアナログ信号に戻してやるので、エイリアシングが発生しないように帯域を制限する仕組みが必要となります。その帯域制限の仕組みの一つがサンプリング定理なわけですね。
DAC出力時のsinc関数の基準周波数は、DA変換前のサンプリング周波数に依存するため、サンプリングデータのサンプリングレートを高くすることによって、出力する信号の周波数を高くすること(アップコンバージョン) ができます。
符号化について
前回のADCの記事では、標本化と量子化について触れましたが、符号化については触れていなかったので、ここに記載します。
ここ↓ のRohmのページを見ると、ADCを使ったサンプリングは 標本化 → 量子化 → 符号化 と進んでアナログ信号がデジタル信号に変換されるようです。
標本化はアナログ信号を離散的な値に変換する処理で、量子化は標本化した信号を近似する処理、符号化は近似した値をデジタル値にあてはめる処理ですね。
つまりADCは 標本化 → 量子化 → 符号化 と処理が進むのに対して、DACはADCの逆操作で、符号化 → 量子化 → 標本化 の操作となりますね。
オーバーサンプリング
ADCではサンプリング時の量子化誤差が小さくなるという話をしました。
DACも同じでアナログ信号への変換時に量子化誤差が小さくなります。
なので極力サンプリング周波数の高いDACを使うことが、ノイズ削減の近道となり、DACもADCと同じくサンプリング定理を守って扱う必要があります。
(量子化誤差が高調波となっていくため、LPFの設計がやりやすくなる)
アップコンバージョン
オーバーサンプリングとは違い、復元する信号の周波数をアップコンバートすることを「アップコンバージョン」と言います。
考え方は「サンプリングの点を増やす」という点においてオーバーサンプリングと同じですが、復元される信号の周波数はオーバーサンプリングと異なります。
アップコンバージョンすることで、基本周波数の整数倍の信号を生成すること が可能です。
アンダーサンプリング
アンダーサンプリングは、ADCで信号をサンプリングすることによってアナログ信号の周波数をダウンコンバート5することが肝の技術です。
したがって、DACではアンダーサンプリングを使用できません。
ADCはその構造上、2024年現在の技術では 2.048GSPS までしか出せません。4.096GSPS以上のサンプリング周波数で動作可能なADCはすべて、2.048GSPSのサンプリング周波数で動作可能なADCを並列動作させています。
なので、ADCは高い周波数のサンプリングにアンダーサンプリングの技術を使うわけですね。
対してDACはその構造上、ADCより高いサンプリング周波数で動作可能であるため、デジタル側で変換したうえで出力すれば良いわけですね。
帯域幅について
信号の周波数を考える際に、信号周波数の範囲を考えることがあります。正弦波だと周波数領域に1本のピークが立つだけですが、正弦波を組み合わせた信号を出力すると周波数領域に幅を持った形で現れることがあります。
このときの周波数の幅を 「帯域幅」 と言います。
帯域幅について、以前の記事のアンダーサンプリングの項で出した例を元に解説します。
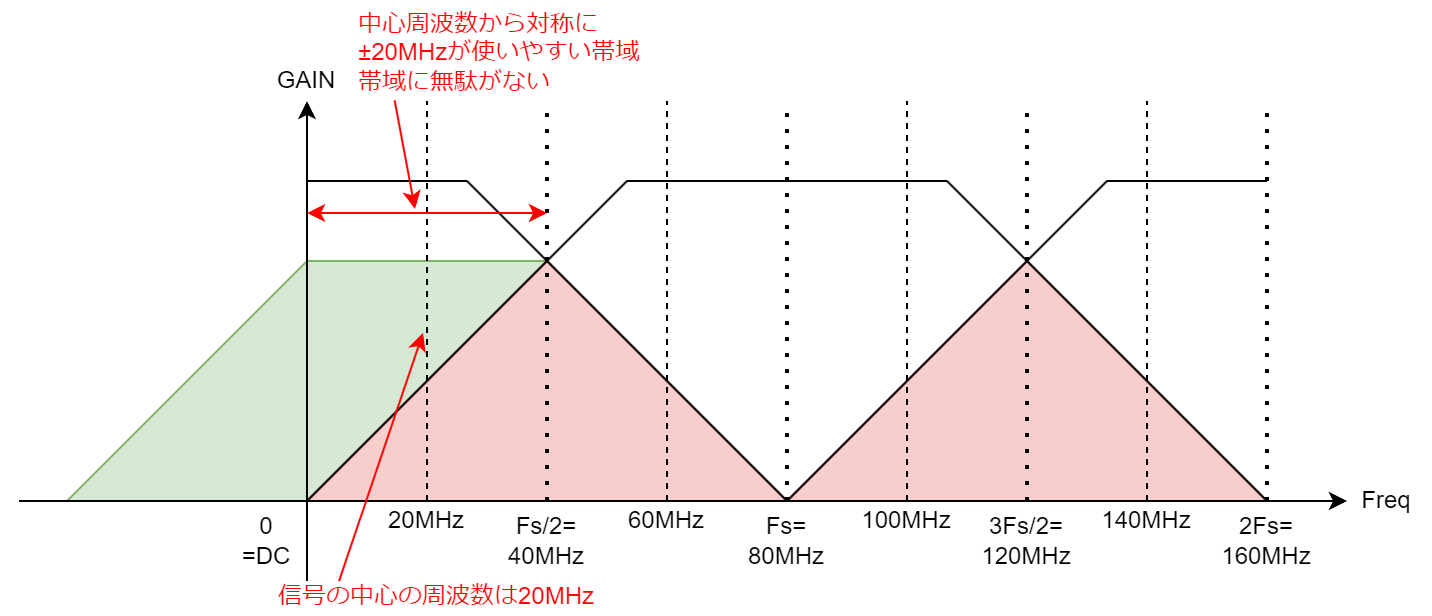
20MHzの信号でサンプリング周波数を60MHzに設定し、復元後の信号を逆相の100MHzとした場合を考えます。この場合、ナイキスト周波数の帯域幅が30MHzであるため、100MHzを中心とした信号を出力すると帯域幅は上下10MHzで合計20MHzとなります。(10MHzの余りが出ます。。。)
また、サンプリング周波数を80MHzに設定し、復元後の信号を同相の100MHzとした場合を考えます。この場合、ナイキスト周波数の帯域幅が40MHzであるため、100MHzを中心とした信号を出力すると帯域幅は上下20MHzで合計40MHzとなります。
以上の例の通り、サンプリングを行った際に考慮すべき帯域幅は、ナイキスト周波数に依存します。
ナイキスト周波数の範囲を確保できれば、エイリアシングを起こさずにサンプリングを行うことができる
というわけですね。
また、信号は同じ周波数帯域にあると衝突して区別出来なくなるので、占有できる周波数の帯域が決まっています。
「限られた周波数帯域をいかに無駄なく使うか」という観点 から、サンプリング周波数を80MHzに設定した方が「効率よく周波数帯域を使用している」ということになるわけですね。
フィルタ
電子回路では、周波数帯域を制限する回路のことを「フィルタ」と言います。
フィルタを使うことで、周波数の帯域を制限して、自分の取り出したい信号の帯域幅を確保します。
フィルタには
コンデンサやコイル、抵抗を使って実装する 「アナログフィルタ」
デジタル回路やソフトウェアで処理する 「デジタルフィルタ」
があります。
追記_2024/12/21
以下に、フィルタの分類について示します。
アナログフィルタ
抵抗成分(R)、インダクタンス(L)、キャパシタンス(C)のいずれかで構成されるフィルタのことです。
基本的には、抵抗器、コイル、コンデンサを使って構成されます。
高周波回路の場合は、プリント基板の配線にあるインピーダンスが無視できないため、これを使ってLCフィルタを構成することがあります。
また、アナログフィルタには
フィードバックを行わない 「パッシブフィルタ」
フィードバックを使用する 「アクティブフィルタ」
があります。
参考：アナログフィルタの基本_(株)エヌエフ回路設計ブロック
LCフィルタ
インダクタンス(L)とキャパシタンス(C)で構成されるフィルタです。
抵抗成分(R)が小さいため、無関係な周波数帯域での減衰を小さくできますが、インダクタンスを稼ぐために大きめのコイルが必要となるため、低周波での小型化は難しくなります。
対して、高周波回路の場合は、配線でインダクタンスが増加するため、利用されることがあります。
CRフィルタ
抵抗成分(R)とキャパシタンス(C)で構成されるフィルタです。
抵抗とコンデンサの定数で調整可能なため、小型化が可能です。
ただし、抵抗の定数によっては電圧降下が大きくなることや電流が大きくなることによって、ノイズを発生させたり、不要な減衰を起こすため、使い方を考える必要があります。
RLCフィルタ
抵抗成分(R)とインダクタンス(L)とキャパシタンス(C)で構成されるフィルタのことです。
抵抗成分(R)があるため、減衰に気を付ける必要がありますが、インダクタンス(L)とキャパシタンス(C)の定数を現実的な値に軽減できます。
デジタルフィルタ
ソフトウェアの計算やデジタル回路の構成によって実現するフィルタです。
IIRフィルタ
インパルス信号(離散値)を無限個並べようとするフィルタです。掛け算(乗算器)を使って実現します。
アナログフィルタを模擬することができます。
しかし、ソフトウェアの計算は有限の値で打ち切るため、IIRフィルタの理想的な特性を得ることができません。
FIRフィルタ
インパルス信号(離散値)を有限個並べようとするフィルタです。掛け算(乗算器)を使って実現します。
ソフトウェアの計算は有限の値で打ち切るため、計算と同等の特性を得ることができます。
ただし、有限な値で計算を打ち切るため、IIRフィルタに比べて急峻な特性を求めるのが難しいです。
CICフィルタ
足し算(加算器)のみで実現可能なフィルタです。
FIRフィルタに比べると急峻な特性を得ることができませんが、他のデジタルフィルタに比べると構造が簡素なため、よく用いられます。
デジタルフィルタの例
以下にデジタルフィルタにて構成可能なフィルタを示します。
ローパスフィルタ(LPF)
遮断周波数からDCまでを通すフィルタです。
遮断周波数を中心にして、低い周波数を通すので、ローパスと言います。
ハイパスフィルタ(HPF)
遮断周波数から高調波側を通すフィルタです。
遮断周波数を中心にして、高い周波数を通すので、ハイパスと言います。
バンドパスフィルタ(BPF)
遮断周波数が2つあるフィルタです。
遮断周波数の間の信号のみ通すので、バンドパスと言います。
バンドエリミネーションフィルタ(BEF)
遮断周波数が2つあるフィルタです。
遮断周波数の間の信号のみ 通さない ので、バンドエリミネーションと言います。
デシメーションフィルタ6
サンプリングレートを下げる(ダウンコンバートする)ローパスフィルタです。
間引きフィルタとも言います。
ローパスフィルタで帯域を制限して、サンプリングデータのゲインを一定間隔で0に落とした後、サンプリングデータを捨てます。
したがって、サンプリングレートを整数分の1倍にすることができます。
ADCのデジタル側に付けることで、デジタルデータのサンプリングレートをさらに低くすることができます。
たとえば、サンプリング周波数100MHzでサンプリングした信号の場合、1/2倍のデシメーションフィルタを通せば、サンプリング周波数50MHzでサンプリングしたことと等価になります。
なぜデシメーションフィルタが必要になるかというと、デジタル信号を処理するデジタル回路の動作速度が500MHzくらいで上限となっているためです。
500MHzを超えて動作させることができないため、デシメーションフィルタでサンプリング周波数を低くしてデジタル信号を処理するわけですね。
インターポレーションフィルタ6
サンプリングレートを上げる(アップコンバートする)ローパスフィルタです。
補間フィルタとも言います。
ゲインが0のサンプリングデータを追加した後、追加したサンプリングデータによって発生した折り返し雑音を取り除くためにローパスフィルタをかけて帯域を制限して、追加したサンプリングデータのゲインを0から持ち上げます。
したがって、サンプリングレートを整数倍にすることができます。
DACのデジタル側に付けることで、DACから出力する信号周波数を高くしたり、オーバーサンプリングしたりすることができます。
たとえば、サンプリング周波数100MHzでサンプリングした信号の場合、2倍のインターポレーションフィルタを通せば、サンプリング周波数200MHzでサンプリングしたことと等価になります。
なぜインターポレーションフィルタが必要になるかというと、デジタル信号を処理するデジタル回路の動作速度が500MHzくらいで上限となっているためです。
500MHzを超えて動作させることができないため、サンプリング周波数を低くしてデジタル信号を処理するわけですね。
出力するときには、信号の周波数を元に戻したいので、インターポレーションフィルタを使ってサンプリング周波数を高くするわけですね。
おわりに
自分はDACを使ったことがあまりないため、トンチンカンなことを言っているかもしれません。
どなたか、助言をいただけますと、助かります。。。
まあ、総評して「DACよくわからん」！！
追記_2024/12/22
申し訳ないのですが、NCOやらQMCやらDUCやらDDCやらの存在を忘れるという致命的なミスを犯しています。
そのため、記載されている内容を初期の内容から大幅に改変いたします。
インターポレーションフィルタは、サンプリング周波数を増やすことしか出来ません。そのため、インターポレーションフィルタの段数を増やしてもオーバーサンプリングの改善にしかなりません。
インターポレーションフィルタを通した後に、NCOやQMCを使って波形を整えてからDACに出力する必要があります。
アップコンバージョンでは、通常のDACの後段に様々なICを使用したり、「RF-DAC」のようなお高めのDACを使用したりすることになるため、応用する際には十分注意するようにしてください。