非再帰FFT

バタフライ演算

FFTは分割統治法の一種です。入力$2^n$個に対してデータを入れ替えながら演算を進めていきます。
$n = 3$の場合は以下の図の様になります。

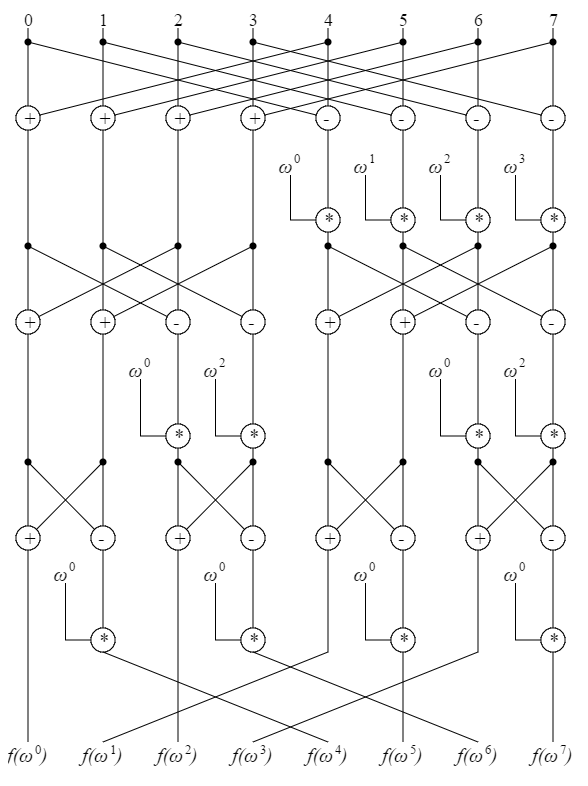
ここで$\omega$は体の性質を持った集合の元で、信号処理の場合は複素平面上の単位円の原始$n$乗根になり、モジュロ代数の場合は素数$p = 2^nk + 1$を成り立たせる最小の$k$に対し$n^k \bmod p$になります。
これをバタフライ演算と呼びます。
バタフライ演算は次の様に再帰関数を用いて実装される事が多い様です。

recursive-fft.cpp

#include <iostream>
#include <vector>
#include <complex>
#include <cmath>

using complex_t = std::complex<float>;
using seq = std::vector<complex_t>;

// 再帰FFT
template<bool Regular>
seq rec_fft(const seq &a){
    std::size_t n = a.size();
    if(n == 1){
        return a;
    }
    complex_t omega_n(std::cos(2.0 * M_PI / n), std::sin(2.0 * M_PI / n)), omega = 1.0;
    seq A(n / 2), B(n / 2);
    for(std::size_t i = 0; i < n / 2; ++i){
        if(Regular){
            A[i] = a[i * 2];
            B[i] = a[i * 2 + 1];
        }else{
            A[i] = complex_t(a[i * 2].real(), -a[i * 2].imag());
            B[i] = complex_t(a[i * 2 + 1].real(), -a[i * 2 + 1].imag());
        }
    }
    A = rec_fft<true>(A);
    B = rec_fft<true>(B);
    seq r(n);
    for(std::size_t i = 0; i < n / 2; ++i){
        r[i] = A[i] + omega * B[i];
        r[i + n / 2] = A[i] - omega * B[i];
        omega *= omega_n;
    }
    if(!Regular){
        for(auto &i : r){
            i /= n;
        }
    }
    return r;
}

int main(){
    // 入力列
    std::vector<float> input = { 0, 1, 2, 3, 4, 5, 6, 7 };

    // 複素数列に変換する
    seq input_complex(input.size());
    for(std::size_t i = 0; i < input.size(); ++i){
        input_complex[i] = input[i];
    }

    // 再帰FFT
    seq result_rec_fft = rec_fft<true>(input_complex);
    std::cout << "Recursive-FFT" << std::endl;
    for(auto &&n : result_rec_fft){
        std::cout << n << " ";
    }
    std::cout << std::endl;

    // 復元
    seq rev = rec_fft<false>(result_rec_fft);
    std::cout << "Inverse-FFT" << std::endl;
    for(auto &&n : rev){
        std::cout << n << " ";
    }

    return 0;
}

Recursiev-FFT
(28,0) (-4,-9.65685) (-4,-4) (-4,-1.65685) (-4,0) (-4,1.65685) (-4,4) (-4,9.65685) 
Inverse-FFT
(0,0) (1,1.19209e-07) (2,0) (3,-1.19209e-07) (4,0) (5,-1.19209e-07) (6,-0) (7,1.19209e-07) 

添え字ビット反転を導入する

バタフライ演算を解析すると、要素の入れ替えが次の木構造になっている事が分かります。

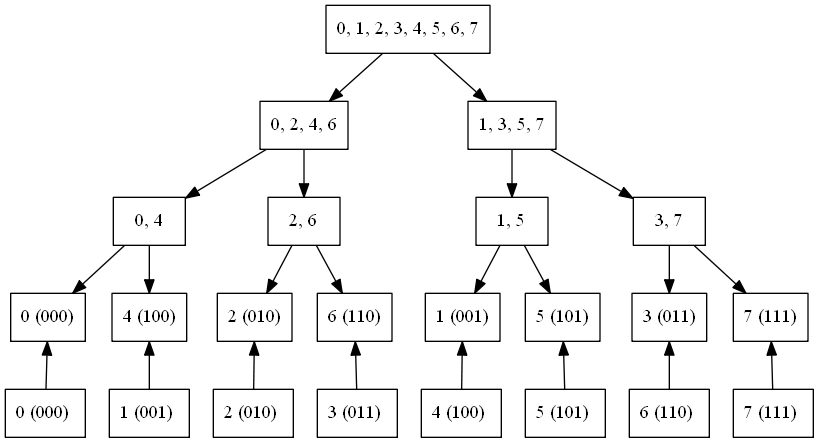
ここで0, 4, 2, 6, 1, 5, 3, 7を注意深く観察すると、それぞれ元のindexの2進数表現を最下位bitからn bitまで反転させただけになっています。
データの入れ替えはn回の再帰関数呼び出しからn/2回のループに置き換える事が可能な事が分かりました。
FFTの再帰関数による実装は末尾再帰最適化が効かず、入れ替えの度にスタックとヒープを確保・解法する手続きを行うので効率が悪いです。
以上の考察に基づいて書き直してみましょう。

iterative-fft.cpp

#include <iostream>
#include <vector>
#include <complex>
#include <cmath>

using complex_t = std::complex<float>;
using seq = std::vector<complex_t>;

// ビット長を得る
std::size_t bit_num(std::size_t t){
    std::size_t n = 0;
    while(t > 0){
        ++n;
        t >>= 1;
    }
    return n;
}

// ビット順序を反転する
int bit_rev(std::size_t a, std::size_t n){
    if(a == 0){
        return a;
    }
    std::size_t r = 0;
    // 長さが基数だった場合, 中央のbitを得る
    if(n % 2 == 1){
        r |= ((a >> (n / 2)) & 1) << (n / 2);
    }
    // 前後の順序を入れ替える
    for(std::size_t i = 0; i < n / 2; ++i){
        r |= ((a >> i) & 1) << (n - 1 - i);
        r |= ((a >> (n - 1 - i)) & 1) << i;
    }
    return r;
}

// ビットリバースコピー
void bit_rev_copy(const seq &a, seq &A, std::size_t n){
//    信号処理で窓を使う場合はこの時点で適用する
//    例:Vorbis窓
//    for(int i = 0; i < (1u << n); ++i){
//        float v = std::sin(M_PI * i / (1u << n));
//        v *= v;
//        A[bit_rev(i, n)] = a[i] * std::sin(M_PI * v / 2);
//    }

    for(std::size_t i = 0; i < (1u << n); ++i){
        A[bit_rev(i, n)] = a[i];
    }
}

template<bool Regular>
seq fft(const seq &a){
    seq A(a.size());
    std::size_t lg_n = bit_num(a.size()) - 1;
    std::size_t n = a.size();
    bit_rev_copy(a, A, lg_n);
    if(!Regular){
        for(std::size_t i = 0; i < n; ++i){
            A[i] = complex_t(A[i].real(), -A[i].imag());
        }
    }
    for(std::size_t s = 1; s <= lg_n; ++s){
        std::size_t m = 1 << s;
        complex_t omega_m(std::cos(2.0 * M_PI / m), std::sin(2.0 * M_PI / m)), omega = 1.0;
        for(std::size_t j = 0; j < m / 2; ++j){
            for(std::size_t k = j; k < n; k += m){
                complex_t t = omega * A[k + m / 2], u = A[k];
                A[k] = u + t;
                A[k + m / 2] = u - t;
            }
            omega *= omega_m;
        }
    }
    if(!Regular){
        for(std::size_t i = 0; i < n; ++i){
            A[i] /= n;
        }
    }
    return A;
}

int main(){
    // 入力列
    std::vector<float> input = { 0, 1, 2, 3, 4, 5, 6, 7 };

    // 複素数列に変換する
    seq input_complex(input.size());
    for(std::size_t i = 0; i < input.size(); ++i){
        input_complex[i] = input[i];
    }

    // 非再帰FFT
    seq result_fft = fft<true>(input_complex);
    std::cout << "Iterative-FFT" << std::endl;
    for(auto &&n : result_fft){
        std::cout << n << " ";
    }
    std::cout << std::endl;

    // 復元
    seq rev = fft<false>(result_fft);
    std::cout << "Inverse-FFT" << std::endl;
    for(auto &&n : rev){
        std::cout << n << " ";
    }
    return 0;
}

Iterative-FFT
(28,0) (-4,-9.65685) (-4,-4) (-4,-1.65685) (-4,0) (-4,1.65685) (-4,4) (-4,9.65685) 
Inverse-FFT
(0,0) (1,1.19209e-07) (2,0) (3,-1.19209e-07) (4,0) (5,-1.19209e-07) (6,-0) (7,1.19209e-07) 

参考文献

アルゴリズムイントロダクション（精選トピックス）