ローパスフィルターのチートシートです。
すべて逐次型の処理となります。
誰かのお役に立てれば幸いです。
一次のローパスフィルター
まずは1次から。
パラメータの換算方法を説明した後、本題のLPF計算を説明します。
時定数→カットオフ周波数の変換
単位はそれぞれ秒、Hzです。
f_c = \frac{1}{2\pi\tau}
import math
def tau_to_fc(tau_sec: float) -> float:
return 1 / (2 * math.pi * tau_sec)
カットオフ周波数→時定数の変換
単位はそれぞれ秒、Hzです。
\tau = \frac{1}{2\pi f_c}
import math
def fc_to_tau(fc_hz: float) -> float:
return 1 / (2 * math.pi * fc_hz)
時定数→alphaの変換
\alpha = 1 - e^{-\frac{dt}{\tau}}
import math
def tau_to_alpha(tau_sec: float, dt: float) -> float:
return 1 - math.exp(-dt / tau_sec)
1次のローパスフィルターの計算
それでは本題のLPF計算です。
最小構成
class LowPassFilter_1d_minimal:
def __init__(self, initial_value: float = 0.0):
self.y_prev = initial_value
def process(self, x: float, alpha: float) -> float:
self.y_prev = alpha * x + (1 - alpha) * self.y_prev
return self.y_prev
dt、時定数、カットオフ周波数を考慮した構成
import math
class LowPassFilter_1d:
def __init__(self, tau_sec: float, dt_sec: float, initial_value: float = 0.0):
"""
初期化:
- tau_sec: 時定数 [秒]
- dt_sec: サンプリング間隔 [秒]
- initial_value: 初期値
"""
self.dt_sec = dt_sec
self.y_prev = initial_value
self.update_alpha_by_tau(tau_sec)
def update_alpha_by_tau(self, tau_sec: float, dt_sec: float = None):
"""
alpha を 時定数 tau に基づき更新
Parameters:
- tau_sec: 時定数 [秒]
"""
if dt_sec is None:
dt_sec = self.dt_sec
self.alpha = 1 - math.exp(-dt_sec / tau_sec)
def update_alpha_by_fc(self, fc_hz: float, dt_sec: float = None):
"""
alpha を カットオフ周波数 fc に基づき更新
Parameters:
- fc_hz: 周波数 [Hz]
"""
if dt_sec is None:
dt_sec = self.dt_sec
self.alpha = 1 - math.exp(-dt_sec / fc_hz)
def process(self, x: float) -> float:
"""
現在の入力 x を計算し、フィルタ後の値を返す。
"""
y_new = self.alpha * x + (1 - self.alpha) * self.y_prev
self.y_prev = y_new
return y_new
if __name__ == '__main__':
lpf = LowPassFilter_1d(tau_sec=0.2, dt_sec=0.01, initial_value=0.0)
lpf.update_alpha_by_tau(2.0)
filtered_value = lpf.process(12.3)
フィルタリングの計算そのものは下記の1行なのですが...。
y_new = self.alpha * x + (1 - self.alpha) * self.y_prev
時定数での近似式
時定数tauから計算するときは以下のような近似式でもLPF計算できます。
dt_secがtau_secに比べて十分に小さい場合に有効です。(1/10とか)
正直言えばこれが一番使いやすいです。
class LowPassFilter_Approximation:
def __init__(self, tau_sec: float, dt_sec: float, initial_value:float = 0.0):
self.tau_sec = tau_sec
self.dt_sec = dt_sec
self.y_prev = initial_value
def process(self, x):
self.y_prev = self.y_prev + (self.dt_sec / self.tau_sec) * (x - self.y_prev)
return self.y_prev
if __name__ == "__main__":
lpf = LowPassFilter_Approximation(20.0,1.0)
filtered_value = lpf.process(12.3)
1次LPFでの結果
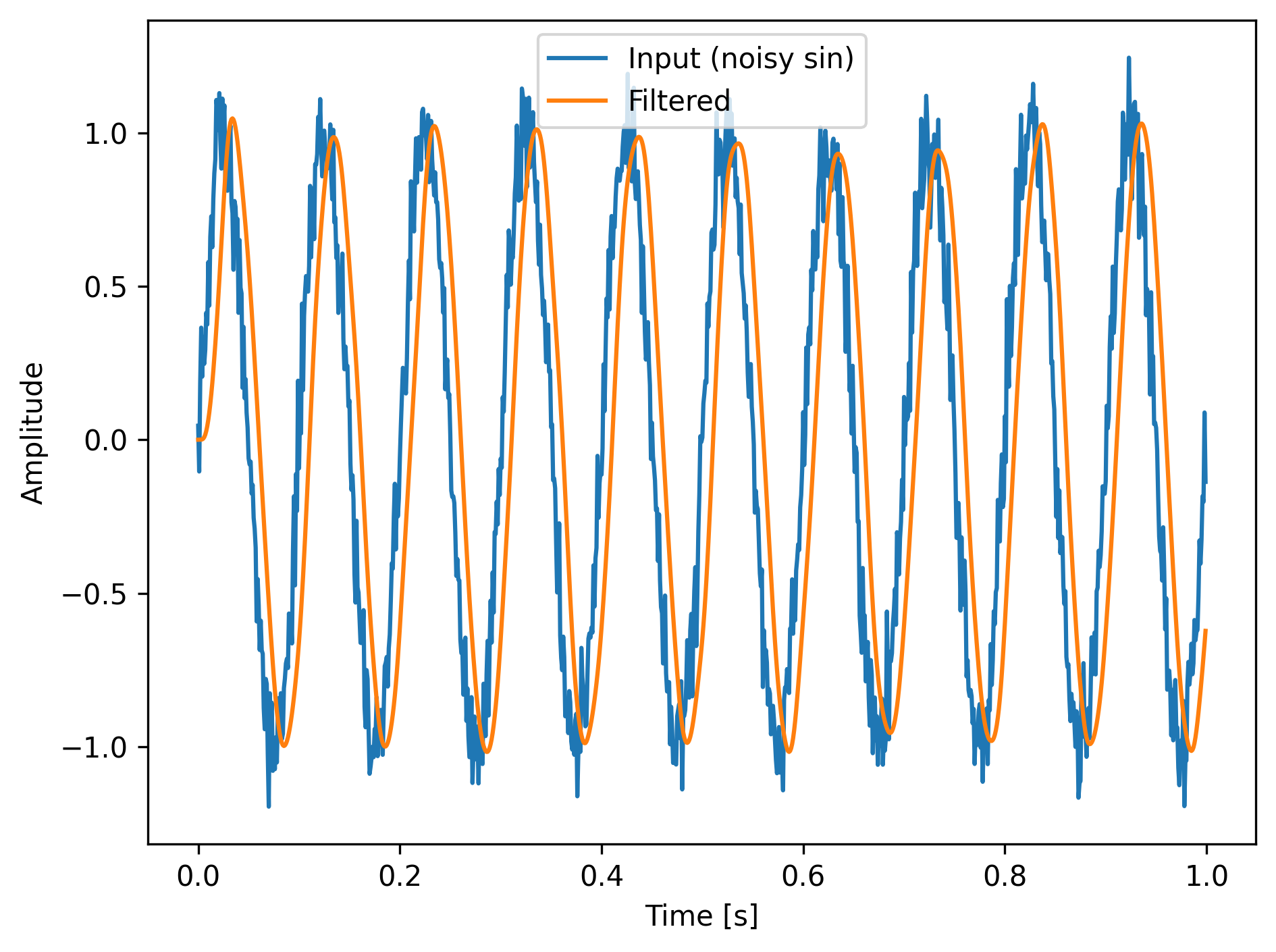
適当なサイン波形を準備して表示しました。
それらしくなっていますね。
n次のローパスフィルターの計算
続いてn次のローパスフィルターです。今回は4次のローパスフィルターで解説します。
こちらもパラメータ計算→LPF計算の順で説明します。
バターワース特性のパラメータ計算
パラメータはscipyで計算することをおすすめします。
import math
from scipy import signal
order = 4 #次数
cutoff_hz = 40 # カットオフ周波数[Hz]
dt_sec = 0.001 #dt[秒]
# サンプリング周波数(Hz)の計算
fs = 1 / dt_sec
# 正規化されたカットオフ周波数
normalized_cutoff = cutoff_hz / (fs / 2.0)
# バターワースフィルタ係数を計算
b, a = signal.butter(order, normalized_cutoff, btype='low', analog=False)
# besselフィルタの場合
# b, a = signal.bessel(order, normalized_cutoff, btype='low', analog=False)
print(f"b:{b}")
print(f"a:{a}")
b:[6.24184139e-14 2.49673656e-13 3.74510484e-13 2.49673656e-13 6.24184139e-14]
a:[ 1. -3.99738687 5.99216404 -3.99216745 0.99739029]
a[0]==1となってますが、ここのパラメータは使わないので無視される部分ですね。
n次のローパスフィルタ計算
リングバッファ処理をしたかったので、dequeを使ってリストを管理しています。
配列を使用した例
import math
import random
import matplotlib.pyplot as plt
from scipy import signal
from collections import deque
class LowPassFilter_nd:
def __init__(self, order, fc, dt_sec):
"""
n次元のローパスフィルター
Parameters:
order : フィルタ次数(ここでは4)
fc : カットオフ周波数(Hz)
dt_sec : 時間ステップ(秒)
"""
self.order = order
self.dt_sec = dt_sec
# フィルタ係数を計算
self.update_alpha_by_fc(fc, dt_sec)
# 逐次処理用バッファ(deque化)。要素数は order+1 個
self.x_history = deque([0.0] * (self.order + 1), maxlen=(self.order + 1))
self.y_history = deque([0.0] * (self.order + 1), maxlen=(self.order + 1))
def update_alpha_by_fc(self, fc: float, dt_sec: float = None):
"""
alpha を 時定数 tau に基づき更新
Parameters:
- fc: カットオフ周波数 [Hz]
"""
if dt_sec is None:
dt_sec = self.dt_sec
# カットオフ周波数(Hz)の計算
cutoff_hz = fc
# サンプリング周波数(Hz)の計算
fs = 1 / dt_sec
# 正規化されたカットオフ周波数
normalized_cutoff = cutoff_hz / (fs / 2.0)
# バターワースフィルタ係数を計算
self.b, self.a = signal.butter(self.order, normalized_cutoff, btype='low', analog=False)
# besselフィルタの場合
#self.b, self.a = signal.bessel(self.order, normalized_cutoff, btype='low', analog=False)
def process(self, x):
"""
IIRフィルタを 1サンプル単位で逐次処理する。
差分方程式 (4次の場合):
y[n] = b[0]*x[n] + b[1]*x[n-1] + ... + b[4]*x[n-4]
- a[1]*y[n-1] - ... - a[4]*y[n-4]
(a[0] = 1)
deque の先頭 (index=0) が最新サンプル。
"""
# 新しい入力サンプルを先頭に追加
self.x_history.appendleft(float(x))
# 差分方程式で出力を計算
y = 0.0
# b[k] * x[n-k] の加算 (ただし deque[0] は x[n], deque[1] は x[n-1], ...)
for k in range(self.order + 1):
y += self.b[k] * self.x_history[k]
# -a[k+1] * y[k] の減算 (k=1..order; a[0]は1)
for k in range(self.order):
y -= self.a[k+1] * self.y_history[k]
# 新しい出力サンプルを先頭に追加
self.y_history.appendleft(float(y))
return y
if __name__ == "__main__":
# パラメータ設定
order = 4 # フィルタ次数
dt_sec = 0.001
fc = 40
# LPFクラスのインスタンス化
lpf = LowPassFilter_nd(order=order, fc=fc, dt_sec=dt_sec)
# テスト信号
# 周波数10Hzの正弦波に雑音を加える例
freq_signal = 10.0
num_samples = 1000
time_list = []
input_signal_list = []
output_signal_list = []
for n in range(num_samples):
t = n * dt_sec
# ノイズ付き正弦波: sin(2π f t) + 雑音
pure_sin = math.sin(2.0 * math.pi * freq_signal * t)
noise = random.gauss(0.0, 0.1) # 平均0, 標準偏差0.3 のガウスノイズ
x = pure_sin + noise
# 逐次フィルタ
y = lpf.process(x)
# グラフ用
time_list.append(t)
input_signal_list.append(x)
output_signal_list.append(y)
# --- グラフ描画 ---
plt.plot(time_list, input_signal_list, label="Input (noisy sin)")
plt.plot(time_list, output_signal_list, label="Filtered")
plt.xlabel("Time [s]")
plt.ylabel("Amplitude")
plt.legend()
plt.tight_layout()
plt.savefig("test.png", dpi=300, bbox_inches='tight')
plt.show()
配列を使わない例
上記のリスト(配列)計算を展開した場合の例です。
一部のPLCや制約が多い組み込み系において、配列を使わずに計算するという需要が僅かにあると思います。...ありますよね?ということで参考コードを紹介します。pythonでの実装ですがc言語やStructured Text、ラダーなど所望の環境で実装し直してください。四則演算なのでそれほど難しくないと思います。
もし2次、3次を所望の場合は次数に応じてフィルタリング計算部を消してください。
フィルタ係数a,bの自前での計算は流石に難しいので、事前にscipyで計算してa_0・・・ b_0・・・にそれぞれ与えることにします。
import math
from scipy import signal
order = 4 #次数
cutoff_hz = 50 # カットオフ周波数[Hz]
dt_sec = 0.001 #dt[秒]
# サンプリング周波数(Hz)の計算
fs = 1 / dt_sec
# 正規化されたカットオフ周波数
normalized_cutoff = cutoff_hz / (fs / 2.0)
# バターワースフィルタ係数を計算
b, a = signal.butter(order, normalized_cutoff, btype='low', analog=False)
print(f"b:{b}")
print(f"a:{a}")
b:[0.0004166 0.0016664 0.0024996 0.0016664 0.0004166]
a:[ 1. -3.18063855 3.86119435 -2.11215536 0.43826514]
b_0 = 0.0004166
b_1 = 0.0016664
b_2 = 0.0024996
b_3 = 0.0016664
b_4 = 0.0004166
a_1 = -3.18063855
a_2 = 3.86119435
a_3 = -2.11215536
a_4 = 0.43826514
b_0 = 0.0004166
b_1 = 0.0016664
b_2 = 0.0024996
b_3 = 0.0016664
b_4 = 0.0004166
a_1 = -3.18063855
a_2 = 3.86119435
a_3 = -2.11215536
a_4 = 0.43826514
x_4 = 0.0
x_3 = 0.0
x_2 = 0.0
x_1 = 0.0
y_4 = 0.0
y_3 = 0.0
y_2 = 0.0
y_1 = 0.0
def process(x):
global x_1, x_2, x_3, x_4, y_1, y_2, y_3, y_4 # ←の変数をprocess関数内で使うためのおまじない
#フィルタリング計算
y = ( b_0 * x
+ b_1 * x_1
+ b_2 * x_2
+ b_3 * x_3
+ b_4 * x_4
- a_1 * y_1
- a_2 * y_2
- a_3 * y_3
- a_4 * y_4 )
# 過去の値を更新
x_4 = x_3
x_3 = x_2
x_2 = x_1
x_1 = x
y_4 = y_3
y_3 = y_2
y_2 = y_1
y_1 = y
return y
if __name__ == "__main__":
#使い方の例:
for x in range(100):
y = process(x)
フィルタリング計算はこちらもシンプルですね。
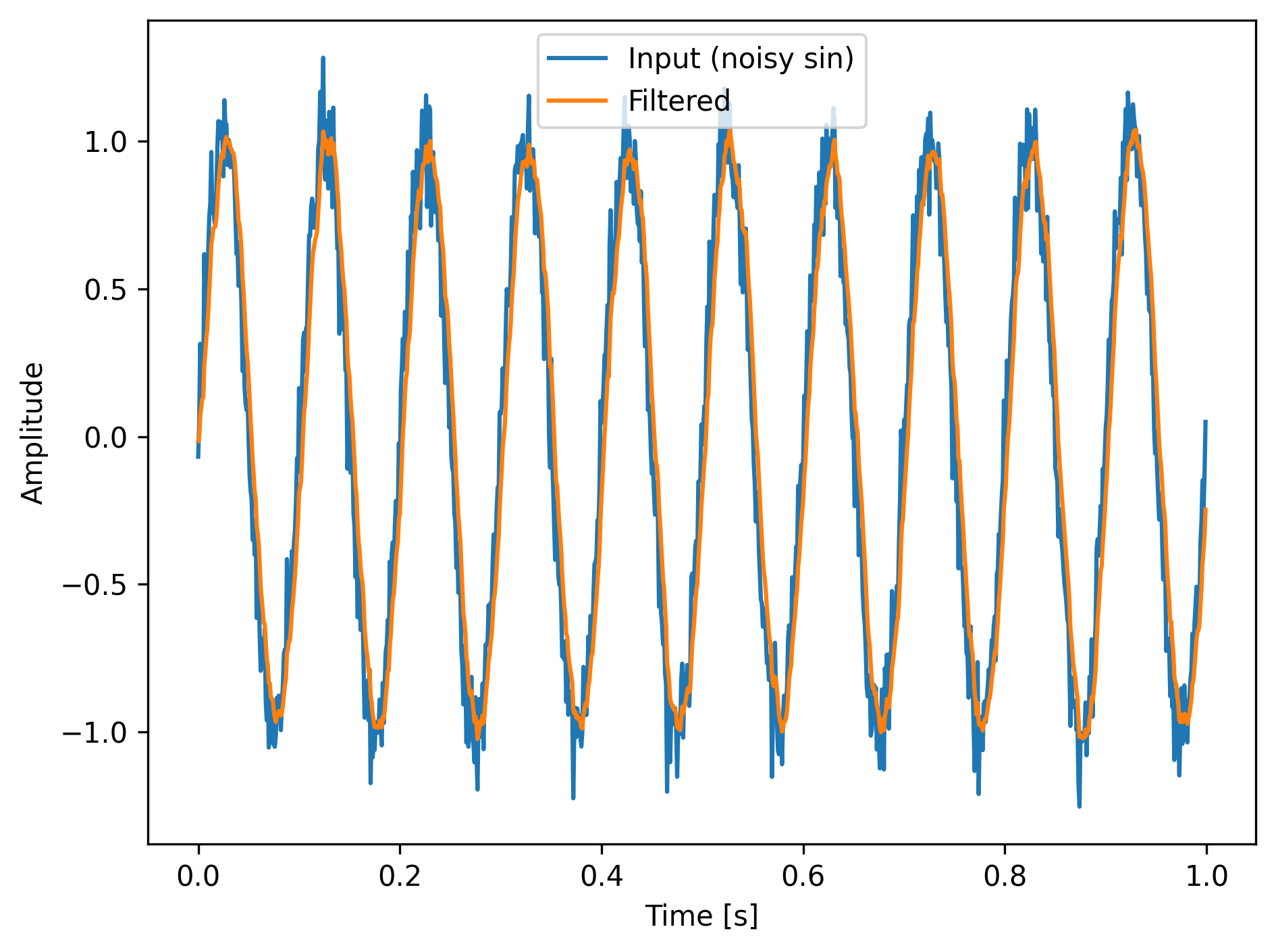
4次フィルタでの結果
1次と同じ設定ですが、こちらのほうが滑らか&遅れが大きいですね。
いい感じです。
n次でのフィルタ種類の選定
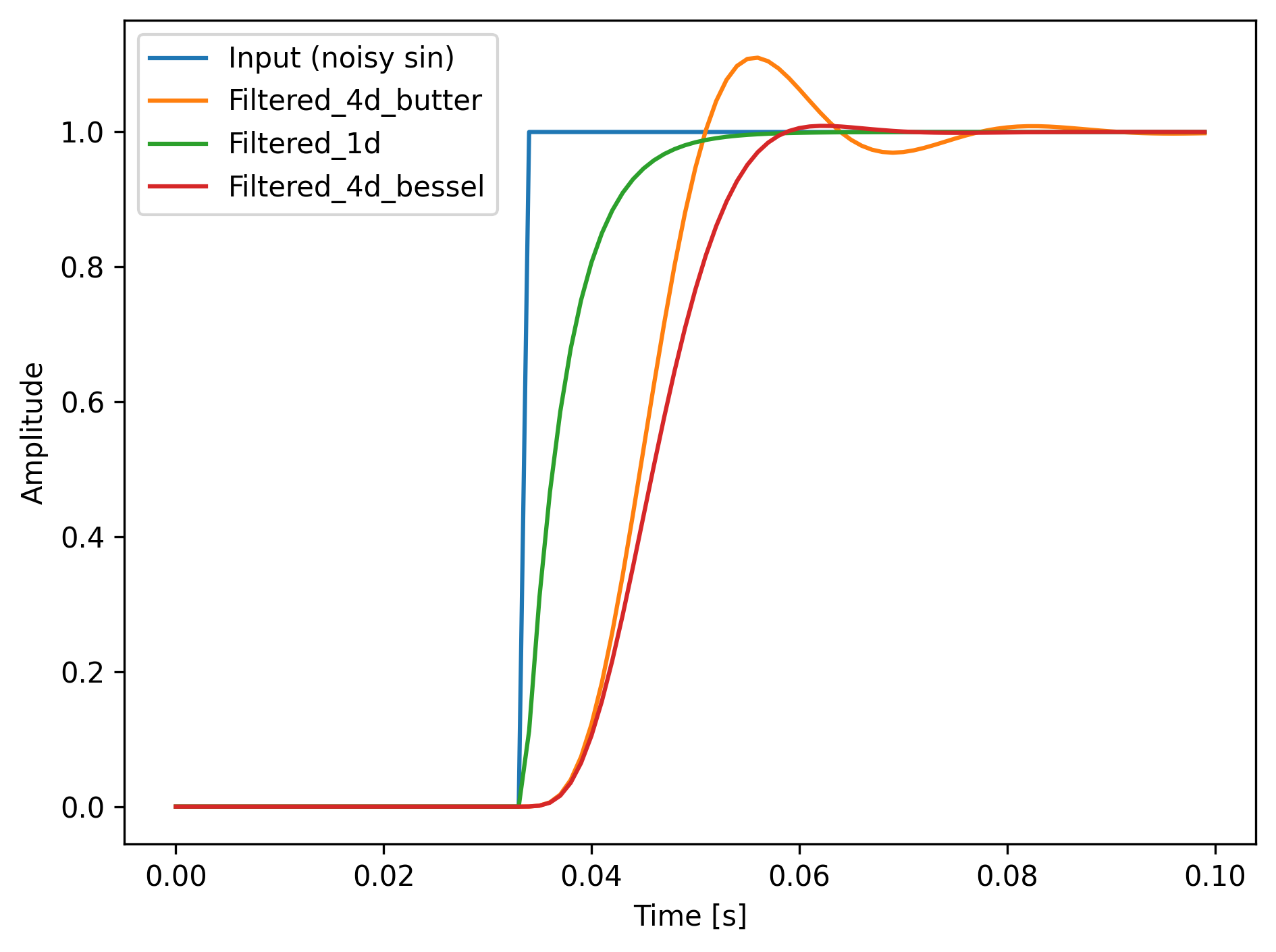
下図はステップ入力に対する応答です。
バターワースフィルタがステップ入力に対して大きくオーバシュートしているのがわかります。
今回のような逐次で使うほとんどの場合は制御だと思うので、あまり好ましい特性とは言えません。
1次元のLPFを使うか、ベッセルフィルタを試してみてください。
ベッセルフィルタへの変更は簡単で、以下のようにb,aを計算するだけです。
b, a = signal.bessel(order, normalized_cutoff, btype='low', analog=False)
あとは位相遅れとの相談してfcの選定を行ってください。
おわりに
ということで、ローパスフィルターのチートシートでした。
n次のフィルタ係数もMATLABを使わずとも、pythonだけで簡単に計算できて良い時代になりました。
あまり解説らしい解説をしていないコードだけの記事ですが、実践的と好意的に解釈していただけると幸いです。
誰かの役に立っているのかわからず手探りのオープンループ状態です。
いつ発散するかわからない(笑)ので、いいねなどでフィードバック頂けると励みになります。
他にも制御ライクな記事を書いていますので、興味があれば読んでみてください。
それではまた。