【AtCoder】ABC204をPython3で解説

ABC204の解説。

A - Rock-paper-scissors

解説

3人がじゃんけんしてあいこになった。2人の手からもうひとりの手を推測する問題。

0はグー、1はチョキを、2はパーとすると、全手の合計が3になるので、2人の手を引いたものがもう1人の手となる。

また、全員同じ手の場合は、誰か1人の手を出力すれば良い。

コード

x, y = map(int, input().split())
 
if x != y:
    print(3-(x+y))
else:
    print(x)

B - Nuts

解説

ある木の木の実が10個以上あれば、10個残して全部取る。これをN本の木に対して行うという問題。
コードもそのとおりに、木の実aが10より大きかったら、a-10した値をcntに加える。

コード

N = int(input())
A = map(int, input().split())
cnt = 0

for a in A:
    if a >= 10:
        cnt += a-10

print(cnt)

C - Tour

解説

スタート地点を固定したときゴール地点にできる都市の個数を数える問題。
この問題は、DFS（深さ優先探索） や BFS（幅優先探索） で求めることができる。今回は、公式解説を軸に、DFSで解説していく。

DFSについてそもそもわからないという方は、こちらの記事を先にご覧いただきたい。

コードに沿って解説したいので、先にコード。

# おまじない
import sys
sys.setrecursionlimit(10000)

# 入力の読み込み
N, M = map(int, input().split())
G = [[] for _ in range(N)]

# G[i] は都市iから道路で直接繋がっている都市のリスト
for _ in range(M):
    A, B = map(int, input().split())
    # Pythonではindex0始まりなので、都市iを-1して揃える
    G[A-1].append(B-1)

# 深さ優先探索（dfs）


def dfs(v):
    if seen[v]:
        return  # 同じ頂点を2度以上調べないためのreturn

    # 初期値でスタートをゴール地として設定 ex)(1, 1)をTrue
    seen[v] = True

    for vv in G[v]:
        dfs(vv)


ans = 0

# 都市iからスタートする場合
for i in range(N):
    # チェッカー
    seen = [False]*N
    # seen[j] は都市jに到達可能かどうかを表す
    dfs(i)
    # 都市iからの組み合わせ（True）の合計
    ans += sum(seen)

print(ans)

わかりやすいように入力例を示しながら説明する。入力例は、

5 4
1 2
2 3
2 4
1 5

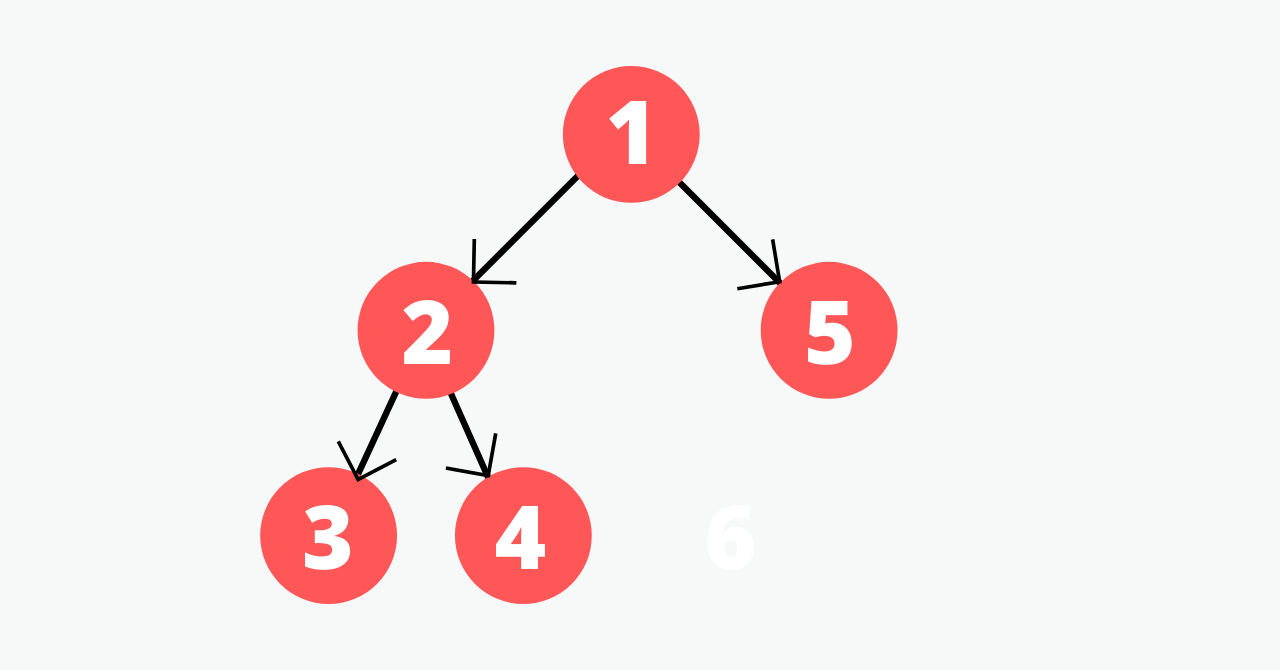
図で示すと、次のようになる。

まず、初期値設定として、Gを作る。GはGraphのG。これを都市の数Nだけリストを作りたいので、次のように書く。

G = [[] for _ in range(5)]

output
>> G: [[], [], [], [], []]

次に、A, Bのつながりを入力するわけだが、iがそもそも0スタートなので、初期値$A_1$, $B_i$と値がずれてしまう。したがって、i-1をして、扱いやすい形に整える。

for _ in range(4):
    A, B = map(int, input().split())
    G[A-1].append(B-1)

output
>> G: [[1, 4], [2, 3], [], [], []]

def dfs():は飛ばして、forの説明から。iにスタートとなる都市を入れる。ここで、チェッカーとして、seenを書いておく。

for i in range(4):
    seen = [False]*4
    ...

output
>> seen: [False, False, False, False]

話の大筋となる、DFS（深さ優先探索）。まず、seen[v] = Trueだが、例えば、この入力例であればまず、v = 0（都市1）が入る。したがって、seen: [True, False, False, False]となり、(1, 1)の判定となる。
次に都市1とのつながりを見たい。図を見ると、都市1とつながっているのは、都市2と都市5である。これはGに値が保存してあるので、ここから参照する。したがって、G[i-1]となるG[0]についてループを回す。
このとき同じ頂点で回さないように、if seen[v]: returnでseen[v]がTrueであれば、終わらせる。

dfs(0)のとき、つまり、都市1のスタートとゴールの組み合わせだが、普通に考えれば、都市1-5まで、どの都市でも組み合わせとして考えられる。まさにそのとおりで、このときのseenは、seen: [True, True, True, True, True]となっている。したがって、これをsum()足し合わせてあげることで、組み合わせを数えられる。

dfs(1)のとき、つまり、都市2のスタートとゴールの組み合わせは、都市2-4までが答えである。このときのseenは、seen: [False, True, True, True, False]でちゃんと対応した答えになっている。

これを全dfs(i)で計算して、数え上げたansが答えとなる。

コード

import sys
sys.setrecursionlimit(10000)

N, M = map(int, input().split())
G = [[] for _ in range(N)]

for _ in range(M):
    A, B = map(int, input().split())
    G[A-1].append(B-1)


def dfs(v):
    if seen[v]:
        return

    seen[v] = True

    for vv in G[v]:
        dfs(vv)

ans = 0

for i in range(N):
    seen = [False]*N
    dfs(i)
    ans += sum(seen)

print(ans)

編集後記

公式解説って全然わかりやすい解説になってないような...。