■時系列データの変化点検知を実装する
時系列データの変化点検知の手法を勉強したのでメモ。
問題設定
閾値を超えたときに異常を知らせる仕組みがある。
単発での閾値超えではなく、継続して閾値を超えた場合にのみ、
異常検知したいときがある。(サーバやサイトのレスポンスetc)
単純に閾値設定すると単発での閾値超えも拾ってしまい、
不要なアラートが発生することになる。
そこで、変化点検知の手法を用いて、
継続して閾値を超えた場合にのみ検知する手法を実装してみる。
手法
変化点検知の手法で、見つけたのは下記。 1
1.過去のデータから予測値を計算し、実測値と予測値の差を計算する方法
2.k近傍法を用いた手法
1で、SARIMAモデルから予測値を計算する方法に取り組んだが、
パラメータのチューニングが大変で、かつ実装もそこそこ面倒であるため、
今回は見合わせた。(実装が面倒だと業務に使いづらい)
この記事では、2.k近傍法を用いた手法に取り組んでみる。
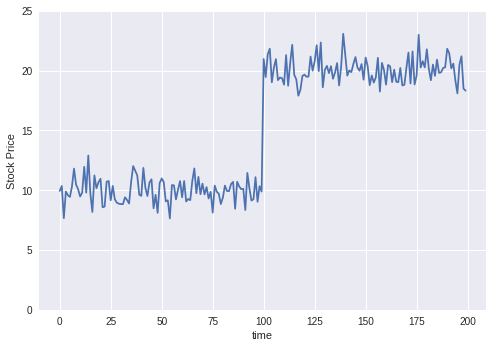
まず、データを用意する。
ある株価の時系列データと仮定。(あくまで仮)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# パラメータ
myu1=10 #異常発生前の平均
myu2=20 #異常発生後の平均
sd=1 #標準偏差
# 時系列データ 正規分布に従う時系列データをそれぞれ100個
data1 = np.random.normal(myu1,sd,100)
data2 = np.random.normal(myu2,sd,100)
# 可視化
data=np.hstack((data1,data2))
df = pd.DataFrame(data)
plt.plot(df)
plt.xlabel("time")
plt.ylabel("Stock Price")
K近傍法で学習する前に、部分時系列データを作る。
時間的に近いデータをまとめて作成する。
from sklearn.neighbors import KNeighborsClassifier
# 時間的に近いデータをまとめる。
x = data.reshape(1,-1) #shape(1,190)
M = 10
Train_data=x[:, 0:M] #shape(1,M)
for i in range(1, x.shape[1]-M):
X = x[:, i:i+M] #shape(1,10)
Train_data=np.vstack((Train_data,X))
Train_data.shape #(190, 10)
コードにある通り、xには時間iから時間i+Mまでの時系列データが格納されている。
iを0から(200-M)まで回して,Train_dataにxを連結して
Train_dataを作るので、Train_dataのサイズは(190,10)となる。
これは、データがM=10次元であり、それが190個あると考える。
K近傍法に食わしてみる。
clf = KNeighborsClassifier(n_neighbors=2) #近傍点(自分と自分以外)を探す
clf.fit(Train_data, np.zeros(Train_data.shape[0])) #ラベルはすべて0とする
dist, ind = clf.kneighbors(X)
distances=dist[:,1]
ちなみに中身はこんな感じ。
dist[:5,:]#dist:近傍点との距離 [自分, 自分の次に距離が近いデータ]
array([[0. , 1.37597833],
[0. , 1.38991142],
[0. , 1.60854258],
[0. , 1.61022187],
[0. , 1.94213876]])
ind[:5,:] #ind:近傍点の時間[自分, 自分の次に距離が近いデータ]
array([[ 0, 26],
[ 1, 27],
[ 2, 67],
[ 3, 68],
[ 4, 73]])
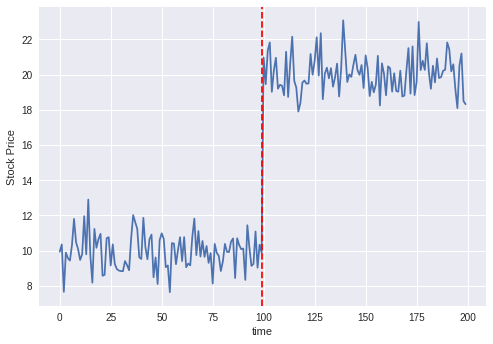
あとは下記のように、閾値を決め打ちして、変化点を見つける。
thred=8 #仮
henka=ind[distances > thred][-1,0]
plt.plot(df)
plt.axvline(x=henka, color='red', linestyle='--')
plt.xlabel("time")
plt.ylabel("Stock Price")
すると変化点検知ができる。
この手法を使うにあたって、
・閾値をトップダウンで決めないといけないこと。
データの傾向を考慮して、決め打ちで人間が設定することになる。
・変化点前後でのデータの平均に大きな差がない場合。
⇒データの標準偏差が大きい場合。
この場合は、上記の例のようにきれいに変化点を検知することができない。
なぜなら、自分の次に最も近い点を変化点付近と認識することが難しくなるためである。
⇒データの標準偏差が小さい場合。
どの程度小さいかによるが、検知はできるかと。
-
ほかにありましたら教えてください。 ↩