mem2regを解説してみる

はじめに

この記事は，まだmem2regのことをふんわりとしか理解していない人が書いています．間違いの指摘などお待ちしております．
また，この記事内では解説にLLVM-IRの前提知識を必要とします．(alloca, load, store, use-def chain などが何なのかわかっていればOK.)

mem2reg とは

mem2regはLLVMのPassの一つで，可能な限りメモリアクセスをレジスタアクセスへと変換します．
LLVMのPassとは言いますが，単にメモリアクセスをレジスタアクセスへと変換する機構のことだと思っていただければOKです．

mem2reg は大まかに何をするのか

ここからの解説は，主にこのあたりのコードに沿って進めていきます．

1. レジスタへと昇格できる alloca を集める.

   • どんなalloca? → load, storeからのみアクセスされていて，アドレスの取得などに利用されていない.
   • 以降のstore, loadはこれらのallocaを対象としたものとする

2. 簡単な場合を先に処理しておく

   • 一回しかstoreされていない場合
     • そのstore src, dst以降のload dstをすべてsrcで置き換えるだけ
   • 一つのBasic Block内でのみstore, loadされている場合
     • そのBasic Block内のstore, loadを実行順に歩いていって，load dstならその一つ前のstore src, dstのsrcに置き換えるだけ

3. それぞれのallocaについて，storeされるBasic Block (以降 def block)，loadされるBasic Block (以降 using block)を求め，これらを使い入口生存(live in)しているBasic Block(以降 livein block)を計算する

4. def blockの支配辺境にphiを挿入する．この時もlivein blockを使う．

5. プログラムの入口からBasic Blockを歩いていって，後続ブロックをたどりながらプログラムの出口にたどりつくまでに次のことを繰り返す．同じブロックをたどらないように注意．

   • store src, dstにたどり着いたら，srcを記録
   • load dstにたどり着いたら，その参照(use)を記録された値と置き換え
   • phiにたどり着いたら，記録された値をincoming nodeとして追加する． そしてphiを記録 (これらphiへの操作は同じブロックをたどって行うことがある)

6. 完成 (多分)

ちょっと詳しく解説

上の章の 3. と 4. と 5. について詳しく見ていきます．

3. について

入口生存

あるブロックの入口で変数が生存していること．
def blockとusing blockを求めてあるので，using blockから前任ブロックをたどっていってdef blockにたどり着くまでのすべてのブロックがlivein blockとなる．

4. について

支配・支配木

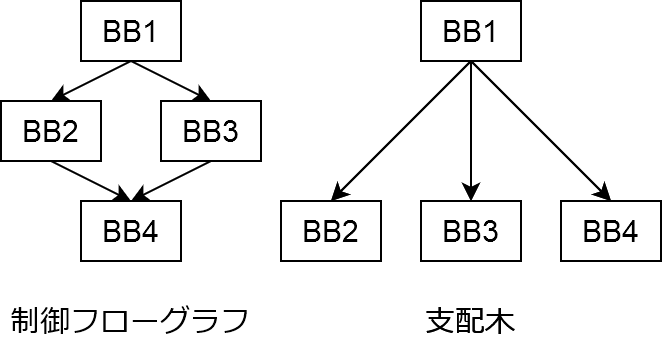
プログラムの入口からブロックB2に達するどの路も必ずブロックB1を通るとき，ブロックB1はブロックB2を**支配する(dominate)という．ブロックBは自分自身を支配することになっている．
また，支配関係は反射的かつ推移的であり，木の形で書くことができることが知られている．この木では，親のブロックが子孫のブロックを支配する．この木を支配木(dominator tree)**という．¹

画像で表すと次のようになる．

支配辺境

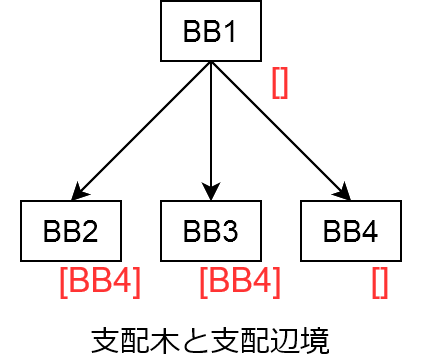
ブロックiの支配辺境（dominance frontier）とは，制御フローグラフ上で，初めてiの支配関係から「はずれた」ブロックjのことである．¹

画像で表すと次のようになる．ブロックの右下に示したのが支配辺境．先ほどの画像の制御フローグラフを参考にしてください．

支配辺境を求めるアルゴリズムにはいくつかありますが，LLVMは線形時間で解けるものを使っているようです²．

phi の挿入位置

phi を挿入するブロックは，あるdef blockの支配辺境であることが知られています¹．
とりあえず支配辺境の先頭に incoming node を持たない phi を挿入しておきましょう．

5. について

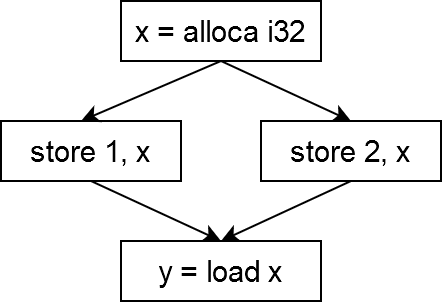
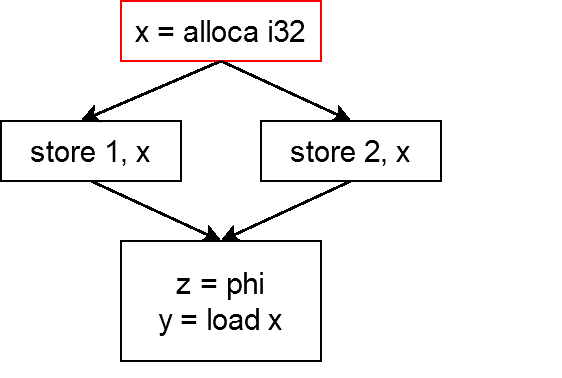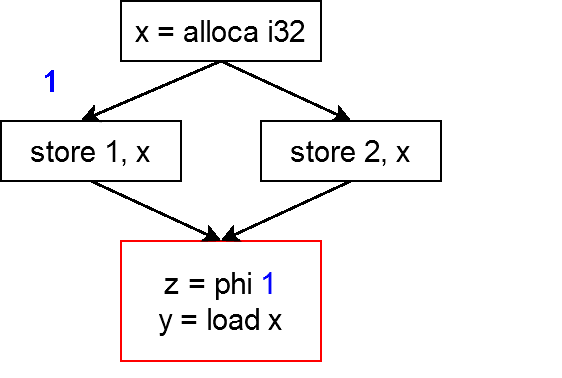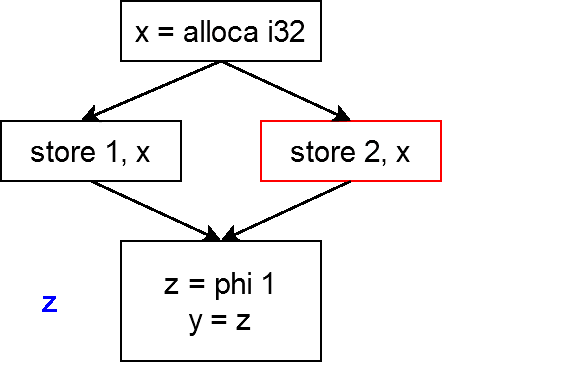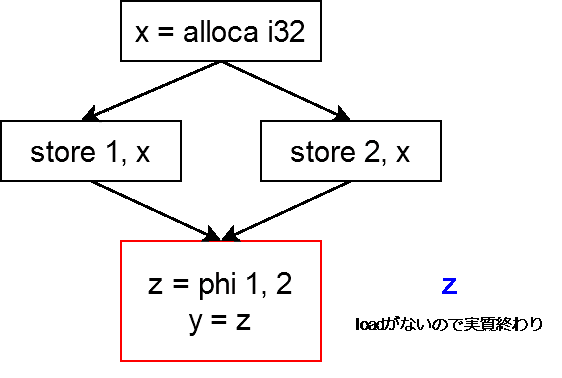
次のようなプログラムを考えます．

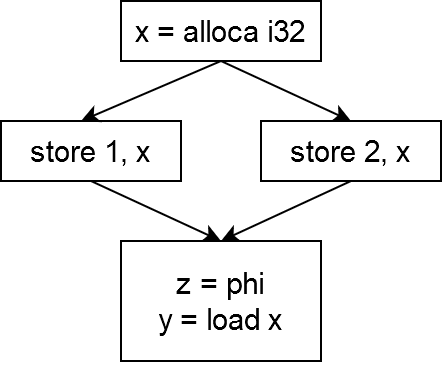
4.までの処理でphiが挿入されているので次のようになります．

プログラムの先頭からBasic Blockを歩いていきます．以下の点に注意しながらGIFを見てみてください．

• store src, dstにたどり着いたら，srcを記録

• load dstにたどり着いたら，その参照(use)を記録された値と置き換え
• phiにたどり着いたらincoming nodeとして記録された値を追加する. phiを記録

(TODO: GIF内で, loadの参照を置き換えるのではなく, load自体を置き換えてしまっている. 近いうちに直します...)

ここまで来たら，あとは alloca, store を削除してやれば完成です．(まあ途中で削除してもいいんですけどね)

最後に

この記事で紹介した手法で生成されるSSAはpruned SSAと呼ばれているようです．ほかにもSemi-pruned SSAなどがあり，まだあまりよく理解できていないので今後調べていきたい．

1. 静的単一代入形式を用いた最適化（導入編） とってもわかりやすい． ↩ ↩² ↩³

2. A linear time algorithm for placing φ-nodes. 実際にコードを読むとわかりやすい． ↩