モンテカルロ法で円の面積を近似的に計算してみる

やること

モンテカルロ法を利用することによって円の面積の近似解を得ることを目的とします。また、乱数の数が多いときと少ないときとで近似解の精度に違いが出るかを検証します。

どうやるか

実験にはpython3とMatplotlibを用いて計算します。円の半径は5とするため面積は5×5×3.14=78.5になり、この値に近いほど精度が高いといえます。例えば、座標平面上で(x,y)=(5,5)を中心とする円があるとき、0から10までの乱数を100個用意すると近似解の値はおおよそ78.0となります。

import matplotlib.pyplot as plt
import pylab
import random

x = []
y = []
random_number = 100 #乱数の個数を指定
for i in range(random_number): #座標をランダムに指定
    x.append(random.uniform(0, 10)) #x軸
    y.append(random.uniform(0, 10)) #y軸

area = 0
for i in range(random_number): #乱数が円の内側にあるかを判断
    if x[i]**2 + y[i]**2 <= 10**2: #三平方の定理
        area += 1
area = area/((i+1)/100.0) #すべての乱数のうち円の中にある乱数の割合

print('疑似乱数による円の面積は' + area)
print('計算による円の面積は' + 5*5*3.14)

#グラフを作成
pylab.figure('Area of a circle')
pylab.title('Area of a circle')
pylab.xlabel('X axis')
pylab.ylabel('Y axis')

#円の作成
t = pylab.arange(1000.)/1000 #0.1刻みで配列をつくる
x_en = 5*pylab.sin(2*pylab.pi*2*t)
y_en = 5*pylab.cos(2*pylab.pi*2*t)
pylab.plot(x_en+5, y_en+5, 'b') #円の線を青色に指定

pylab.plot(x, y, 'o', color="#ffa500")#乱数をオレンジ色に指定
pylab.show()

結果と検証

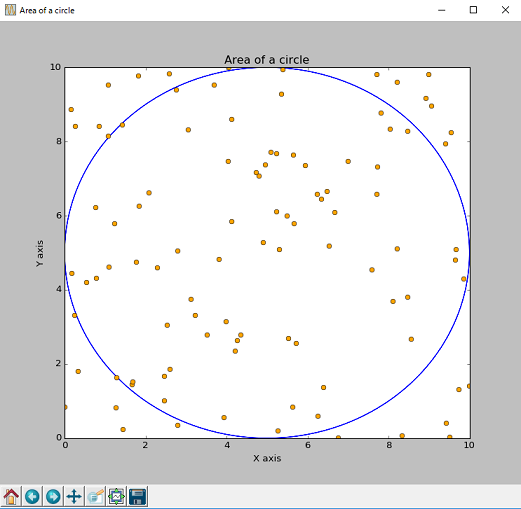
始めに乱数を100個用意して実験すると、近似解は79.0となりました。

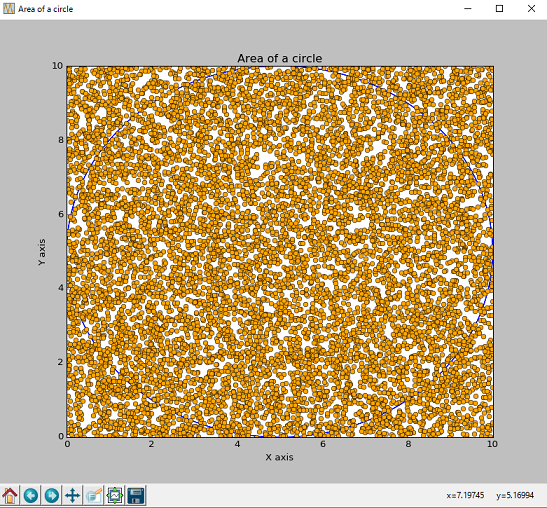
次に、乱数を10000個用意すると近似解は78.77となりました。

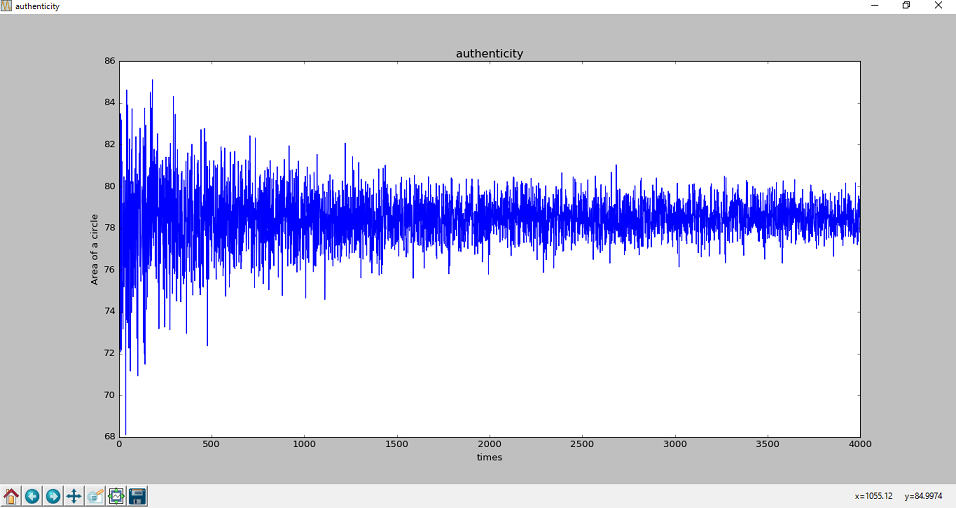
これだけでも近似解の精度が上がっていることが分かりますが、精度の向上を裏付けるため検証を施してみようと思います。検証では100個から4100個までの乱数を順次用意していくため、近似解を求める試行回数は4001回となります。

import pylab
import random

pseudo = []
simulation = 4000 #疑似乱数によって面積の近似解を求める試行回数
simulation = simulation + 101
for i in range(100, simulation):
    x = []
    y = []
    for j in range(i): #座標をランダムに指定
        x.append(random.uniform(0, 10))
        y.append(random.uniform(0, 10))

    area = 0
    for j in range(i): #乱数が円の内側にあるかを判断
        if x[j] ** 2 + y[j] ** 2 <= 10 ** 2: #三平方の定理
            area += 1
    area = area / ((i + 1) / 100.0) #すべての乱数のうち円の中にある乱数の割合
    pseudo.append(area)

#グラフの作成
pylab.figure('authenticity')
pylab.title('authenticity')
pylab.xlabel('times')
pylab.ylabel('Area of a circle')
pylab.plot(range(0, simulation-100), pseudo)
pylab.show()

作成したグラフをみると、試行回数を重ねるごとに近似解のばらつきが抑えられていき、だいたい78あたりに収束していることが分かります。