こんにちは、佐藤かえでです。
初めてQiitaの記事を書いています。
先日のAtCoderABC253-Dを解いていた際に、解法はあってるのになぜかACにならないということがありました。
だいたいこういうときは、floatとか小数点周りで誤差が出ているのでは?と思いいろいろ調べたのでここに記します。
AtCoderABC253 D
まずそもそもの問題からです。
D - FizzBuzz Sum Hard
問題文
1 以上 N 以下の整数であって、A の倍数でも B の倍数でもないものの総和を求めてください。
解法としては、
1~Nまでの総和から、同区間のAの倍数の総和、同区間のBの倍数の総和を引いて、
重複するAとBの最小公倍数の倍数の総和を足せばokです。
詳しくは解説を見てください。
解説
間違いのコードと正解のコード
わたしが最初に提出した間違いのコードはこのようになります。
import fractions
def wa(N):
Ans = int((N+1)*N/2)
return Ans
N,A,B=map(int,input().split())
S=0
ax=int(N/A)
bx=int(N/B)
G=int( A * B /fractions.gcd(A, B))
gx=int( N/(A * B /fractions.gcd(A, B)))
S=wa(N) -wa(ax)*A -wa(bx)*B + wa(gx)*G
print(S)
正解(AC)のコードはこちらになります
import fractions
def wa(N):
Ans = ((N+1)*N)//2
return Ans
N,A,B=map(int,input().split())
S=0
ax=N//A
bx=N//B
G= A * B //fractions.gcd(A, B)
gx=N//G
S=wa(N) -wa(ax)*A -wa(bx)*B + wa(gx)*G
print(S)
コード上での間違いの箇所は
##間違い
int( (n*1)*n/2 )
##正解
((N+1)*N)//2
です。
Pythonはint(N)でNの少数を切り捨てできるので、//と同じ結果になるはずです。
そこで、一体どんなNをwa(N)に入力すると、違いが発生するのかをAtCoderのコードテストで検証しました。
##Python3だと遅くて終わらないのでPyPy3で実行
for i in range(10**9):
if( (i+1)*i//2 != int((i+1)*i/2) ):
print(i,((i+1)*i)//2 , int((i+1)*i/2))
134217729 9007199456067585 9007199456067584
134217730 9007199590285315 9007199590285316
134217733 9007199992938511 9007199992938512
134217734 9007200127156245 9007200127156244
134217737 9007200529809453 9007200529809452
...
答えが9007199456067584より大きい数字で起きることがあることがわかりました。
ここでおそらく型の問題だなあと思いました。
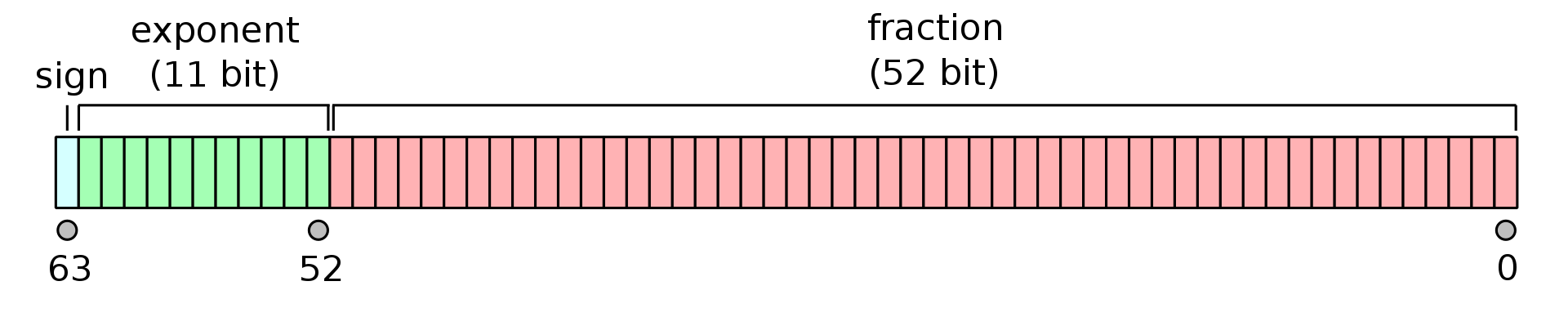
Floatのこと IEEE754 double
PythonのFloatはC++でいうところのDoubleです。
これはIEEEで決まっていて、64bitに対して以下のようなデータ構造与える方法です。
Float = (-1)^{Sign}\times1.fraction\times10^{exponent-11 1111 1111}\\
-----------------
\\
ex)\\
sign=0\\
fraction = 1000 ... 0000\\
exponent = 100 0000 0011\\
Float = (-1)^{0}\times1.1000...0000\times10^{100 0000 0011 - 11 1111 1111}\\=24_{(10)}
ここで注目したいのが、仮数部(fraction)が52bitということです。
試しに$2^{53}$を計算してみると (仮数部は1.nを表しているため)
$2^{53}=9,007,199,254,740,992$
デジャブ感がありますね。
なぜこの数字を超えると、バグが出るのかそれを考えてみます。
Floatの精度
結論から言うと
$2^{53}-1$より大きい数字は1刻みではなく、2刻み、4刻みでしか表現できません。
これがFloatの精度です。
原理としては単純です。
仮数部の最大値である1.111...1111に対して、$2^{52}$をかけると、指数部の小数点が右へ52回移動するため、ちょうど整数になります。
この数字が$2^{53}-1=9,007,199,254,740,991$となります。
今回の問題の場合、$n(n+1)$は偶数のため、$2^{54}$までは正しくfloatで表現できます。
for i in range(10**9):
if( (i+1)*i > 2**54 ):
break
elif( (i+1)*i//2 != int((i+1)*i/2) ):
print(i,((i+1)*i)//2 , int((i+1)*i/2))
試しにコレを回すと、何も出力されません。2**55にすると出てきます(それはそう)
そして、問題となった9007199456067585について /1をすることでfloatの挙動を観察すると
A=9007199456067585
print(A/1)
print(A+1/1)
print(A+2/1)
print(A+3/1)
9007199456067584.0
9007199456067584.0
9007199456067586.0
9007199456067588.0
となります。
なんでこのような出力になるのかは厳密にはわかりませんがPythonは小さい方に丸められるらしいので、
...86/1の際は丸めで84へ、...87/1の際も丸めで86へっていうことでしょうか。
...86/1の丸めが納得いきませんが多分そうなんでしょう。
まとめ
なんでこんな丸め方になるのかはわからないのですが、とりあえずint(a/b)とa//bの違いについて
基本はa//bを使うっていうことがわかりました。
a//bは素直にintで計算してくれます。
ううう・・・D問題行けたのに・・・
コレのせいでレート下がりました・・・