大歓喜
ついにこのソフトを公開する事ができました!
これまでの悲しみの履歴
*とても悲しい追記 2022.7.25 なんてこった! 本記事のWavelet変換のソフトは諸事情により非公開で決定になってしまいました。 まぁ、無名の個人がOSS作ったところでたかが知れてるってことです…(´・ω・`)*注意
本記事で紹介している俺のWavelet変換パッケージことninwavelets/忍者之漣は諸事情により一旦非公開にしています。
現在準備中で、なんとか2020年〜2021年初旬には公開に漕ぎ着けたいと思っています。
*重大な追記 2020.12.10
頭悪い間違いを書いていたので修正しました。
本記事について
フーリエ変換から、CWT前提にしたGabor/Morlet/GMWまでをまとめます。
ただし、当然僕の理解の範囲内かつ、解析屋さんの視点での話です。
初めの方はフーリエの基礎っぽい所ですが、言いたいのはMorlet→GMW辺りの話です。
まず、オイラーの公式があった
18世紀のなかば、オイラーの公式が発見されました。
$$e^{ix}=cosx + isinx$$
これは数ある数学の公式の中でも最も美しい公式の一般化であり、人類の宝であります。
研ぎ澄まされたかのような美しさの中に、豊かな応用が活きる素晴らしい式です。
wikipedia オイラーの公式
そして、いかにその公式が美しいかは下記に熱弁されています。
wikipedia オイラーの等式
この式はフーリエ変換関連の全ての前提となります。
故に、波形解析やる初心者には僕は必ず「オイラーの公式を崇めよ👹」と伝えています。
そしてフーリエ変換が生まれた
ジョセフ・フーリエ先生という人がフーリエ変換を19世紀はじめ頃発見したそうです。
波をsinとcosの足し合わせだけで表現するというやつですな。
よほどやばい波(例えば、延々と増大し続けるとか)じゃなければフーリエ変換で全部表せます。
これ、オイラーの公式から導出できるんです。
超簡単に言うと、波(永遠に続くやつ限定)を
波(振幅X時間) → フーリエ級数(周波数X複素数)
という風にフーリエ級数という形にするものです。
始めっから複素級数だったかどうかは僕は知らないですが、複素数というのが重要です。
応用:窓フーリエ
フーリエ変換は元来永遠に続く波限定という超絶面倒くさい性質を持っています。
なら、**波の一部を区切って、それが永遠に続くと仮定して計算すれば
有限の波のフーリエ変換が算出できますね?**簡単だね?
しかし、落とし穴があります。一部の波を切り取ったら切り取り面が
低周波から超高周波までの合算として解釈されてしまうのです。
切り取り面は常に0でなければおかしくなります。
そのため、窓関数という物を掛け算して両端を0にするのが定石となっています。
さて、このように一部切り出してフーリエ変換したとして…短く切った場合に
解析結果(周波数解像度)が正確じゃなくなる事は直感的に分かるかと思います。
一方、長く切った場合はその「長い時間での解析」しか出来ず、時間が荒くなります。
このように、あっちを立てればこっちが立たないのを不確定性原理といいます。
この、窓関数問題を解決したのが本記事のテーマであるwavelet変換ですが、後述します。
スペクトル
フーリエ変換すると、複素数が算出されます。
複素数というのは極座標で表せます。
$$acosx+iasinx=r(\theta)$$
つまり、rというのは絶対値と言うか、ノルムみたいなものです。
皆さんは虹を見たことがありますか?見たことがない人はあまりいないと思います。
あの虹は波長(周波数)ごとに屈折率が違うために、大気の中で何らかの屈折しやすい物にぶつかった時に
それぞれの光に別れることを言います。これが光のスペクトルですが、波を分けた場合は波のスペクトルです。
一つの波をいっぱいの複素数に分けたもの、これすなわちスペクトルであります。
このスペクトルには色々使いみちがあります。
何故なら、フーリエ変換すればそれぞれの波長について、その
[波長, 位相, 振幅]が分かるからです。(波長が分かるのは自明、後の2つはさっきの式から)
応用:パワースペクトル
上記rの2乗は高校物理によるとエネルギーに比例するのは自明です。
(物理屋さんにブチ殺される発言)
つまり、rの二乗を求めさえすればその波のエネルギー的なやつを計算できます。
そうやって、波全体のパワーを周波数ごとに計算したものが
パワースペクトル密度(PSD)と言われるやつです。
応用:クロススペクトル
他の波との関係性を計算したい場合は、
それぞれのスペクトルを掛け算してあげればいいです。
この時、位相を逆にして掛け算してあげると位相の差が出たりします。
Wavelet変換とは
前置きが長かったですね。でも、まだ前置きが続きます。
窓フーリエは元の波を時間ごとに区切って有限の波の解析をしていました。
ですが、これでは「時間ごとの波の解析」の粒度が凄く低くなります。
波は移ろいゆくものですから、出来れば瞬間ごとの波の性質をみたいですよね?
何が悪いのか?
そもそも、sinやcosが無限に続く波であるのが悪いのです。
フーリエ変換に使うsinやcosを有限の波にしてやればいいんです。
大雑把に言うと
「短い波を掛け算する事で時間ごとの周波数を見ていけるんだぜ!」
的なものです。
さて、フーリエ変換の前提として全ての周波数は互いに直交
(掛け算をすると0になる。要するに無関係。)というのがありますが、
wavelet変換にもそのような前提があります。
ここからWaveletの歴史が始まります。
微分不可能なWavelet
20世紀初頭にAlfréd Haar先生という数学者がHaar Waveletというのを発明しました。
直交な関数…の中で一番単純なのはこれです。
以下をご覧ください。
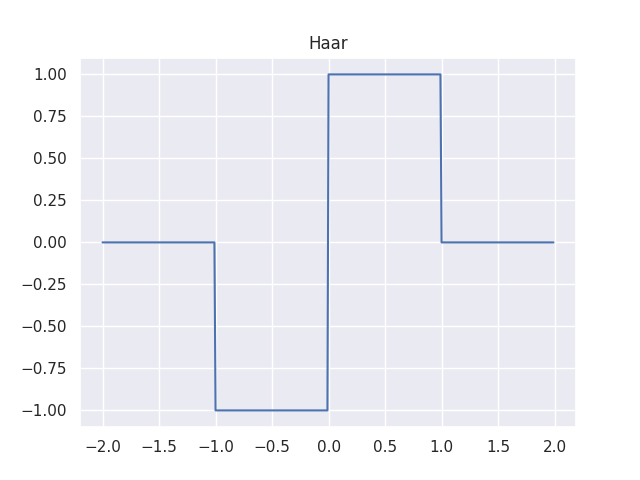
全然sinやcosと似てないじゃないか!複素数ですら無いじゃないか!
とお思いでしょう。カクカクしています。
しかし、こいつは紛れもなく小さな波であり、無難に楽にWavelet変換をすることが出来るのであります。
自然界の波の解析には向かないことも多いけれど、もちろん、HaarにはHaarの良さ1があるのです。
ちなみに、Haarの場合は畳み込みとかより速いアルゴリズムがあります。
GaborWaveletの誕生
HaarのWaveletはめっちゃカクカクしています。
でも、実際の所、自然界の波ってそんなにカクカクしていますか?そうでもないですよね。
そこでDenis Gaborという人がGaborWaveletという原始的なWaveletを考え出しました。
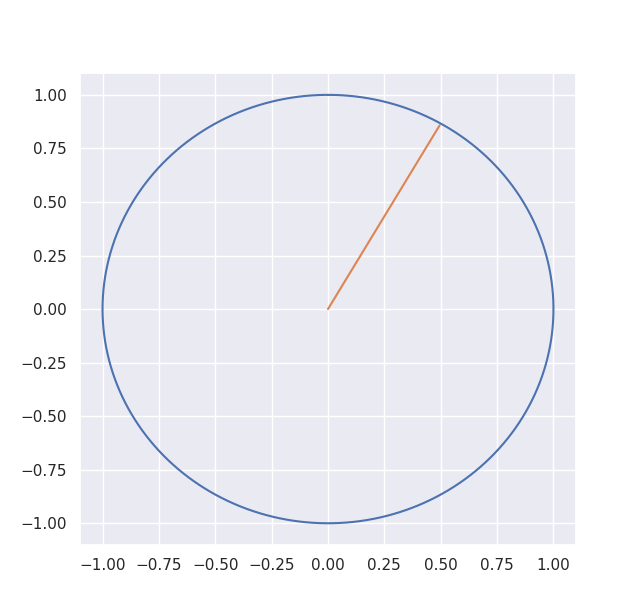
まずは、以下のWaveletの式と図をご覧ください。
$$\Psi(t) = c\sigma \pi^{\frac{-1}{4}}e^{\frac{-1}{2}t^2}e^{i\sigma t}$$
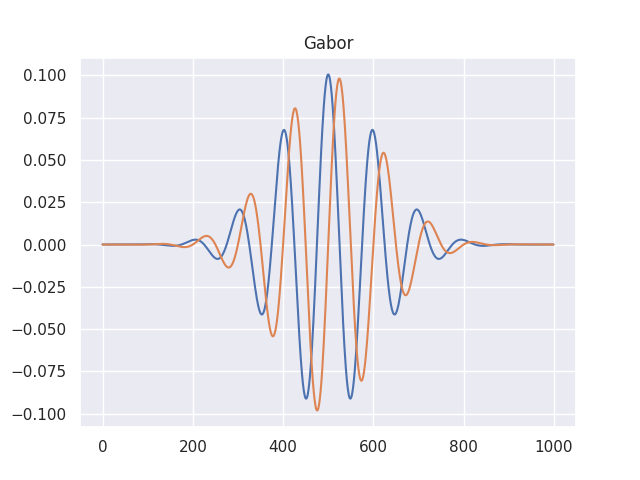
青が実軸、橙が虚軸です。
そう、ガウシアンな関数をオイラーの公式に畳み込んだやつです。
シンプルでわかりやすく、一見するととても美しい式ですね!✨
…これをMorlet waveletと解説している記事はそれなりにあります。
そのように解説している論文もあります。実際、条件によっては大差ありません。
しかし、初心者のために敢えて言います。
初心者はMorlet Waveletではなく、MorletWaveletの先祖と思いましょう
このWaveletモドキは実は条件によっては実用面では遜色ないのですが、
一つの大きな問題をはらんでいます。この波は波の長さを変えた時に常に一定になってくれないそうです。
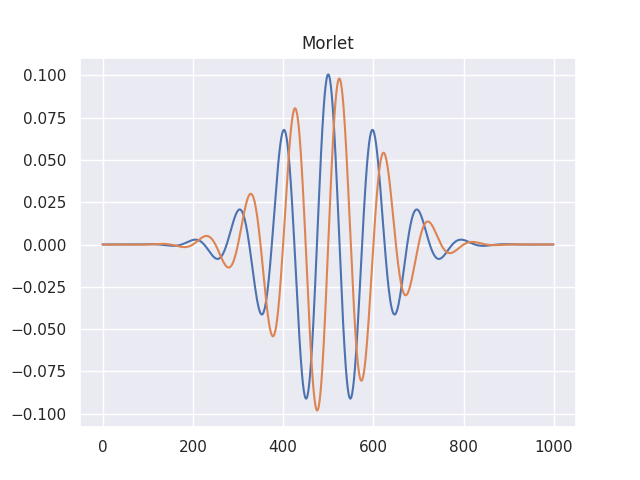
MorletWaveletとは
1980年台に、これを憂いた人たちが手を加えたそうです。
$$\Psi(t) = c\sigma \pi^{-\frac{1}{4}}e^{\frac{-1}{2}t^2}(e^{i\sigma t}-\kappa \sigma)$$
括弧の中に引き算が入りました。2
でも、これ、図は綺麗でも式の見た目的に凄く気持ち悪いですよね?
実際に$\sigma$を小さい値にしてみるとガウシアンな曲線がグチャッと潰れて
実軸小さすぎで虚軸が大きすぎな実に気持ち悪い状態になります。
その結果、パラメータによっては波の真ん中よりも周辺の方が過大評価されてしまいます。
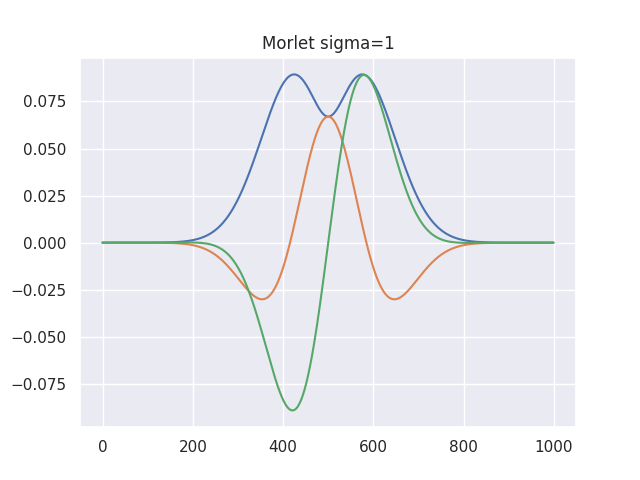
青が絶対値、橙が実軸、緑が虚軸です。
フーリエ変換に時間軸にガウシアンな関数を畳み込んで時間軸を加え、
それを正規直交基底に書き直すという自然な発想なのに、
こうなってしまっては何のためにガウシアンにしたのかさっぱりわからないですね🤔
気持ち悪さ対策
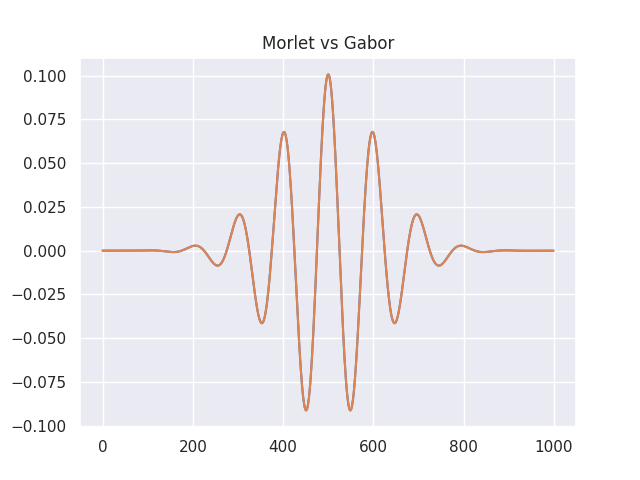
$\sigma$を大きく取ればMorletWaveletとGaborWaveletは近似され、ほぼ重なります。
下のプロットを見ても明らかでしょう。
時間解像度を犠牲にすれば全然問題ないね!
実際、僕も$\sigma=7$のMorletWaveletを愛用しており、実用上全く問題ないです。
良かったね!解散!
↓$\sigma$が7のGaborとMorletの比較。
…でも、根本的な解決になっていませんね。
そもそも$\sigma$が小さい場合はどうすれば良いのでしょうか…。
この場合は我慢してMorletWaveletを使うか、そうでなければ別のガウシアンに依存しない
Waveletを用いるところだと思います。
この世には他にも色々なWaveletがあります。
フーリエ逆変換を使って算出するWavelet
実は、フーリエ逆変換すると算出されるWaveletというのが数種類発見されています。
なんて変態的な導出の仕方なんでしょう!と思います。
これらの利点は挙げろと言われると難しいのですが、
Morletと比べて真ん中が凹まないやつが発見されていますから、そこが利点かも?
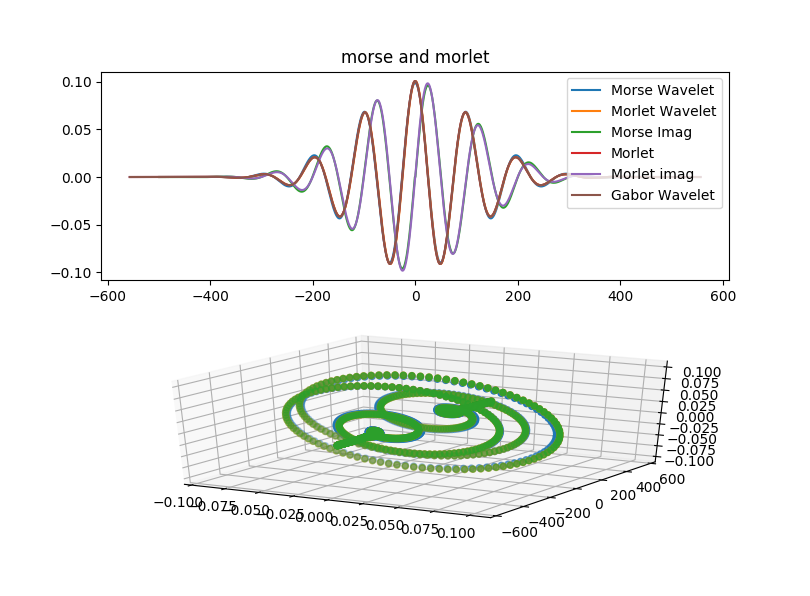
例えば2000年に入ってから知られるようになった一般モールスWavelet3というWaveletがあります。
(Morseはモールスっていう読み方で正しいのかどうかは分からないので詳しい人教えて下さい)
既にこれを脳波解析に応用している論文もあります。定義は
$$\hat{\Psi}(w) = sign(\omega) \alpha_{\beta\gamma}\omega^\beta e^{-\omega^\gamma}$$
という式…ではなく、これのフーリエ逆変換が一般モールスWaveletです。
計算上はFFTやるならフーリエ変換の手間が省けてお得ですね!
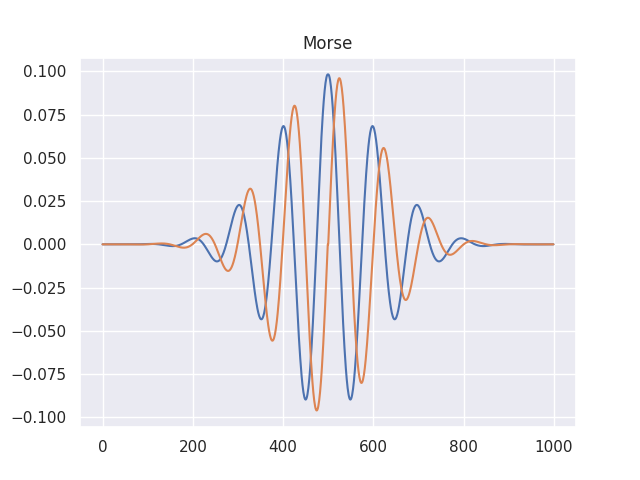
MorletWaveletとそっくりです。(パラメータいじって似せました)
ちなみに、このwaveletは$\beta$と$\gamma$で調整するんですが、
$\beta$が低かったらちびまる子ちゃんの永沢君みたいに
真ん中が尖った波になります。
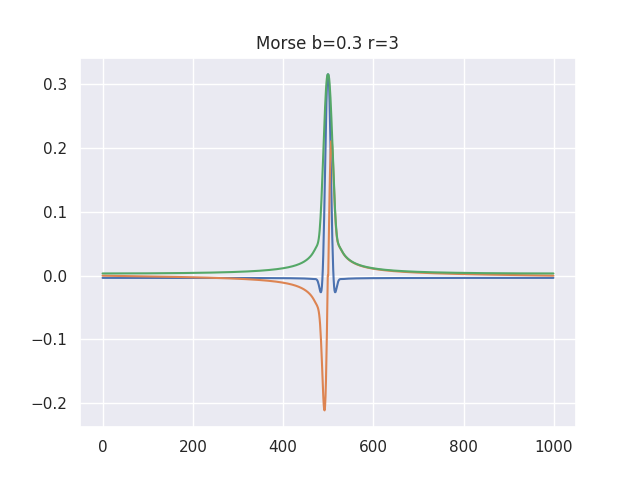
永沢君みたいなwaveletが欲しかった人には朗報なんですかね?
(周波数解像度は超絶悪くなります)
俺のWaveletパッケージ
いかがだったでしょうか?(←一度やってみたかった)
さて、上記のWaveletは検索してもpythonパッケージを見つけられませんでした。
(探し方が悪かった?)
matlabの世界にはあるんですが、ぼくそんなにお金持ちじゃない…
というわけで、MorseWaveletをpythonで実装してみました。(←こういう宣伝もやってみたかった)
https://github.com/uesseu/ninwavelets
インストールは以下で出来ます。
pip install git+ https://github.com/uesseu/ninwavelets
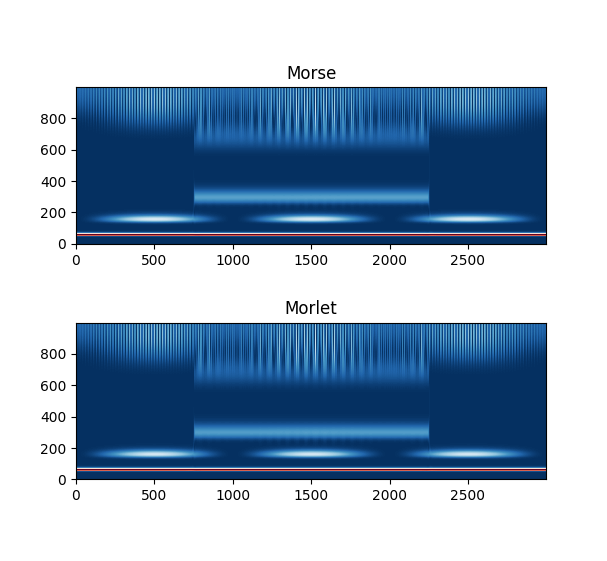
上記のHaar以外は全部このパッケージで出力しました。
下記はそのコードが吐いた図です。
いや、ほんとGaborとMorletとGMW、条件が合えばそっくりですね…
まだ か な り 若いリポジトリなので、多分色んなバグはありますし、
今後破壊的な変更もありえますが、これで一旦は
4の倍数のサンプリング周波数の波ならCWTまでは出来ます。4
令和元年8月18日追記 ちゃんと動くのを確認しました!
mne-pythonのEpochsを食べさせる事も出来ます。えらいっ!
こんなパッケージ作りにマジになっちゃってどうするの👨 完
追記
実際使えるのかどうか(令和元年8月18日)
「実際に脳波解析に使ってみたのか?あ?💢」
とかいうこわーい人が居たらしいので僕のα波をうpしますね。
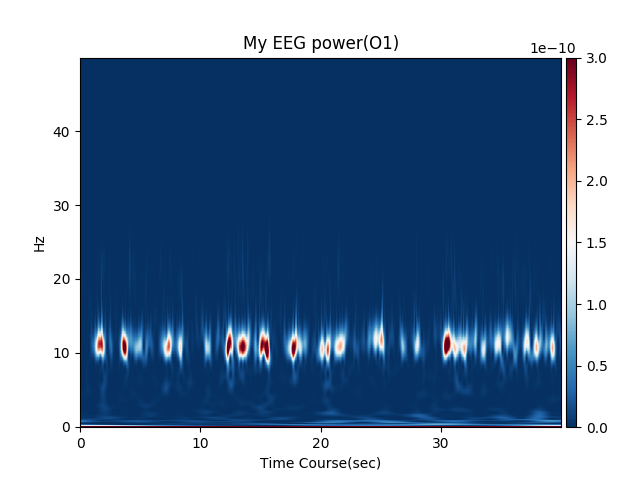
ノルムが合わない(令和元年9月9日追記)
このパッケージの問題点の一つにノルムがWaveletによって
変わってしまう問題があります。
解決方法模索中です。
(令和元年11月3日追記)
先月解決してます。その代わり、MNEpythonの結果とノルムが異なります。
まぁ、所詮趣味だし、どうでも良いわな。
これを使ってはいけない件について(令和2年5月21日)
「pythonでのGMWは実装して公開して、検証しないといけない。それは君の能力を超えている。」と言われました。
実装と公開は、まぁ、どう見てもしていますが、検証は能力を超えていると思われます。
一応リポジトリにもそう書いていますが、使ってはいけませんよ。
超高速化した(令和2年8月22日)
パッケージから無駄を取り除いたら、超高速化したのです。
だいたい、既存のパッケージの20倍位速い。
色々あって一旦非公開にした(令和2年8月31日)
ちょっと色々あるので、一旦非公開にします。
数ヶ月以内にまた公開するかと思います…。
-
計算コストとか、アルゴリズムのシンプルさとか。そもそも、用途が違うんですよね。 ↩
-
John Ashmead (2012). "Morlet Wavelets in Quantum Mechanics". Quanta. 1 (1): 58–70. arXiv:1001.0250. doi:10.12743/quanta.v1i1.5. ↩
-
Olhede, S. C., and A. T. Walden. “Generalized morse wavelets.” IEEE Transactions on Signal Processing, Vol. 50, No. 11, 2002, pp. 2661-2670. ↩
-
糞仕様なのでそのうち取り除きたい ↩