先日、つれづれなるままに
時系列分析の勉強法の記事『統計初心者が時系列分析を学ぶための勉強法』
を書き殴ってみたところ、反響の大きさに驚きました。
正直、時系列分析なんてかなりニッチな分野だ(3人ぐらいしか読まないだろう)と思ってたからです。
ステイホームしているみなさんが、暇だから時系列分析を使ってFXで一儲けしようとでも考えているんでしょうか。
時系列分析のトピックである、状態空間モデルも統計モデリングの一種なわけですが、本日は、「統計モデリングとは何なのか」について、あらためて考えてみたいと思います。
統計モデリングといえば、みんな大好き緑本『データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)』です。
緑本はたしかに素晴らしい本ですが、緑本を読んだだけでは、「何が統計モデリングで、何が統計モデリングではないのか」「統計学におけるモデルとはなにか」という私の長年の疑問は晴れませんでした。
その他、下記のような素晴らしい記事もたくさん読みましたが、書いてあることが難しく、玄人向けの説明に感じてしまいます。
ここでは、もう少し簡単なところから話をはじめ、「結局、統計モデリングとは何なのか」といった深淵な問いに迫ってみましょう。
統計モデリング力を鍛えるための勉強法については、『統計初心者が統計モデリング力を鍛えるための勉強法』も是非参考にしてみてください。
この記事の対象者
この記事は、「統計学とは」「統計学でいうところのモデルとは」「統計学と機械学習の違いとは」といった取るに足らない疑問に、ただでさえ取るに足らない人生を浪費したことのあるみなさんが対象です。
統計学の知識はほとんどなくても、理解可能な内容になっています。
それではさっそく始めましょう!
統計モデリングとはなにか
統計モデリングの基本パーツは確率分布である
統計モデリングを語る上で欠かせないのは、確率分布です。
確率分布というと、読者のみなさんは、正規分布、二項分布、ポアソン分布、ガンマ分布……etc といったものを思い浮かべるでしょう。
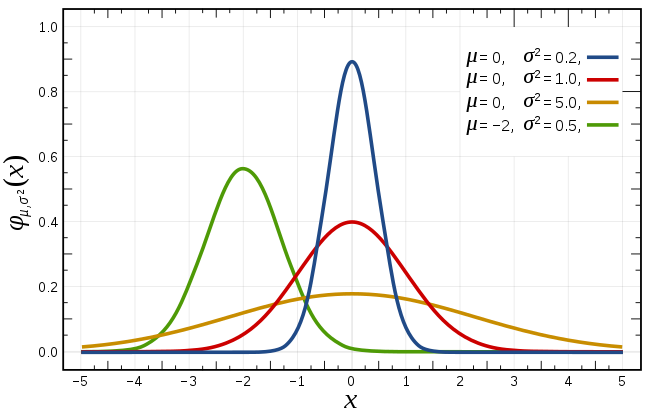
(確率分布界の皇帝として君臨している正規分布様の神々しい御姿……)
これら確率分布の数学的な性質について学ぶが統計学だと思っている方も多いようです。
それは、大学などの統計学のカリキュラムが、これら代表的な確率分布に関する数学理論から始まるためでしょう。
(だから、統計学をクソつまらないものだと思っている人が多いのでしょう。)
ですが、確率分布に関する数学理論など、統計学の本質でもなんでもありません。
重要なのは、「統計学では、確率分布を使ってどのようにモデリングをおこなうのか」です。
この記事では、「何が統計モデリングで、何が統計モデリングではないのか」を明らかにすることで、
「統計学では、確率分布を使ってどのようにモデリングをおこなうのか」。つまり、「統計モデリングとはなにか」という問いに迫っていきます。
では、これから、いくつかの質問を通して、「何が統計モデリングで、何が統計モデリングではないのか」ということを明らかにしていきましょう。
何が統計モデリングで、何が統計モデリングではないのか
Q1. 日本の全中学生男子の身長のデータがあります。これらの平均や分散を求めることは、統計モデリングと言えるでしょうか。
A1. 私の考えでは、ただ、平均や分散を計算するだけでは、統計モデリングとはいえません。
なぜなら、平均や分散は、得られたデータからそのまま計算することができるからです。
全中学生男子の身長データが手元にあるのなら、それを全部足して人数で割れば、平均を計算できます。
平均を計算できれば、分散も計算可能です。
たしかに、平均や分散を統計量といいます。
平均という概念自体が、統計学的な世界観で重要視される指標であり、
平均を求めることは、統計学的な営みだと言うこともできるかもしれません。
ですが、「モデリング」しているとは言えないと思います。
では、
Q2. 日本の全中学生男子の身長のデータに対して、どんな操作をすれば統計「モデリング」と呼べるようになるでしょうか
A2. 観測データのヒストグラムの形が正規分布っぽい?と考え、ヒストグラムに正規分布を重ねあわせたら統計モデリングの世界に一歩足を踏み入れています
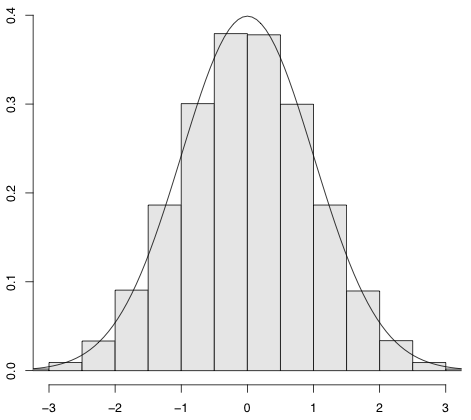
どうやら、全中学生男子の身長の分布は、正規分布に近似できるのではないか。
そう考えたあなたは、統計モデリングをはじめています。
正規分布
\frac {1}{\sqrt{2\pi\sigma^2}} \exp(-\frac {(x-\mu)^2}{2\sigma^2})\\
\\
\mu: 平均\\
\sigma^2: 分散
の平均と分散に、観測データの平均と分散を当てはめれば、上記の図のようにヒストグラムの上に正規分布をきれいに重ね合わせることができます。
得られたデータの確率分布を考える。
この観測データは、正規分布から生み出されているのではないかと考える。
それはもう立派な「統計モデリング」です。
でも、これだけで「統計モデリング」を名乗ったところで、あまり有意義なことをしたようには思えませんね。
Q3. では、統計モデリングはどんな場面で使うと意味があるのでしょうか?
A3. 一部の中学生男子の身長のデータしか手に入らない中で、全中学生男子の身長の平均や分散を推測するとき
これまでは、全中学生男子の身長が得られたことを前提にしてきましたが、実際のデータ分析の現場ではそんな幸運なことは滅多にありません。
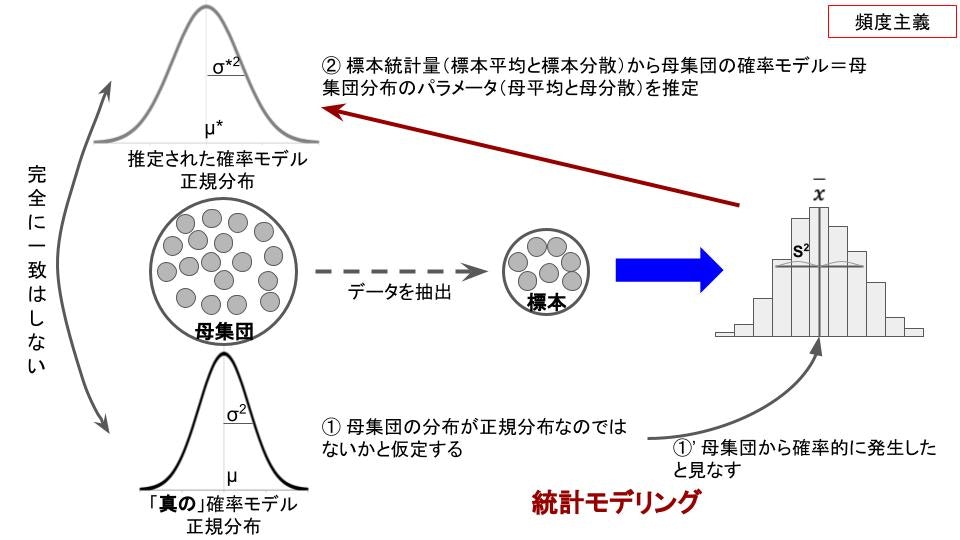
私たちには、全体のうちのごく一部のデータ(標本、サンプル)から、全体(母集団)の平均や分散の値(ベイズ統計学なら分布)について想いを巡らせるという高度に知的な営みが要求されます。
それこそが、統計学で行いたいことです。
手元のデータから母集団について想いを巡らせるためには、まず母集団の分布を仮定する必要があります。
ここでは、手元のデータしかヒントがない中で、母集団の分布を仮定する必要があります。
あなたは、これまでの経験や知識を総動員し、最も妥当だと思う確率分布(正規分布、ポアソン分布、ガンマ分布etc...)を選ぶでしょう。
ここではあなたは、母集団(=日本の全中学生男子の身長のデータ)の分布を正規分布だと仮定することになる、という流れです。
これこそが、統計モデリングです。
そして、ここが統計学の難しいところでもあります。
なぜその統計モデリングを行ったのかは、あなたの主観が入り込むとこでもあります。
そして、あなたの統計モデリングに納得するするかどうかは、あなたの主張を聞く人の主観が入ります。
ここではこれ以上の深入りはしませんが、「モデリング」の世界には、多くの場合、完全な客観だけでは判断できない余地が残ります。
一旦、統計モデリングができたら、手元にある100人の身長データは、正規分布する母集団(= 全中学生男子の身長)から生み出されたのだと考え、手元のデータから母集団の正規分布の形を想像しようとします。
正規分布の形は平均と分散がわかれば決まることが知られているので、母集団の正規分布の形を推定する問題は、母集団の平均と分散を推定する問題に置き換えられます。
これこそが、統計モデリングに基づく『統計学』的推定です。
ここでは詳しく説明しませんが、
母集団である全中学生男子の身長の平均値は、手元にある100人の身長の平均値で推定するのが、統計学的には最もリーズナブルな推定になります。
直感的には、納得感がありますよね。
母集団の分散を手元のデータから推定する計算方法は、少しややこしいので、興味のある方はご自身で勉強してみてください。
母集団の正規分布の平均と分散が推定されれば、今回の100人のデータがどの程度の確率で生み出されたものなのか(どの程度珍しいものなのか)がわかります。
それはつまり、確率論的に手元のデータを説明する手段を得たということです。
統計学と確率論は切っても切れない関係にあります。
なぜなら、統計学とは、得られたデータの生起確率を統計モデリングによって扱う学問でもあるからです。
このように統計モデリングすることができたみなさんなら、次は、どのような問題に興味が湧くでしょうか。
例えば、他の集団(日本の中学生女子や高校生男子)のデータと比較してみたいと思うかもしれません。
他の集団との比較で活躍する分析手法が、「検定」と呼ばれるものです。
検定も、母集団の確率分布を仮定することで可能になる統計学的手法です。
このように、現実世界を「統計モデリング」をすることで、その先に豊かな世界が広がっています。
その世界を統計学と呼ぶのです。
一般化線形モデルなどの回帰モデルとここで説明した統計モデリングの関係
結論から言えば、多くの方が統計モデリングと言われて思い浮かべる、
線形モデル(LM)、一般化線形モデル(GLM)、一般化線形混合モデル(GLMM)
といった統計モデルは、ここで説明した統計モデリングを回帰の世界に拡張したに過ぎません。
これらの発展的モデルも、基本パーツは、あくまで確率分布です。
例えば、冒頭でもあげた緑本や 「統計モデリングとは何なのか」をいま一度整理してみると言った記事では、主に回帰モデルを扱っています。
ですが、
真の分布を仮定して、そのパラメータの値(平均や分散。ベイズ統計学なら平均や分散自体も値ではなく分布)を手元のデータを用いて推測する
という統計モデリングの本質は、何ら変わりません。
まとめ
本日は、「結局、統計モデリングとは何なのか」という問いについて考えてみました。
統計学の本はたくさん読んできましたが、
統計学におけるモデルの意味についてここまでくどくどと説明してくれてる本はありませんでした。
特に、ここで取り上げた「何が統計モデリングで、何が統計モデリングではないのか」ということがよく分かりませんでした。
そこで、自分の考えをまとめてみようと思ったのが、この記事を書いたきっかけです。
本記事が、「統計学」という深淵な学問に挑むみなさまの参考になることを願います。
私的参考資料
最後になりますが、私が公開している下記のスライドや勉強会のアーカイブ動画でも簡単に説明しています。