はじめに
競技プログラミングではしばしばグラフ理論の問題が出題されますが、グラフ理論は Fortran にとって苦手な問題です。理由として、 Fortran には可変長配列 (他の言語では list や slice と呼ばれているもの) が実装されていないため、隣接リストを作ることができないからです。
これまで私がグラフ理論の問題に出くわした際は、 Go や Java など他の言語に逃げていましたが、 Fortran で解けないのも悔しいので Fortran で隣接リストを実装しました。またグラフ理論で登場するアルゴリズムとして Dijkstra 法、 Bellman-Ford 法、 Ford-Fulkerson 法を実装しました。
本記事では、まず始めに Fortran で可変長配列を実装し、それを用いて隣接リストを作成し、グラフ理論の問題を解くまでの流れを説明します。
module 全体のソースコードはこちらに置いておきます。
可変長配列の実装
可変長配列は以前にも実装していますが、前回はソースコードの中身の説明をしていなかったので、今回は順を追って説明します。可変長配列の実装を行なっているのは以下の部分です。
type edge
integer :: fm = 0, to = 0, cp = 0, rv = 0
integer(8) :: wt = 0_8
end type
type arraylist
integer :: num = 0
type(edge), pointer :: arr(:) => null()
contains
procedure :: add => adde
procedure :: bellman_ford => bellman_ford
end type
function newe(to,wt,fm,cp,rv) result(ret)
integer, intent(in) :: to
integer(8), intent(in) :: wt
integer, intent(in), optional :: fm, cp, rv
type(edge) :: ret
if (present(fm)) ret%fm = fm
ret%to = to
ret%wt = wt
if (present(cp) .and. present(rv)) then
ret%cp = cp
ret%rv = rv
end if
end
subroutine appende(a)
type(edge), pointer, intent(inout) :: a(:)
integer :: n
type(edge), allocatable :: tmp(:)
n = size(a)
allocate(tmp(n))
tmp = a
deallocate(a)
allocate(a(2*n))
a(1:n) = tmp
deallocate(tmp)
end
function lesse(a,b) result(ret)
type(edge), intent(in) :: a, b
logical :: ret
ret = a%wt < b%wt
end
subroutine finalizee(list)
type(arraylist), intent(inout) :: list
if (associated(list%arr)) deallocate(list%arr)
list%num = 0
end
subroutine adde(list,e)
class(arraylist), intent(inout) :: list
type(edge), intent(in) :: e
if (.not.associated(list%arr)) allocate(list%arr(1))
if (list%num == size(list%arr)) call appende(list%arr)
list%num = list%num+1
list%arr(list%num) = e
end
type(edge)
可変長配列は array list で実装しています。可変長配列が保持する要素の型は、グラフの頂点と頂点を結ぶ辺を表す type(edge) です。 type(edge) が持つフィールド変数は fm 、 to 、 cp 、 rv 、 wt の 5 つで、 fm 、 to 、 wt はその辺が頂点 fm から頂点 to を指し、重みが wt であるという情報を保持します。 cp と rv は Ford-Fulkerson 法で用いるフィールド変数で、それぞれ辺の容量と逆辺の隣接リスト上のインデックスの情報を保持します。
newe()
newe() はコンストラクタに相当する function です。引数のうち、 fm 、 cp 、 rv が optional になっていますが、これは今回作成した module では fm は Bellman-Ford 法、 cp 、 rv は Ford-Fulkerson 法でしか用いないからです。
appende()
appende() は配列の長さを伸ばす subroutine であり、 array list の実装の肝です。 array list は内部的には普通の配列と同じです。ある程度の長さの配列を用意し、その配列に要素を入れたり、配列から要素を取り出したりすることで array list の機能を果たしています。ここで問題となるのは、配列の長さよりも多くの要素を配列に追加する場合です。この場合は配列の長さを伸ばすことで解決します。 Fortran には動的割付が存在するので、 allocatable 属性か pointer 属性の付いた配列ならば配列の長さを伸ばすことが可能です。今回作成した module では、 type(arraylist) のフィールド変数である arr には pointer 属性が付いているので、長さを伸ばすことができます。
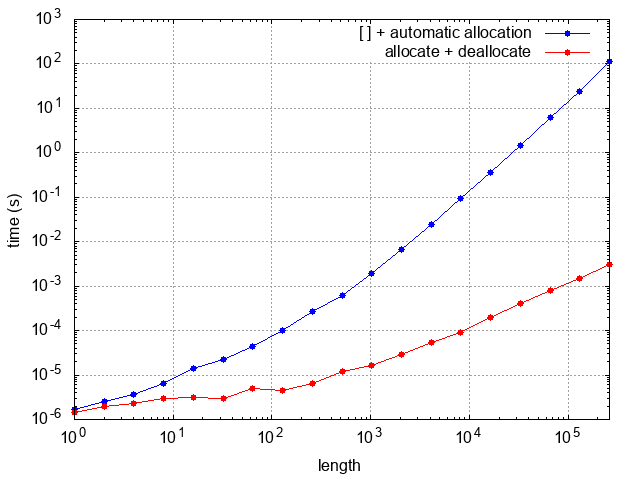
配列の長さを伸ばす方法としては、配列構成子 [] と自動割付を利用する方法と、 allocate() と deallocate() を繰り返す方法の 2 通り考えられます。配列を伸ばす操作は元の長さを $L$ とすると $O(L)$ の時間がかかります。前者の方法では要素を追加するたびに配列の長さを 1 ずつ伸ばすことになるので、 $N$ 個の要素を追加するのに $O(N^2)$ の時間がかかってしまいます。そこで後者の方法で、追加する要素数が配列の長さを超える場合は、配列の長さを 2 倍にするという戦法を取ることにより、 $O(N)$ に抑えることが可能です。
一応こちらのコードで配列の長さを伸ばすのにかかる時間を計測し、検証してみました。グラフを見てみると確かに前者の方法では $O(N^2)$ の時間がかかるのに対し、後者の方法では $O(N)$ の時間に抑えられていることがわかります。
lesse(), finalizee(), adde()
lesse() は type(edge) の comparator にあたる function 、 finalizee() は配列の要素を全て捨てる subroutine 、 adde() は配列の末尾に要素を追加する subroutine です。 lesse() は最小全域木を求める際に使うことを想定していましたが、今回は実装していません。
隣接リストの実装
可変長配列の実装ができれば、隣接リストの実装は簡単です。隣接リストは単純にグラフの頂点数の長さを持つ、可変長配列の配列で実装できます。隣接リストの実装を行なっているのは以下の部分です。
type graph
type(arraylist), pointer :: egs(:) => null()
logical, pointer :: used(:) => null()
contains
procedure :: add => add
procedure :: dijkstra => dijkstra
procedure :: ford_fulkerson => ford_fulkerson
end type
interface graph
module procedure :: newg
end interface graph
function newg(n) result(ret)
integer, intent(in) :: n
type(graph) :: ret
allocate(ret%egs(n))
end
subroutine add(g,fm,to,wt,cp)
class(graph), intent(inout) :: g
integer, intent(in) :: fm, to
integer, intent(in), optional :: cp
integer(8) :: wt
if (present(cp)) then
call adde(g%egs(fm),newe(to,wt,cp=cp,rv=g%egs(to)%num))
call adde(g%egs(to),newe(fm,wt,cp=0,rv=g%egs(fm)%num-1))
else
call adde(g%egs(fm),newe(to,wt))
end if
end
type(graph)
type(graph) のフィールド変数は egs と used です。 egs が隣接リストの部分で、 used は DFS を行う際に用いる頂点を訪ねたかどうかを記憶するための配列です。
interface graph, newg()
newg() はコンストラクタに相当する function で、グラフの頂点数を引数にとります。 interface graph はコンストラクタを type の名前で利用できるようにするために書いています。
add()
add() は隣接リストに辺を追加する subroutine です。引数は type(edge) 、 newe() の説明とほぼ同じです。
各種アルゴリズムの実装
隣接リストが実装できれば、あとは各種アルゴリズムを実装するだけです。今回実装したのは Dijkstra 法、 Bellman-Ford 法、 Ford-Fulkerson 法です。それぞれの解説は省略します。その代わり私が参考にしたサイトのリンクを下に置いておきます。
おわりに
AtCoder でグラフ理論の問題が出題されたときに、他の方の提出を見ても Fortran での提出がなかったので、他の Fortran 使いの競プロ er さんに役立てられれば幸いです。
最後に、この module を用いて解いた問題を載せておきます。
SoundHound Inc. Programming Contest 2018 -Masters Tournament-: D - Saving Snuuk
AtCoder Beginner Contest 137: E - Coins Respawn
AtCoder Grand Contest 032: C - Three Circuits
参考
Dijkstra 法: ダイクストラ法 - Wikipedia
Bellman-Ford 法: AtCoder Beginner Contest 137 解説放送 - YouTube (1:27:00 あたりから)
Ford-Fulkerson 法: フォード-ファルカーソン - きままにものづくり