Qiskitで任意の確率分布を再現する

*以下の内容はYouTubeでも一部解説しました、よかったらそちらもご覧ください。

確率分布の表現

量子コンピュータを使うと各状態(|00>や|11>など)の出現確率を出せますよね。
これを確率分布として見ることができます。うまいこと量子状態を作ると正規分布や対数正規分布なども表現することができます。
量子状態で確率分布を表現できると、量子回路で確率分布を使った期待値計算(量子モンテカルロ積分)に応用が期待されます。
例えば将来の株価の確率分布を使ってOptionなどの金融商品の計算に応用できると提案されています(ref1, ref2)。

問題はその状態の作り方です。
例えば|001>、|010>、|100>が1/3の確率で出現する分布を作りたいときにはどうしたらいいでしょうか？

この問いに答える論文がデータベース探索アルゴリズムで有名なGroverさんによって示されているので紹介します。
Creating superpositions that correspond to efficiently integrable probability distributions
2002年の論文ですが、最近の論文(前述のref1, ref2)でも引用されています。

再現する確率分布(対数正規分布)：
量子コンピュータ上でどのように確率分布を再現するのか？

Qiskit Finance Tutorialで使われている、将来T日後の株価$x$の確率分布$f(x)$を表す対数正規分布を例に解説していきます。
対数正規分布は次の式で表されます。

$$f(x) = \frac{1}{x \sigma\sqrt{2\pi}} \exp\left(-\frac{(\log x -\mu)^2}{2\sigma^2}\right)$$

ここでの$\mu$と$\sigma$はこの確率分布の平均と標準偏差で、株価の分布ではBlack-Scholesによると

\begin{eqnarray}
 \mu &=&(r-\sigma^2/2)T+\ln{S_0}\\
 \sigma &=& \sigma_v\sqrt{T}
\end{eqnarray}

と表されます。平均$\mu$と標準偏差$\sigma$を表すのに使った定数はQiskit Finance Tutorialでは次のように設定されています。

現時点の株価 $S_0$	ボラリティリティ $\sigma_v$	年利 $r$	予測対象日 $T$
\$2.0	0.4	0.05	40/364 (40日後)

import numpy as np
# parameters for considered random distribution
S = 2.0       # initial spot price
vol = 0.4     # volatility of 40%
r = 0.05      # annual interest rate of 4%
T = 40 / 365  # 40 days to maturity

# resulting parameters for log-normal distribution
mu = ((r - 0.5 * vol**2) * T + np.log(S))
sigma = vol * np.sqrt(T)
mean = np.exp(mu + sigma**2/2)

print(f"mu: {mu}")
print(f"sigma: {sigma}")

mu: 0.6898595093270685
sigma: 0.13241694217637887

目標は、量子ビットでのこの確率分布を再現することです。ここでは、左の図のように３量子ビットで再現を試みます。横軸は株価$x$ですが左から000, 001, ..., 111と読み替えます。量子での分布は離散化しているので、欲しい範囲で打ち切りし、量子ビット数nに対してヒストグラムのビン数が$2^n$になるように設定します。ここでそれぞれのビンが表す測定の確率を$p_{000}, p_{001},..,p_{111}$と表していきます。

この図はqiskit.circuit.library.LogNormalDistributionというモジュールを使って簡単に作ることができます。
もしくはnp.random.lognormal(mean=mu, sigma=sigma, size=N)というモジュールでサンプリングして、範囲とビン数を揃える後処理をしても大丈夫です。

左図のプロット

import matplotlib.pyplot as plt
from qiskit.circuit.library import LogNormalDistribution

# 分布を表すのに使用する量子ビット数
num_uncertainty_qubits = 3

# プロット範囲を設定
variance = (np.exp(sigma**2) - 1) * np.exp(2*mu + sigma**2)
stddev = np.sqrt(variance)
low  = np.maximum(0, mean - 3*stddev)
high = mean + 3*stddev

# 量子ビットの数に応じた離散分布の作成
uncertainty_model = LogNormalDistribution(num_uncertainty_qubits, mu=mu, sigma=sigma**2, bounds=(low, high))

# プロット
x = uncertainty_model.values
y = uncertainty_model.probabilities
plt.bar(x, y, width=0.2)
plt.xticks(x, size=15, rotation=90)
plt.yticks(np.linspace(0,0.4, 5) ,size=15)
plt.xlabel('Spot Price at Maturity $S_T$ (\$)', size=15)
plt.ylabel('Probability ($\%$)', size=15)
plt.ylim(0,0.4)
plt.show()

それでは、上図の3量子ビット表現の確率分布をどのように作成していくのかを解説します。作りたい状態は

$$\left|\psi_3\right\rangle = \sum_{i,j,k \in \{0, 1\}}\sqrt{p_{ijk}}\left|ijk\right\rangle $$
です。この状態を作るために、1量子ビット表現$\left|\psi_1\right\rangle$と2量子ビット表現$\left|\psi_2\right\rangle$を作成していきます。

\begin{eqnarray}
&\left|\psi_1\right\rangle = \sum_{i \in \\{0, 1\\}}\sqrt{p_{i}}\left|i\right\rangle \\
&\left|\psi_2\right\rangle = \sum_{i,j \in \\{0, 1\\}}\sqrt{p_{ij}}\left|ij\right\rangle
\end{eqnarray}

ここで1量子ビット表現は、確率分布を2分割に縮約した表現で、2量子ビットは表現は4分割に縮約した表現です。これらの表現に対応する確率$p_i ,p_{ij}$ は、 目的の３量子ビット表現と次のように関係しています。

$p_i$ : 3量子ビット中1個目のビットの観測値が$i$の確率
$p_{ij}$: 3量子ビット中1,2個目のビットの観測値が$ij$の確率

具体的には、$p_i, p_{ij}, p_{ijk}$の関係は次のようになります。

\begin{eqnarray}
&&p_0=p_{000}+p_{001}+p_{010}+ p_{011} \\
&&p_1=p_{100}+p_{101}+p_{110}+ p_{111} \\
\\
&&p_{00}=p_{000}+p_{001} \\
&&p_{01}=p_{010}+ p_{011} \\
&&p_{10}=p_{100}+p_{101} \\
&&p_{11}=p_{110}+ p_{111} 
\end{eqnarray}

以降は$\left|\psi_1\right\rangle$をもとに$\left|\psi_2\right\rangle$を作成し、$\left|\psi_2\right\rangle$をもとに$\left|\psi_3\right\rangle$を作成していきます。

1量子ビット表現：
確率分布を1量子ビットで再現する量子回路とは？

最初に先ほどの図を1量子ビットで表してみます(左図)。これは3量子ビットのビンを集約し、$p_0$と$p_1$で表していることになります。

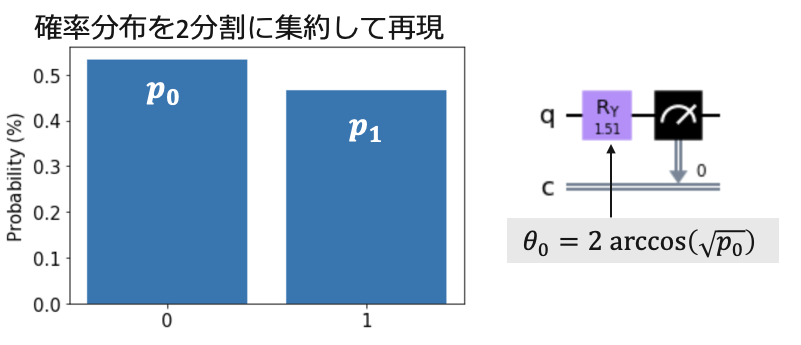
この左図の分布を量子回路で再現するには、右図のようにRYゲートを使用します。RYゲートは次のような行列に対応します。

RY_\theta = \exp\left(-i\frac{\theta}{2}Y\right)= 
\begin{pmatrix}
\cos{\frac{\theta}{2}} & -\sin{\frac{\theta}{2}} \\
\sin{\frac{\theta}{2}} & \cos{\frac{\theta}{2}} 
\end{pmatrix}

ここで$\theta$ は$\cos$の逆関数$\arccos$を使って$\theta_0 = 2 \arccos(\sqrt{p_0})$とします。こうすることで、

\begin{eqnarray}
\left|\psi_1\right\rangle &=& RY(\theta_0)|0\rangle \\
  &=& \cos{\frac{\theta_0}{2}}\left|0\right\rangle 
+ \sin{\frac{\theta_0}{2}}\left|1\right\rangle \\
&=& \sqrt{p_0}\left|0\right\rangle + \sqrt{1-p_0}\left|1\right\rangle
\end{eqnarray}

と欲しい状態が得られます。

これに対応するコードは以下のようになります。

中央図のプロット・右図の回路作成

from qiskit import Aer, QuantumRegister, QuantumCircuit, execute
from qiskit.visualization import plot_histogram
backend = Aer.get_backend('qasm_simulator')
shots=10000


def circuit_bin2(theta):
    """|ψ1>を作成"""
    qc = QuantumCircuit(1,1)
    qc.ry(theta, 0)
    qc.measure(0,0)
    return qc


# 分布を２分割に集約
p0, p1 = np.array(np.array_split(uncertainty_model.probabilities, 2)).sum(axis=1)
theta0 = 2*np.arccos(np.sqrt(p0))

# 回路作成して測定
qc =   circuit_bin2(theta0)                  
counts = execute(qc, backend,shots=shots,seed_simulator=1).result().get_counts()

# プロット 
ax1 = plt.figure(figsize=(7,3),dpi=100, facecolor="w", linewidth=0, edgecolor="w").add_subplot(1,1,1)
ax2 = plt.figure(figsize=(7,3),dpi=100, facecolor="w", linewidth=0, edgecolor="w").add_subplot(1,1,1)

plot_histogram(counts,ax=ax1)
qc.draw("mpl",ax=ax2)

2量子ビット表現：
確率分布を2量子ビットで再現する量子回路とは？

では次に1量子ビット表現$\left|\psi_1\right\rangle$から２量子ビット表現$\left|\psi_2\right\rangle$に拡張しましょう。この量子状態を作るには、1量子ビットでの場合の$\left|0\right\rangle$の係数$p_0$を$p_{00}:p_{01}$の比率で分割し$\left|00\right\rangle$と$\left|01\right\rangle$に割り当てて、$\left|1\right\rangle$の係数$p_1$を$p_{10}:p_{11}$の比率で分割し$\left|10\right\rangle$と$\left|11\right\rangle$に割り当てます。これは制御RYゲートで、1量子ビット版の拡張として下図ようにかけます。$\left|0\right\rangle, \left|1\right\rangle$に対する回転角$\theta_1, \theta_2$は以下の図のように設定します。

Xゲートに挟まれた１つ目の制御$RY(\theta_1)$は１量子ビット目が$\left|0\right\rangle$のとき、$\cos(\theta_1/2)\left|00\right\rangle+\sin(\theta_1/2)\left|01\right\rangle$の状態を生成します。
同様に2つ目の制御$RY(\theta_2)$は１量子ビット目が$\left|1\right\rangle$のとき、$\cos(\theta_2/2)\left|10\right\rangle+\sin(\theta_2/2)\left|11\right\rangle$の状態を生成します。

この時の量子状態を計算してみます。

\begin{eqnarray}
|\psi_2\rangle &=&  \sqrt{p_0}\left|0\right\rangle \left( RY(\theta_1) \left|0\right\rangle \right) 
+ \sqrt{1-p_0^2} \left|1\right\rangle (RY(\theta_2) \left|0\right\rangle) \\

&=& \sqrt{p_0}\left|0\right\rangle \left(
 \cos{\frac{\theta_1}{2}}\left|0\right\rangle + \sin{\frac{\theta_1}{2}}\left|1\right\rangle
\right)
 + \sqrt{1-p_0^2}\left|1\right\rangle  \left(
 +  \cos{\frac{\theta_2}{2}}\left|0\right\rangle + \sin{\frac{\theta_2}{2}}\left|1\right\rangle \right)\\

&=& \sqrt{p_0}\left|0\right\rangle \left(
 \sqrt{\frac{p_{00}}{p_0}}\left|0\right\rangle+ \sqrt{1-\frac{p_{00}}{p_0}}\left|1\right\rangle
\right)
  + \sqrt{p_1}\left|1\right\rangle \left(
  + \sqrt{\frac{p_{10}}{p_1}}\left|0\right\rangle + \sqrt{1-\frac{p_{10}}{p_1}}\left|1\right\rangle
  \right)\\

&=& \sqrt{p_{00}}\ \left|00\right\rangle + \sqrt{p_0-p_{00}}\ \left|01\right\rangle 
+ \sqrt{p_{10}}\ \left|10\right\rangle + \sqrt{p_1-p_{10}}\ \left|11\right\rangle  \\

&=& \sqrt{p_{00}}\ \left|00\right\rangle + \sqrt{p_{01}}\ \left|01\right\rangle 
+ \sqrt{p_{10}}\ \left|10\right\rangle + \sqrt{p_{11}}\ \left|11\right\rangle 
\end{eqnarray}

ちゃんと欲しい状態になっていますね。
こちらの回路作成とヒストグラムのプロットのコードは以下のようになります。

def circuit_bin4(theta0, theta1, theta2):
    qc = QuantumCircuit(2,2)
    qc.ry(theta0,0)
    # |0>状態にRY(theta1)を作用
    qc.x(0)
    qc.cry(theta1,0, 1)
    qc.x(0)
    # |1>状態にRY(theta2)を作用
    qc.cry(theta2,0, 1)
    qc.measure([0,1],[1,0])
    return qc

# 分布を4分割に集約
p00, p01, p10, p11 = np.array(np.array_split(uncertainty_model.probabilities, 4)).sum(axis=1)
theta1 = 2*np.arccos(np.sqrt(p00/p0))
theta2 = 2*np.arccos(np.sqrt(p10/p1))

# 回路作成して測定
qc =   circuit_bin4(theta0, theta1, theta2)                  
counts = execute(qc, backend,shots=shots,seed_simulator=1).result().get_counts()

# プロット 
ax1 = plt.figure(figsize=(7,3),dpi=100, facecolor="w", linewidth=0, edgecolor="w").add_subplot(1,1,1)
ax2 = plt.figure(figsize=(7,3),dpi=100, facecolor="w", linewidth=0, edgecolor="w").add_subplot(1,1,1)

plot_histogram(counts,ax=ax1)
qc.draw("mpl",ax=ax2)

3量子ビット表現：
確率分布を3量子ビットで再現する量子回路とは？

では最後に2量子ビットから3量子ビットに状態に拡張してみます。
このとき、次のように制御RYゲートの角度を定めます。

ではこの時の量子状態も示してみます(細かい計算は省略)。

\begin{eqnarray}
\left|\psi_3\right\rangle &=&  \sqrt{p_{00}}\left|00\right\rangle \left( RY(\theta_3) \left|0\right\rangle \right) 
+ \sqrt{p_{01}}\left|01\right\rangle \left( RY(\theta_4) \left|0\right\rangle \right) 
+ \sqrt{p_{10}}\left|10\right\rangle \left( RY(\theta_5) \left|0\right\rangle \right) 
+ \sqrt{p_{11}}\left|11\right\rangle \left( RY(\theta_6) \left|0\right\rangle \right) \\

&=& \sqrt{p_{00}}\left|00\right\rangle \left(
 \sqrt{\frac{p_{000}}{p_{00}}}\left|0\right\rangle+ \sqrt{1-\frac{p_{000}}{p_{00}}}\left|1\right\rangle
\right)
  + \sqrt{p_{01}}\left|01\right\rangle \left(
  + \sqrt{\frac{p_{010}}{p_{01}}}\left|0\right\rangle + \sqrt{1-\frac{p_{010}}{p_{01}}}\left|1\right\rangle
  \right)\\
&& \quad
 + \sqrt{p_{10}}\left|10\right\rangle \left(
 \sqrt{\frac{p_{100}}{p_{10}}}\left|0\right\rangle+ \sqrt{1-\frac{p_{100}}{p_{10}}}\left|1\right\rangle
\right)
  + \sqrt{p_{11}}\left|11\right\rangle \left(
  + \sqrt{\frac{p_{110}}{p_{11}}}\left|0\right\rangle + \sqrt{1-\frac{p_{110}}{p_{11}}}\left|1\right\rangle
  \right)\\
&=& \sqrt{p_{000}}\ \left|000\right\rangle + \sqrt{p_{001}}\ \left|001\right\rangle 
+ \sqrt{p_{010}}\ \left|010\right\rangle + \sqrt{p_{011}}\ \left|011\right\rangle  \\
&& \quad \quad
+ \sqrt{p_{100}}\ \left|100\right\rangle + \sqrt{p_{101}}\ \left|001\right\rangle 
+ \sqrt{p_{110}}\ \left|110\right\rangle + \sqrt{p_{111}}\ \left|011\right\rangle  
\end{eqnarray}

これで欲しい状態を再現することができました。
こちらもコードを貼っておきます。CCRYの実装はQiskitでRYやCRYのように書けないので、ちょっと工夫が必要です。

from qiskit.circuit.library import RYGate

def circuit_bin8(theta0, theta1, theta2, theta3, theta4, theta5, theta6):
    qc = QuantumCircuit(3,3)
    qc.ry(theta0,0)

    # |0>状態にRY(theta1)を作用
    qc.x(0)
    qc.cry(theta1,0, 1)
    qc.x(0)
    # |1>状態にRY(theta2)を作用
    qc.cry(theta2,0, 1)

    # |00>状態にRY(theta3)を作用
    qc.x([0,1])
    qc.append(RYGate(theta3).control(2), [0,1,2])
    qc.x([0,1])
    # |01>状態にRY(theta4)を作用
    qc.x(0)
    qc.append(RYGate(theta4).control(2), [0,1,2])
    qc.x(0)
    # |10>状態にRY(theta5)を作用
    qc.x(1)
    qc.append(RYGate(theta5).control(2), [0,1,2])
    qc.x(1)
    # |11>状態にRY(theta6)を作用
    qc.append(RYGate(theta6).control(2), [0,1,2])

    qc.measure([0, 1, 2],[2, 1, 0])
    return qc


# 分布を8分割に集約(オリジナルのまま)
p000, p001, p010, p011, p100, p101, p110, p111 = uncertainty_model.probabilities
theta3 = 2*np.arccos(np.sqrt(p000/p00))
theta4 = 2*np.arccos(np.sqrt(p010/p01))
theta5 = 2*np.arccos(np.sqrt(p100/p10))
theta6 = 2*np.arccos(np.sqrt(p110/p11))


# 回路作成して測定
qc =   circuit_bin8(theta0, theta1, theta2, theta3, theta4, theta5, theta6)                 
counts = execute(qc, backend,shots=shots,seed_simulator=1).result().get_counts()

# プロット 
ax1 = plt.figure(figsize=(7,3),dpi=100, facecolor="w", linewidth=0, edgecolor="w").add_subplot(1,1,1)
ax2 = plt.figure(figsize=(7,3),dpi=100, facecolor="w", linewidth=0, edgecolor="w").add_subplot(1,1,1)

plot_histogram(counts,ax=ax1)
qc.draw("mpl",ax=ax2)

ゲートコスト：
確率分布をより効率よく表現するための量子回路の工夫とは？

このようにして所望の確率分布をシステマティックに作成することができます。この方法を使えばGHZ状態$\frac{1}{\sqrt{2}}\left(\left|000\right\rangle+\left|111\right\rangle\right)$も閃きや直観を必要とせずに構成することができます。

しかし、この方法の欠点は量子ビット数が増えると必要なゲート数が指数関数的に増加することです。

Transpilerを使って上記の3つの回路で$ U_3$ゲートとCXゲートに分解してゲートの操作回数をカウントしてみます。

from qiskit.transpiler import PassManager
from qiskit.transpiler.passes import Unroller

def gate_decompose(qc):
    pass_ = Unroller(['u3', 'cx'])
    return PassManager(pass_).run(qc).count_ops()

qc_bin2 = circuit_bin2(theta0) 
print(gate_decompose(qc_bin2))
qc_bin4 = circuit_bin4(theta0, theta1, theta2)
print(gate_decompose(qc_bin4))
qc_bin8 = circuit_bin8(theta0, theta1, theta2, theta3, theta4, theta5, theta6)
print(gate_decompose(qc_bin8))

OrderedDict([('u3', 1), ('measure', 1)])
OrderedDict([('u3', 7), ('cx', 4), ('measure', 2)])
OrderedDict([('u3', 95), ('cx', 52), ('measure', 3)])

	$U_3$ゲート	CXゲート
1量子ビット回路	1	0
2量子ビット回路	7	4
3量子ビット回路	95	52

計算コストの観点では効率的とは言えないので、ゲート数を減らす方法を考えるにはやはり閃きや直観が必要になりますね。実はこの確率分布の再現の課題の解決策として、量子GANという方法が提案されました。別の記事で量子GANについて詳しく解説していきたいと思います。

コメント

この方法で任意の確率分布をこの方法で表現できるので、Qiskit Challegeなどの量子コンピュータのコンテストでは有用なテクニックになるかもしれません。

Version情報

以下の解説で使用したQiskitのVersionは次の通りです。

import qiskit
qiskit.__qiskit_version__

{'qiskit-terra': '0.16.3',
'qiskit-aer': '0.7.3',
'qiskit-ignis': '0.5.1',
'qiskit-ibmq-provider': '0.11.1',
'qiskit-aqua': '0.8.1',
'qiskit': '0.23.4'}

Acknowledgement

@ibmamntさんに、CCRYを実装する方法と1セルで量子回路とヒストグラムをプロットする方法をアドバイスいただきました。
@ryosaさんに内容に関してアドバイスいただきました。