はじめに
こんにちは。私は、とある塾で校長をやっております。
塾では、生徒たちが日々勉強を頑張っています。
黙々と一人で毎日勉強する子もいれば、忙しくてあまり塾に通えない子もいます。
そんな私が、長年答えが出なかった成績についての悩みを、プログラミングで解決しようとした経緯と結果をここに書きます。
学校や塾も含めて教育に携わっている方、少しでも興味がある方は是非一読してみてください。
きっかけ
自分の校舎の生徒の成績を上げたいと思ったからです
私は思い悩んでいました。頑張っている生徒はたくさんいるのに、全員が全員好成績を取れるわけではないのです。
少し手を抜いているように見える子よりも、勉強を日々頑張っている子の方が成績が悪いこともあるのです。
そんな子たちをなんとかできないものか…
そもそも、成績を上げるためには何が必要なのか?
そして、ふと思いつきました!💡
その未来永劫続きそうな疑問を、プログラミングで解決できないか?
思い立ったらすぐでした。
最初は独学で3か月、その後はaidemyにて6か月。みっちりと学習して最初の成果物としてこの記事を書いています。
目標
生徒の成績向上を促進/阻害する要因を見つける
目的
1.データセットの各説明変数の中から、生徒の成績が上がる/下がる原因を特定する
2.成績が上がった/下がった生徒に対して、精度の高い成績予測のモデルを作成する
ざっくりとした手順
1.データのinput
2.データの修正
3.成績ごとに各説明変数の相関性を確認
4.成績が上がる/下がる原因の推測
5.データを削減/統合し、モデル化
6.校舎の生徒の成績向上を促進/阻害する要因の推測
7.今後の展望
言語はPython、環境はKaggle Notebookを使用した。
内容
1.データのinput
今回は以下のKaggleのデータセットを使用した。
タイトル:Student Grade Prediction
URL:https://www.kaggle.com/dipam7/student-grade-prediction
【データの詳細】
ポルトガルのsecondary educationの生徒(日本でいう高校生)に対して行ったアンケートや報告書に基づいたデータセット。データ数と説明変数は以下の通り。
コードはこちら
data = pd.read_csv("/kaggle/input/student-grade-prediction/student-mat.csv")
print(data.shape)
print(data.columns)
(395, 33)
Index(['school', 'sex', 'age', 'address', 'famsize', 'Pstatus', 'Medu', 'Fedu',
'Mjob', 'Fjob', 'reason', 'guardian', 'traveltime', 'studytime',
'failures', 'schoolsup', 'famsup', 'paid', 'activities', 'nursery',
'higher', 'internet', 'romantic', 'famrel', 'freetime', 'goout', 'Dalc',
'Walc', 'health', 'absences', 'G1', 'G2', 'G3'],
dtype='object')
データ数(生徒数)は395、説明変数の数は33。
【データの確認】
コードはこちら
print(data.describe())
print(data.describe(exclude="number"))
print(data.dtypes)
結果の詳細はこちら
age Medu Fedu traveltime studytime failures \count 395.000000 395.000000 395.000000 395.000000 395.000000 395.000000 \
mean 16.696203 2.749367 2.521519 1.448101 2.035443 0.334177 \
std 1.276043 1.094735 1.088201 0.697505 0.839240 0.743651 \
min 15.000000 0.000000 0.000000 1.000000 1.000000 0.000000 \
25% 16.000000 2.000000 2.000000 1.000000 1.000000 0.000000 \
50% 17.000000 3.000000 2.000000 1.000000 2.000000 0.000000 \
75% 18.000000 4.000000 3.000000 2.000000 2.000000 0.000000 \
max 22.000000 4.000000 4.000000 4.000000 4.000000 3.000000 \
famrel freetime goout Dalc Walc health \
count 395.000000 395.000000 395.000000 395.000000 395.000000 395.000000 \
mean 3.944304 3.235443 3.108861 1.481013 2.291139 3.554430 \
std 0.896659 0.998862 1.113278 0.890741 1.287897 1.390303 \
min 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000 \
25% 4.000000 3.000000 2.000000 1.000000 1.000000 3.000000 \
50% 4.000000 3.000000 3.000000 1.000000 2.000000 4.000000 \
75% 5.000000 4.000000 4.000000 2.000000 3.000000 5.000000 \
max 5.000000 5.000000 5.000000 5.000000 5.000000 5.000000 \
absences G1 G2 G3
count 395.000000 395.000000 395.000000 395.000000
mean 5.708861 10.908861 10.713924 10.415190
std 8.003096 3.319195 3.761505 4.581443
min 0.000000 3.000000 0.000000 0.000000
25% 0.000000 8.000000 9.000000 8.000000
50% 4.000000 11.000000 11.000000 11.000000
75% 8.000000 13.000000 13.000000 14.000000
max 75.000000 19.000000 19.000000 20.000000
school sex address famsize Pstatus Mjob Fjob reason guardian \count 395 395 395 395 395 395 395 395 395 \
unique 2 2 2 2 2 5 5 4 3 \
top GP F U GT3 T other other course mother \
freq 349 208 307 281 354 141 217 145 273 \
schoolsup famsup paid activities nursery higher internet romantic
count 395 395 395 395 395 395 395 395
unique 2 2 2 2 2 2 2 2
top no yes no yes yes yes yes no
freq 344 242 214 201 314 375 329 263
school object
sex object
age int64
address object
famsize object
Pstatus object
Medu int64
Fedu int64
Mjob object
Fjob object
reason object
guardian object
traveltime int64
studytime int64
failures int64
schoolsup object
famsup object
paid object
activities object
nursery object
higher object
internet object
romantic object
famrel int64
freetime int64
goout int64
Dalc int64
Walc int64
health int64
absences int64
G1 int64
G2 int64
G3 int64
dtype: object
・欠損値がない。
・objectと数値データが混在している。
・数値以外のデータの特徴数が分かった。
以上のことが分かった。
2.データの修正
このままではモデルの作成の際に支障が出るので、objectデータを数値データに変換した。
以下の手順で行う。
① 特徴量が2のobjectデータに対し、One-Hot Encodingを施す。
② ①で変更されたカラム名を戻す
③ 特徴量が3~5のobjectデータに対し、replaceメソッドにて、数値データに変換
④ 特徴量の多い"absences"に対してカテゴリカル変数化し、数値データに変換
⑤ ①で増えてしまった不要なカラムを削除
コードはこちら
# ①
data = pd.get_dummies(data, columns=['school', 'sex', 'address', 'famsize', 'Pstatus', 'schoolsup', 'famsup', 'paid', 'activities', 'nursery', 'higher', 'internet', 'romantic'])
# ②
data = data.rename(columns={"school_GP":"school", "sex_M":"sex", "address_U":"address", "famsize_GT3":"famsize", "Pstatus_T":"Pstatus", "schoolsup_yes":"schoolsup", 'famsup_yes':"famsup", 'paid_yes':"paid", 'activities_yes':"activities", 'nursery_yes':"nursery", 'higher_yes':"higher", 'internet_yes':"internet", 'romantic_yes':"romantic"})
# ③
Mjob = ["services", "teacher", "at_home", "health", "other"]
Fjob = ["services", "teacher", "at_home", "health", "other"]
reason = ["course", "home", "reputation", "other"]
guardian = ["mother", "father", "other"]
data["Mjob"] = data["Mjob"].replace(Mjob, [1, 2, 3, 4, 5])
data["Fjob"] = data["Fjob"].replace(Fjob, [1, 2, 3, 4, 5])
data["reason"] = data["reason"].replace(reason, [1, 2, 3, 4])
data["guardian"] = data["guardian"].replace(guardian, [1, 2, 3])
# ④
data["absencesband"] = pd.qcut(data["absences"].rank(method='first'), 4, labels = [1, 2, 3, 4])
data["absencesband"] = data["absencesband"].astype(int)
# ⑤
drop_col = ['school_MS', 'sex_F', 'address_R', 'famsize_LE3', 'Pstatus_A', 'schoolsup_no', 'famsup_no', 'paid_no', 'activities_no', 'nursery_no', 'higher_no', 'internet_no', 'romantic_no', "absences"]
data.drop(drop_col, axis=1, inplace=True)
コードはこちら
data["G_s"] = data["G3"] - data["G1"]
data_high = data.query("G_s > 0").reset_index(drop=True)
data_mid = data.query("G_s == 0").reset_index(drop=True)
data_low = data.query("G_s < 0").reset_index(drop=True)
print("成績上昇:", data_high.shape)
print("成績不変:", data_mid.shape)
print("成績下降:", data_low.shape)
成績上昇: (143, 40)
成績不変: (93, 40)
成績下降: (159, 40)
となり、成績が上がったものと下がってもので約各150ずつのデータになった。
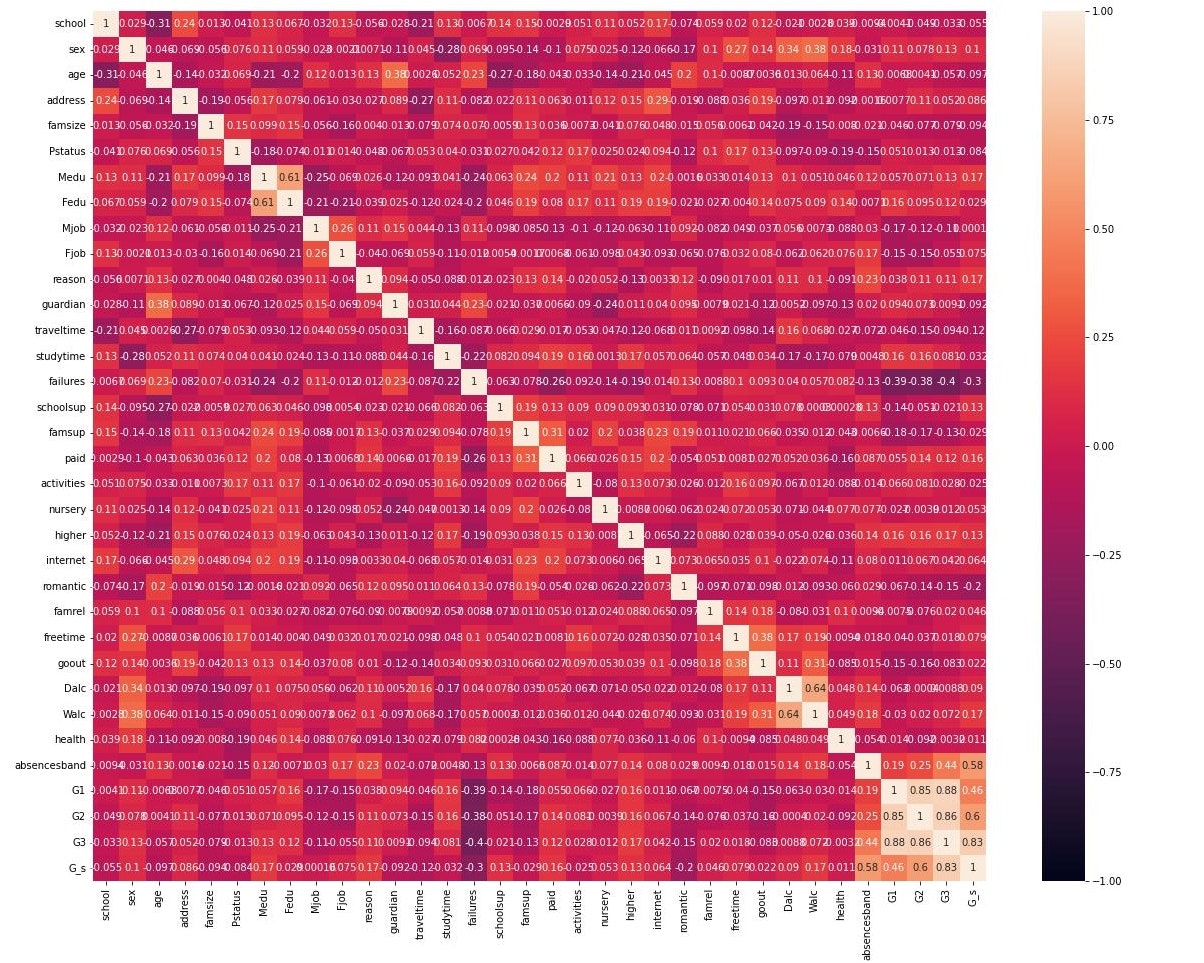
3.成績ごとに各説明変数の相関性を確認
次に、成績が上がった/下がった生徒の、各項目の相関を見ることで、成績が上がっている/下がっている要因を見つける足掛かりにしたい。
コードはこちら
import seaborn as sns
fig, ax = plt.subplots(figsize=(20, 16))
sns.heatmap(data_high[['school', 'sex', 'age', 'address', 'famsize', 'Pstatus', 'Medu', 'Fedu', 'Mjob', 'Fjob', 'reason', 'guardian', 'traveltime', 'studytime',
'failures', 'schoolsup', 'famsup', 'paid', 'activities', 'nursery', 'higher', 'internet', 'romantic', 'famrel', 'freetime', 'goout', 'Dalc', 'Walc', 'health', 'absencesband', 'G1', "G2", "G3", "G_s"]].corr(),vmax=1,vmin=-1,annot=True)
fig, ax = plt.subplots(figsize=(20, 16))
sns.heatmap(data_low[['school', 'sex', 'age', 'address', 'famsize', 'Pstatus', 'Medu', 'Fedu', 'Mjob', 'Fjob', 'reason', 'guardian', 'traveltime', 'studytime', 'failures', 'schoolsup', 'famsup', 'paid', 'activities', 'nursery', 'higher',
'internet', 'romantic', 'famrel', 'freetime', 'goout', 'Dalc', 'Walc', 'health', 'absencesband', 'G1', "G2", "G3", "G_s"]].corr(),vmax=1,vmin=-1,annot=True)
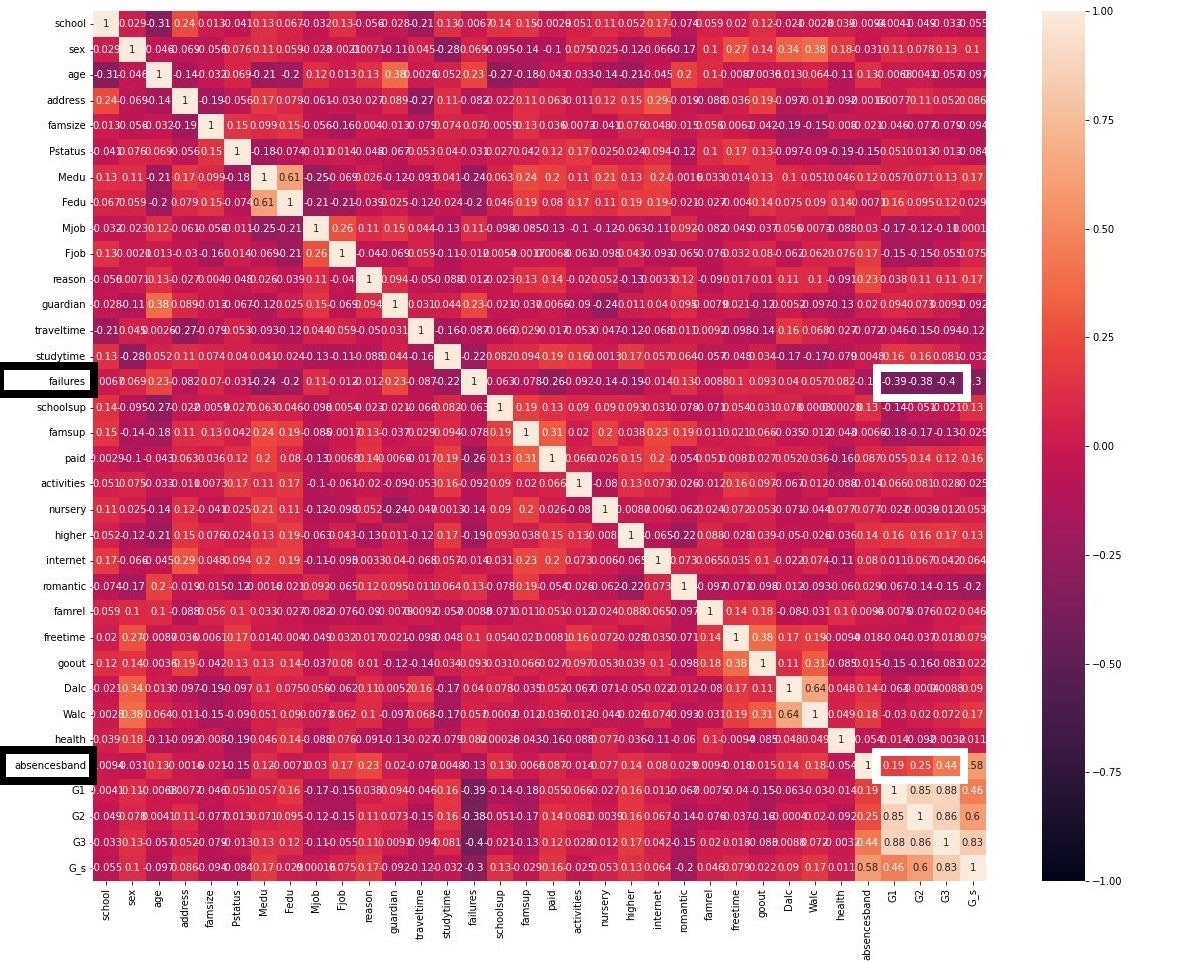
このうち、注目したのは、
__各成績(特にG3)との相関性が|0.2|を超えている特徴量__である。
詳細(図)はこちら
成績の上がった生徒は
age、address、Medu、Fedu、traveltime、failures、school sup、higher、Walc、absencesband
成績の下がった生徒は
failures、absencesband
と実際の成績に相関があった。(太字は特に相関が強い説明変数)
4.成績が上がる/下がる原因の推測
ここまでの処理で、一部の説明変数に相関があることは分かったが、実際にどのような相関があるのかを詳細に見ることで、原因の推測をしていきたい。
なお、項目の詳細は、以下の通り。
age : 生徒の年齢。
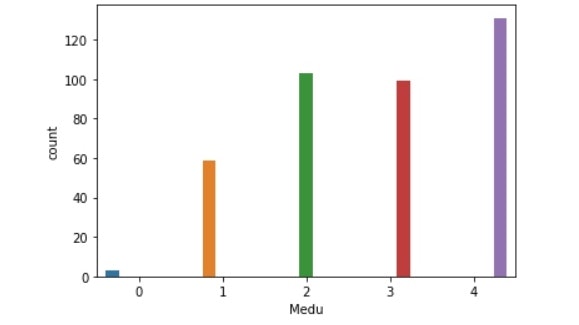
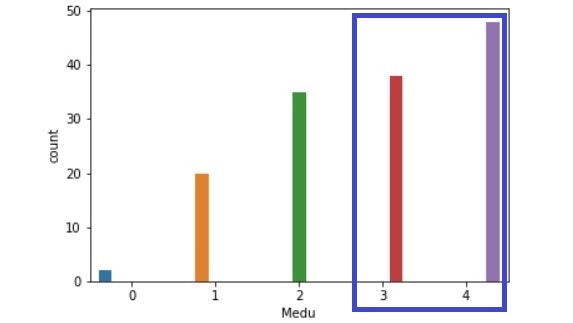
Medu : 母親の学歴。0:学歴なし、1:小卒、2:中卒、3:高卒、4:大学以降(日本の教育制度に置き換えて記載しています)
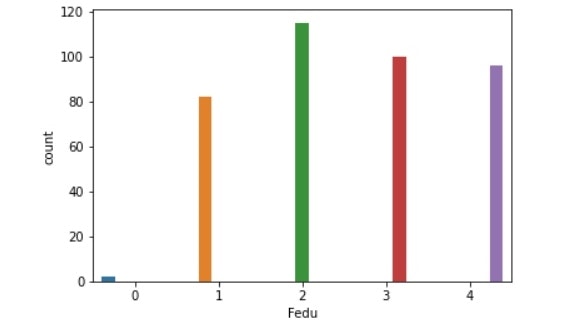
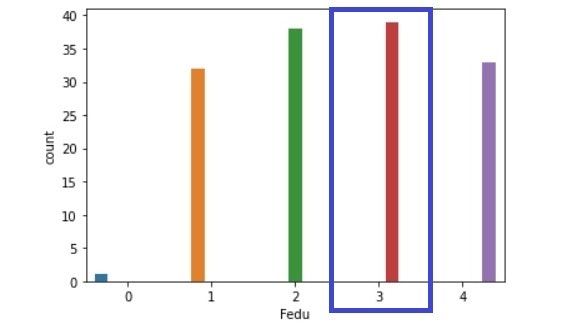
Fedu : 父親の学歴。数字はMeduと同じ。
traveltime : 通学時間。1:15分未満、2:15-30分未満、3:30分-1時間未満、4:1時間以上
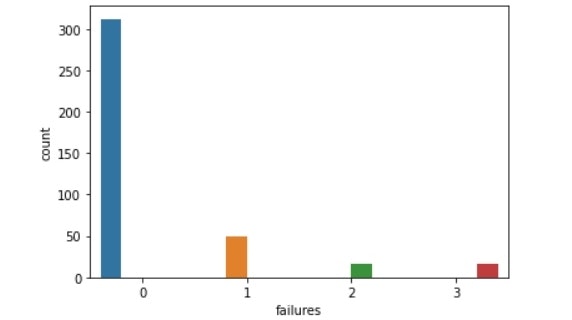
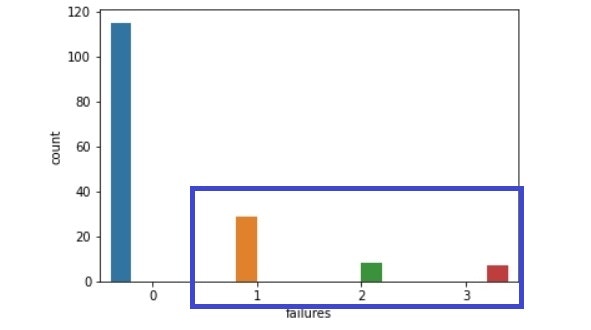
failures : 単位を落とした数。数が単位を落とした数に該当。4は4以上を表す。
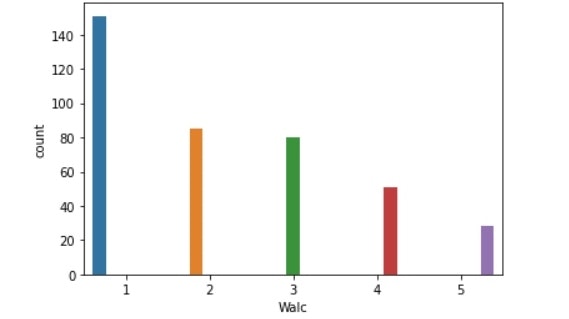
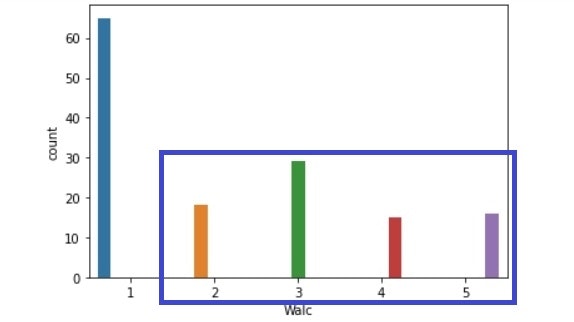
Walc : 週末のアルコール消費量。1:非常に少ない、5:非常に多い
absences(band) : 欠席数。数が欠席数に該当。
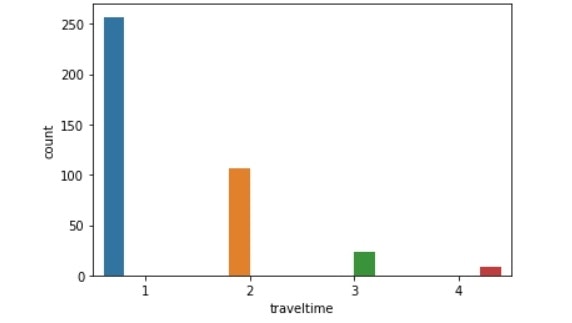
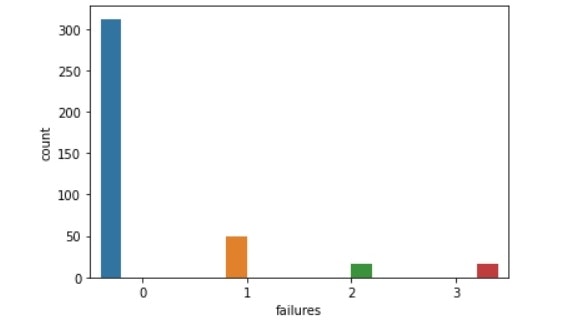
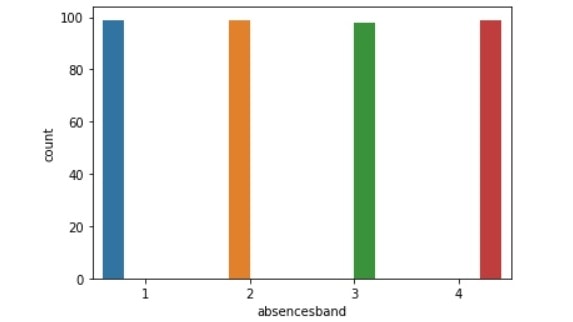
以上の各項目の分布をseabornのcountplotにてみていく。
コードはこちら
for i in data:
sns.countplot(x=i, hue=i, data=data)
plt.legend().remove()
plt.show()
for i in data_high:
sns.countplot(x=i, hue=i, data=data_high)
plt.legend().remove()
plt.show()
for i in data_low:
sns.countplot(x=i, hue=i, data=data_low)
plt.legend().remove()
plt.show()
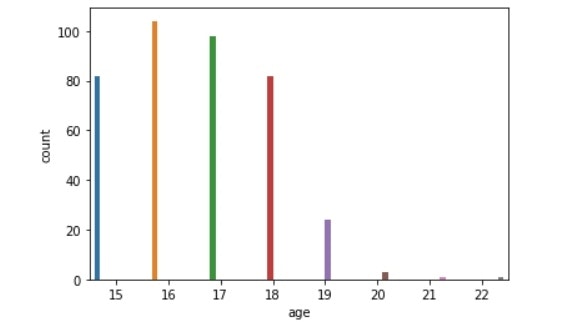
結果で示されたグラフを比較すると、各項目で多くのことが推測できた。
※特徴的な結果を示したもののみ示す。
グラフ(並べ替え済み)はこちら
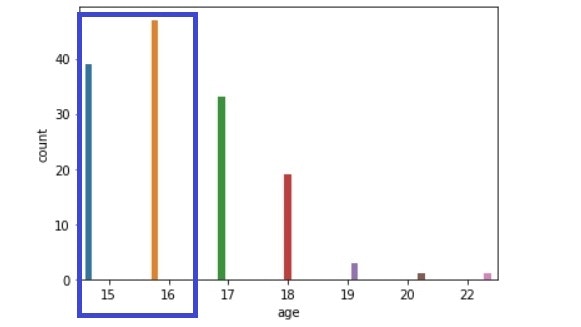
グラフから読み取れることとしては、
【成績上昇生徒】
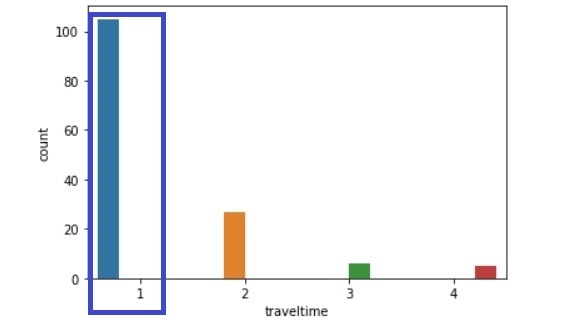
生徒全体の割合と比べて、
・年齢:15・16歳の割合が高い。
・母親の教育:3,4の割合が増えている。
・父親の教育:1,2が減り、3の割合が増えている。
・通学時間:2,3,4に比べて、1の生徒の割合が高い。
・単位を落とした数:1,2の割合が減っている。
・週末のアルコール:2以上の割合が減っている。
【成績下降生徒】
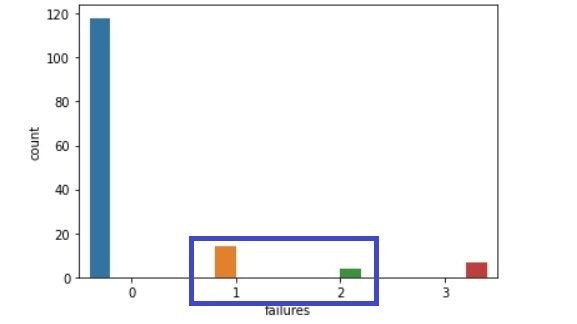
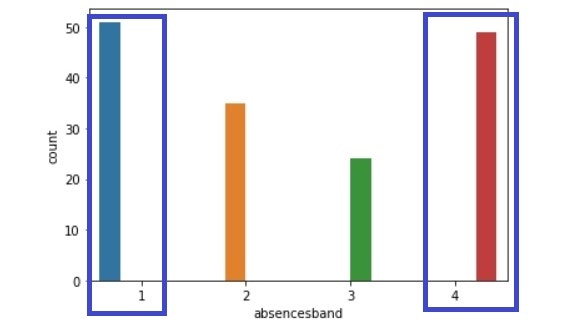
生徒全体の割合と比べて、
・単位を落とした数:1以上の割合がかなり増えている。
・欠席数:4の割合も多いが、1も多い。
よって、成績の上がる/下がる原因を以下のように推測できる。
成績が上がりやすいのは、
・年齢が若い時(1年生など、学年がまだ下の方)
・両親の学歴が高い生徒。
・学校までの通学時間が短い生徒。
・単位を落とした数が0。
・週末にアルコールをあまり飲まず、勉強など別のことに時間を使っている生徒。
一方、成績が下がりやすいのは、
・単位を落としたことがある生徒。
・欠席日数が非常に多い生徒。
・全く欠席していない生徒でも、単位を落とすほど、授業に真剣に取り組めていない生徒。
5.データを削減/統合し、モデル化
原因は推測できたため、次は目的の2つめである、精度の高いモデルの作成に取りかかった。
今回は、①成績上昇した生徒の場合と、②成績下降した生徒の場合 の2つのモデル作成を目標とする。
なお、これらの説明変数のうち、__1学期成績と、成績以外の説明変数のみを使って__学年末の成績の予測を行いたい。
ただ、成績は20段階評価となっており、それではさすがに予測が難しいため、20段階→5段階と規模を縮小して、モデルを作成する。
以下の手順で行う。
① 20段階評価を5段階評価に縮小した説明変数を追加。
② データ量の削減
③ 一部データの統合
④ 様々な手法にてモデル化
① 20段階評価を5段階評価に縮小した説明変数を追加。
20段階を5段階にしたG3rank5カラムを、以下のように設定し、目的変数に設定した。
[G3]0~4 → [G3rank5]0
[G3]5~8 → [G3rank5]1
[G3]9~12 → [G3rank5]2
[G3]13~16 → [G3rank5]3
[G3]17~20 → [G3rank5]4
コードはこちら
# rank5カラムを作成
data["G1rank5"] = data["G1"]
data["G2rank5"] = data["G2"]
data["G3rank5"] = data["G3"]
# rank5カラムに値の代入
for i in ["G1rank5", "G2rank5", "G3rank5"]:
data.loc[data[i] <= 4, i] = 0
data.loc[(5 <= data[i]) & (data[i] <= 8), i] = 1
data.loc[(9 <= data[i]) & (data[i] <= 12), i] = 2
data.loc[(13 <= data[i]) & (data[i] <= 16), i] = 3
data.loc[data[i] >= 17, i] = 4
# 各データを再設定し、目的変数を追加
data_high = data.query("G_s > 0").reset_index(drop=True)
data_mid = data.query("G_s == 0").reset_index(drop=True)
data_low = data.query("G_s < 0").reset_index(drop=True)
target_high = data_high["G3rank5"].reset_index(drop=True)
target_low = data_low["G3rank5"].reset_index(drop=True)
target = data["G3rank5"]
また、後々のモデルの精度向上度合を測るため、これ以降何も手を加えないデータのコピーを取っておく。
コードはこちら
data_ori = data.copy()
data_ori.drop(['G2', 'G3', 'G_s', 'G1rank5', 'G2rank5', 'G3rank5'], axis=1, inplace=True)
② データ量の削減
次に、これまでに確認できた、モデル作成の際の邪魔になりそうな成績と相関性の弱い説明変数を削除しておく。
なお、ここから成績上昇生徒と成績下降生徒で分けて考えていく。
コードはこちら
# 相関性の薄いカラムの指定
drop_col_high = ['school', 'sex', 'famsize', 'Pstatus',
'Mjob', 'Fjob', 'reason', 'guardian', 'studytime',
'famsup', 'paid', 'activities', 'nursery',
'internet', 'romantic', 'famrel', 'freetime', 'goout', 'Dalc', 'health', 'G2']
drop_col_low = ['school', 'sex', 'age', 'address', 'famsize', 'Pstatus', 'Medu', 'Fedu',
'Mjob', 'Fjob', 'reason', 'guardian', 'traveltime', 'studytime',
'schoolsup', 'famsup', 'paid', 'activities', 'nursery',
'higher', 'internet', 'romantic', 'famrel', 'freetime', 'goout', 'Dalc',
'Walc', 'health', 'G2']
drop_col_all = ['school', 'sex','famsize', 'Pstatus',
'Mjob', 'Fjob', 'reason', 'guardian', 'studytime',
'famsup', 'paid', 'activities', 'nursery',
'internet', 'romantic', 'famrel', 'freetime', 'goout', 'Dalc',
'health', 'G2']
# 指定したデータの削除
data_high.drop(drop_col_high, axis=1, inplace=True)
data_low.drop(drop_col_low, axis=1, inplace=True)
data.drop(drop_col_all, axis=1, inplace=True)
③ 一部データの統合
次に、「4.成績が上がる/下がる原因の推測」のseabornのcountplotの結果から、統合できるデータを統合し、モデルの精度向上を試みた。
【成績上昇生徒】
まずは成績上昇生徒の説明変数を統合した。
age : 17歳以下と18歳以上で分けた。(16歳以下で分けてもよかったが、18歳以上のグラフが特に大きく変動していたため、こちらで分けた)
travelband : 1と、それ以外で分けた
Walcband : 1と、それ以外で分けた
failuresband : 0と、それ以外で分けた
コードはこちら
# 各追加予定のカラムを作成した
data_high["ageband"] = data_high["age"]
data_high["travelband"] = data_high["traveltime"]
data_high["Walcband"] = data_high["Walc"]
data_high["failuresband"] = data_high["failures"]
# 条件ごとにカラムを統合した
data_high.loc[data_high["ageband"] <= 17, "ageband"] = 0
data_high.loc[data_high["ageband"] >= 18, "ageband"] = 1
data_high.loc[data_high["failuresband"] == 0, "failuresband"] = 0
data_high.loc[data_high["failuresband"] != 0, "failuresband"] = 1
for i in ["travelband", "Walcband"]:
data_high.loc[data_high[i] <= 1, i] = 0
data_high.loc[data_high[i] >= 2, i] = 1
# 不要なデータを削除
drop_col = ['age', 'traveltime', 'Walc', "failures", "G3",
'G_s', 'G1rank5', 'G2rank5', 'G3rank5']
data_high.drop(drop_col, axis=1, inplace=True)
コードはこちら
# failuresのカラムを作成し、統合した
data_low["failuresband"] = data_low["failures"]
data_low.loc[data_low["failuresband"] == 0, "failuresband"] = 0
data_low.loc[data_low["failuresband"] != 0, "failuresband"] = 1
# 不要なデータを削除
data_low.drop(["failures", "G3", 'G_s', 'G1rank5', 'G2rank5', 'G3rank5'], axis=1, inplace=True)
④ 様々な手法にてモデル化
データの削減、統合を終え、いよいよ最後のモデルの精度測定に取りかかる。
今回はKFoldにて、学習用データと検証用データに分け、モデル化を行う。
まずは、手法の説明をする。
以下の手法をすべて試し、最も精度の高いモデルをbest modelとする。
・LogisticRegression(solver='liblinear') - ロジスティック回帰
線形分離可能なデータの境界線を学習によって見つけて、データの分類を行う手法。
二項分類などクラスの少ないデータに使われる。
・LinearSVC - 線形サポートベクターマシン
ロジスティック回帰と同じく、データの境界線を見つけ、データの分類を行う手法。
分類する境界線が2クラス間の最も離れた場所に引かれて、二項分類を行う。
・SVC - 非線形サポートベクターマシン
カーネル関数と呼ばれる変換式に従って、数学的処理を行いデータを線形分離可能に変換する。
二項分類などクラスの少ないデータに使われる。
・DecisionTreeClassifier - 決定木
説明変数一つ一つに着目し、その変数内のある値を境にデータを分割し、データの属するクラスを決定する手法。
線形分離可能なデータに使われる。
・RandomForestClassifier - ランダムフォレスト
決定木の簡易版のモデルを複数作り、分類の結果をモデルの多数決で決める手法。
線形分離可能でないデータにも使用可能。
・Perceptron - パーセプトロン
複数の入力データに対し、一つの値を出力する、人間の脳神経回路を真似た手法。
ディープラーニングの大本となるアルゴリズムを持つ。
【元データ】
まずは元データ(ほぼチューニングなしのデータ)でモデルを作成する
※成績データ(1学期除く)以外の全てのデータを使用している
コードはこちら
from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score
# KFoldにてデータを5分割
cv = KFold(n_splits=5, shuffle=False, random_state=0)
# 様々なモデルを使い、各精度を測定
for j in [LogisticRegression(solver="liblinear"), SVC(), LinearSVC(), RandomForestClassifier(),
DecisionTreeClassifier(), Perceptron()]:
AccBox = []
for i, (train_index, val_index) in enumerate(cv.split(data_ori)):
X_train, X_val = data_ori.loc[train_index], data_ori.loc[val_index]
y_train, y_val = target.loc[train_index], target.loc[val_index]
model = j
model.fit(X_train, y_train)
acc = model.score(X_val, y_val)
print(i, acc)
AccBox.append(acc)
print(j, ":", np.mean(AccBox))
精度は、以下の通り。
LogisticRegression(solver='liblinear') : 0.579746835443038
SVC() : 0.6075949367088608
LinearSVC() : 0.5468354430379747
RandomForestClassifier() : 0.6354430379746836
DecisionTreeClassifier() : 0.5746835443037974
Perceptron() : 0.47341772151898737
best model : RandomForestClassifier
best score : 0.6354430379746836
【成績上昇生徒】
次に成績上昇生徒のデータでモデルを作成する
※使用した説明変数は、['Medu', 'Fedu', 'G1', 'address', 'schoolsup', 'higher', 'absencesband',
'ageband', 'travelband', 'Walcband', 'failuresband']
コードはこちら
from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score
# KFoldにてデータを5分割
cv = KFold(n_splits=5, shuffle=False, random_state=0)
# 様々なモデルを使い、各精度を測定
for j in [LogisticRegression(solver="liblinear"), SVC(), LinearSVC(), RandomForestClassifier(),
DecisionTreeClassifier(), Perceptron()]:
AccBox2 = []
for i, (train_index, val_index) in enumerate(cv.split(data_high)):
X_train, X_val = data_high.loc[train_index], data_high.loc[val_index]
y_train, y_val = target_high.loc[train_index], target_high.loc[val_index]
model = j
model.fit(X_train, y_train)
acc = model.score(X_val, y_val)
print(i, acc)
AccBox2.append(acc)
print(j, ":", np.mean(AccBox2))
best model : SVC
best score : 0.8320197044334975
【成績下降生徒】
次に成績下降生徒のデータでモデルを作成する
※使用した説明変数は、['G1', 'absencesband', 'failuresband']
コードはこちら
from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score
# KFoldにてデータを5分割
cv = KFold(n_splits=5, shuffle=False, random_state=0)
# 様々なモデルを使い、各精度を測定
for j in [LogisticRegression(solver="liblinear"), SVC(), LinearSVC(), RandomForestClassifier(),
DecisionTreeClassifier(), Perceptron()]:
AccBox3 = []
for i, (train_index, val_index) in enumerate(cv.split(data_low)):
X_train, X_val = data_low.loc[train_index], data_low.loc[val_index]
y_train, y_val = target_low.loc[train_index], target_low.loc[val_index]
model = j
model.fit(X_train, y_train)
acc = model.score(X_val, y_val)
print(i, acc)
AccBox3.append(acc)
print(j, ":", np.mean(AccBox3))
print(data_low.columns)
best model : SVC
best score : 0.8241935483870968
まとめると、
各ベストスコアは、
元データ:0.6354430379746836 (RandomForestClassifier)
成績上昇生徒:0.8320197044334975 (SVC)
成績下降生徒:0.8241935483870968 (SVC)
元データに比べて、結果も0.2程度向上しており、単体で見ても0.8を超える精度を誇るので、成績上昇生徒・成績下降生徒ともに質の高いモデルが作れたのではないかと思う。
6.校舎の生徒の成績向上を促進/阻害する要因の推測
これまでの分析で、「4.成績が上がる/下がる原因の推測」で行った推測の信憑性は高まっている。
この分析をもとに、自分の校舎の生徒の成績に影響しており、修正可能なものを推測したい。
4で行った成績が上がる/下がる原因の推測内容
成績が上がりやすいのは、 ・年齢が若い時(1年生など、学年がまだ下の方) ・両親の学歴が高い生徒。 ・学校までの通学時間が短い生徒。 ・単位を落とした数が0。 ・週末にアルコールをあまり飲まず、勉強など別のことに時間を使っている生徒。 一方、成績が下がりやすいのは、 ・単位を落としたことがある生徒。 ・欠席日数が非常に多い生徒。 ・全く欠席していない生徒でも、単位を落とすほど、授業に真剣に取り組めていない生徒。それ以外の項目に対して、予測を立てた。
・年齢が若い時(1年生など、学年がまだ下の方)
→__受験生でない、1年生や2年生のうちに学習習慣を身に着けておく__と、今後良い成績を取ることができる。
・学校までの通学時間が短い生徒。
→通学時間・距離が長いことで、__疲れること、余裕がないこと__が予想できる。
疲れた状態で勉強しても、集中力は続かない。だらだらとした勉強時間だけが長くなりがち、それなら、早起きして早く学校に行き、__余裕をもって勉強すること__や、家にまっすぐ帰り__しっかり休憩した後に勉強量(自分の時間)を確保すること__が成績向上につながるようだ。(起きる時間や寝る時間のデータは今回のデータセットには存在しなかった。また、勉強時間は成績向上にあまり影響しないという結果は出ている。)
・単位を落とした数が0。
→__1年生からコツコツやること__が大切。3年生から頑張る人ほど、成績は上がらない。
これに成績下降の要因も加えると、以下のように推測できるのではないかと考えた。
・まず、__疲れている状態で勉強をしないこと__が大切。通学で疲れながら勉強するのではなく、__適度な休憩を取って、短期集中で効率よく勉強する__方が成績向上につながりやすい。
・1年生からコツコツ勉強することが重要。また、卒業まで学校の授業はしっかり出席するだけではダメで、授業中に集中力を切らさないこと。テストを落としすぎないこと。
・自由時間や、恋愛、インターネットの使用量などは関係ない。趣味を楽しみながらも、自分がどれだけ効率よく、集中して勉強できるかだけが重要。
7.反省点と今後の展望
今回、成績の上がる/下がる原因の推測もでき、モデルの作成もできたことに対しては良かったと思う。ただ、反省点はまだまだ多い。
・データ数が少なく、学習用データとテスト用データを分けられなかったこと
・日本のデータでない
・他のデータセットと合わせられなかった
・どうしても三学期成績が一学期成績に依存しすぎてしまうこと(本当は一学期成績も使わずに成績予測を行いたかった) etc…
今後は、別のデータ数の多いデータセットを見つけ、それと相関をとりながら、今回の予測が誤りでなかったことを実証したい。また、教科ごとに原因を探れるような分析をしていきたい。
ただ、今回の結果はそれなりに良い予測ができたとは思う。生徒との実際の面談で使おうと思う。
長々とお付き合いありがとうございました。
少しでも皆様の教育の手助けとなれば幸いです。