Semigroup型クラス 〜型クラスで見るPureScript〜

※この記事は「型クラスで見るPureSciript」の連載記事です。
（前回投稿からかなり時間が立ってしまいました。ストックしていたものから順に投稿再開していきます。）

くっつけて、くっつけて、さらに、くっつけて

今回はSemiGroup型クラスについて見ていきます。Semigroupとは日本語で__半群__（はんぐん）と呼ばれる代数構造です。と言っても、あぁ__半群__のことかと納得する人は少ないでしょう。そこで、まずはプログラマなら誰でも知っている例を見てみましょう。

Semigroup型クラスの一番身近な例は__文字列__です。SemiGroup型クラスというのは__結合演算__が定義された型クラスです。これまで何度も出てきている結合演算子<>は、実はSemigroup型クラスで定義されている演算子だったのです。例を見てみましょう。

> "abc" <> "de"
"abcde"

> "abc" <> "de" <> "f"
"abcdef"

ここで注目すべきは、__文字列と文字列を結合した結果も文字列になる__という点です。なんだ、あたりまえじゃないかと思う方もいることでしょう。でも、これがSemigroup型クラスの重要な性質なのです。

半群ってなぁに？

それでは__半群__の定義について見てみましょう。数学的な__半群__の定義は次のようになります。

1. 集合 $G$ の元 $a,b\in G$ に対して、$$c=a<>b,\;\;c\in{}G$$となるような結合演算$<>$が定義されている
2. 結合律：$$(a<>b)<>c==a<>(b<>c)$$ が成り立つ。

なんかよくわからん……って方が多いのではないでしょうか。先ほどの文字列の例に当てはめながら、１つずつ見てみましょう。

まず１つ目は、__結合演算__をしても元のデータ型のままであるということです。先ほど言った、__文字列と文字列を結合した結果も文字列になる__というのは、この条件を満たしています。

２つ目の結合律については、足し算や掛け算の場合は中学校で習ったことがあるでしょう。結合演算が連続するときに、どの順番で結合演算を実行しても同じ結果になるということです。

結合律が成り立つことで"abc"<>"de"<>"f"のように括弧を使わずに続けて書いても、計算結果が曖昧にならずに済みます。（実際の処理は右結合で評価されています。）

数学では__結合演算__という言い方をすることは少なく、結合演算<>は掛け算*と同一視されることが多いです。また、可換群の場合は足し算+と同一視されることもあります。PureScriptでは、あえて__結合演算__を別の演算子として定義しています。

Semigroup型クラス

それでは、Semigroup型クラスについて学んでみましょう。Semigroup型クラスは、次のように定義されています。

class Semigroup a where
  append :: a -> a -> a

このappend関数が__結合演算__を定義する関数です。__結合演算__の存在は定義されていますが、__結合律__に関する制約は定義上何も書かれていません。これは、プログラマがSemigroup型クラスを実装する際に守るべき__制約__として扱われています。

ちなみに、日本語にすると、どちらも「結合」という言葉が出てきて紛らわしいですが、結合律は英語で"associativity"であり、"append"とは全然違う単語です。混同しないように注意しましょう。

Semigroup型クラスの例１　２次元回転群

ところで、Semigroup型クラスって__文字列結合__以外に使い道あるの？って思う方も多いでしょう。Stringデータ型以外には、Arrayデータ型なんかにもSemigroup型クラスが実装されていますが、あまり、単純すぎる例を見ても分かった気がしないので、少し違う例を見て見ましょう。

data Rotation = Rotation Int

instance showRotation :: Show Rotation where
  show (Rotation n) = "Rotation " <> show (mod n 360)

instance eqRotation :: Eq Rotation where
  eq (Rotation n) (Rotation m) = 0 == mod (n - m) 360

Rotationデータ型は、１°を最小単位とする２次元回転を表すデータ型です。上のコードを見ると、前に作った角度を表すデータ型Degreeと類似していることが分かります。異なる点は、append関数を利用して、２つの回転を合成できる点です。

append関数を定義するSemigroup型クラスの実装は次のようになります。

instance semigroupRotation :: Semigroup Rotation where
  append  (Rotation n) (Rotation m)
    = Rotation $ mod (n + m) 360

２つの回転を合成するには、単に回転角を足し合わせれば良いのですが、360°の違いを同一視するために剰余を計算しています。これをPCSIで試すと次のようになります。

> (Rotation 20) <> (Rotation 30)
Rotation 50

> (Rotation 120) <> (Rotation 300)
Rotation 60

> (Rotation (-20)) <> (Rotation (-40))
Rotation 300

このように、２つの回転を合成することができました。

Semigroup型クラスの演算子

Semigroup型クラスで定義されている演算子は、これまでなんども出てきている結合演算子<>だけです。

infixr 5 append as <>

これまで、文字列の場合に何度も使用して慣れ親しんでいる演算子なので、特にコメントすることもないでしょう。あえて一言加えるなら、<>は他の言語では"not equals"の意味で使われることが多い記号なので、初心者が混乱しないように注意することくらいでしょうか。

Semigroup型クラスの例２　五角形の対称群

先ほどの２次元回転群では、あまり理解が深まらないと思いますので、もう少し込み入った例を見てみましょう。

data PentaSymmetry = PentaRot Int | PentaRef Int

instance showPentaSymmetry :: Show PentaSymmetry where
  show (PentaRot n) = "PentaRot " <> show n
  show (PentaRef n) = "PentaRef " <> show n

instance eqPentaSymmetry :: Eq PentaSymmetry where
  eq (PentaRot n) (PentaRot m) = 0 == mod (n - m) 5
  eq (PentaRef n) (PentaRef m) = 0 == mod (n - m) 5
  eq _ _ = false

PentaSymetryデータ型は、五角形の対称群を表すデータ型です。PentaSymetryデータ型は、２つの型構築子を持ち、PentaRot構築子は72°ずつの回転変換を表す値を構築します。それに対し、PentaRef構築子は五角形の各頂点と中心点を通るような線を軸とした反転変換を表す値を構築します。

多角形の対称群は群論の教科書に最初に出てくる簡単な例なのですが、「なんのことかさっぱり」という方が多いと思いますので絵を描いて解説しましょう。

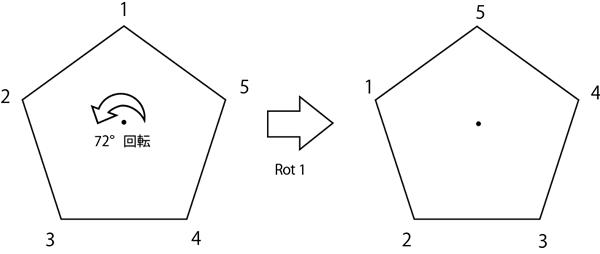
まずは、回転変換についてです。PentaRot 1は反時計回りに72°回転する変換を表します。図にすると下図のようになります。同様に、PentaRot nは反時計回りにn×72°回転する変換を表します。

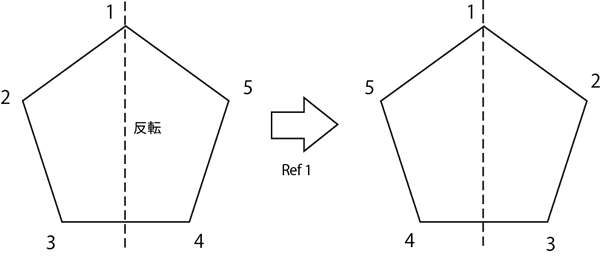
つぎに、反転変換についてです。PentaRef 1は頂点1を通るような軸に対して反転させる変換を表します。図にすると下図のようになります。同様に、PentaRef nは頂点nを通るような軸に対する反転変換を表します。

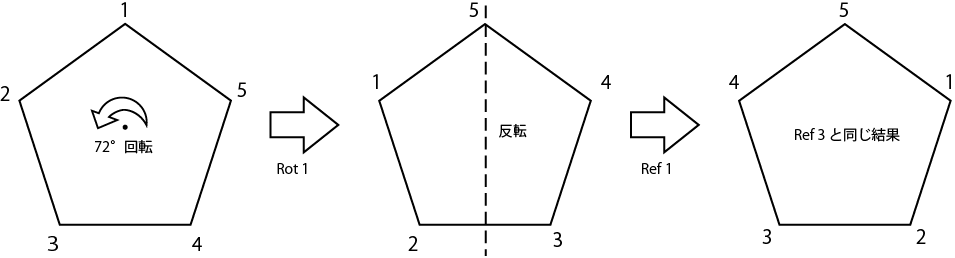
複数の変換を続けて行うことを__変換の合成__と言います。PentaRot 1とPentaRef 1の合成を図形を使って考えてみましょう。

すると、PentaRot 1とPentaRef 1の合成はPentaRef 3と同じ結果になります。このように、PentaSymetryデータ型の値同士を合成するとPentaSymetryデータ型の別の値になることが分かります。この性質を整理してSemigroup型クラスを実装すると次のようになります。

instance semigroupPentaSymmetry :: Semigroup PentaSymmetry where
  append (PentaRot n) (PentaRot m) = PentaRot $ mod (n + m) 5
  append (PentaRef n) (PentaRot m) = PentaRef $ mod (n + 2 * m) 5
  append (PentaRot n) (PentaRef m) = PentaRef $ mod (3 * n + m) 5
  append (PentaRef n) (PentaRef m) = PentaRot $ mod (2 * n + 3 * m) 5

それでは実際に試してみましょう。これは数学の慣例なのですが、__変換は右から先に適用する__作法なので、PentaRot 1とPentaRef 1の合成はPentaRef 1 <> PentaRot 1と書きます。

> PentaRef 1 <> PentaRot 1
PentaRef 3

どうでしょうか。納得できない場合は、色々なパターンの絵を描いて、演算結果と比較して見てください。

Semigroup型クラスの例３　数値の桁を表すデータ型

最後に、少し変な例を作って試してみましょう。

data Digit = Digit Int

instance showDigit :: Show Digit where
  show (Digit n) = "Digit " <> show (abs n)

instance eqDigit :: Eq Digit where
  eq (Digit n) (Digit m) = (abs n) == (abs m)

Digitデータ型は数字の桁を表すデータ型です。と説明しても、うまく意味が伝わらないと思います。上の定義だけでは、単に自然数を表しているだけなので、先にSemigroup型クラスを実装してから解説しましょう。

instance semigroupDigit :: Semigroup Digit where
  append (Digit n) (Digit m) = Digit (n' * pow 10 (len m' 1) + m')
    where
      n' = abs n
      m' = abs m
      len m acc
        | m < pow 10 acc = acc
        | otherwise      = len m (acc+1)

サブ関数が定義されていたりして、これまでと比べると、なんだか複雑な実装です。この挙動を理解するには試してみた方が早いでしょう。

> Digit 1 <> Digit 23
Digit 123

> Digit 12 <> Digit 3
Digit 123

試してみるとわかる通り、Digitデータ型は数字に対して文字列結合のような演算を行うことができます。__結合律__も試してみましょう。

> (Digit 1 <> Digit 23) <> Digit 456
Digit 123456

> Digit 1 <> (Digit 23 <> Digit 456)
Digit 123456

このように、数値の桁同士を結合する演算も__半群__になっていることが分かります。

くっつきむしは怖くない

今回は__半群__という聞きなれない言葉が出てきました。__半群__という言葉は、大学の理系学部でも数学を多用する一部の専門分野以外では習わない言葉だと思います。しかし、実際に試してみると、世の中にある当たり前の概念を小難しい言葉を使って言い直しただけだと分かります。

PureScriptなどの関数型言語では、こうした数学用語が沢山でてくるようですが、聞きなれない言葉に惑わされずに、感覚で理解できれば、それほど難しくなかったりします。こういった数学的概念を理解するには、当たり前の例と、当たり前ではない例の両方を見てみると、なんとなく分かった気がしてくるものです。

次回は、Monoid型クラスを解説する予定です。

演習問題

1. （簡単）
   
   倍率を表すデータ型Ratioを定義し、Semigroup型クラスを利用して、倍率の合成演算を定義してください。
2. （難しい）
   
   正方形の対称群を表すデータ型SquareSymmetryを定義し、Semigroup型クラスを実装してみてください。
   （ヒント：正方形の場合、向かい合う頂点を結ぶ対称軸と、向かい合う辺の中点を結ぶ対称軸の２種類（計４本）の反転軸が存在します。）

参考文献

Semigroup型クラスについては下記を参考にしました。

• https://pursuit.purescript.org/packages/purescript-prelude/4.0.0/docs/Data.Semigroup
• https://github.com/purescript/purescript-prelude/blob/v4.0.0/src/Data/Semigroup.purs

また、半群については下記を参考にしました。

• https://ja.wikipedia.org/wiki/%E5%8D%8A%E7%BE%A4