※この記事は「型クラスで見るPureSciript」の連載記事です。
※絵文字フォントがインストールされていない環境では一部の文字が表示されない場合があります。
大きいか小さいか
前回はデータの値が等しいか等しくないかを判定するEq型クラスについて学び、(==)演算子と(/=)演算子を導入しました。等しいか等しくないかを判定できるようになると、次は__大きいか小さいか__を判定できるようにしたいというのは自然な流れです。
今回はデータの値を比較して__大きいか小さいか__を判定するOrd型クラスについて学んで見ましょう。その前に、__大きいか小さいか__とはどういう概念なのかもう一度おさらいしてみましょう。
私たちは小学校で、ものの数が__多いか少ないか__という概念を習いました。例えば、2個のリンゴと3個のリンゴを比較して、2個のリンゴの方が__少ない__、または、3個のリンゴの方が__多い__と表現します。これを記号で表すと、こんな感じになります。
$$🍎🍎\lt🍎🍎🍎$$
あるいは、大きさの違う2つのリンゴを比較して、左のリンゴの方が__小さい__とか、右のリンゴの方が__大きい__とか表現します。これも記号で表すと、こんな感じです。
$$🍎\lt\Huge🍎$$
簡単ですね。では、この__大きいか小さいか__という概念をロジックとして組み立てるにはどうしたらよいか見ていきましょう。
順序集合ってなんだろう
__大きいか小さいか__という概念をロジックとしてプログラムに組み込むには、数学の__順序集合__の考え方を利用することで実現することができます。__順序集合__とは集合内の2つの要素に対して大小関係を定義した集合のことをいいます。
__順序集合__では、$a$ が $b$ 以下であることを $a<=b$と表します。反対に、$b$ が $a$ 以上であることを $b>=a$ と表します。数学では、この関係演算子 $<=$ は、次の条件を満たす必要があるとされています。
- 反射律 : $a <= a$
「$a$ は $a$ 自身と等しいか小さい」
- 反対称律: $a <= b \;\text{and}\; b <= a \;\Rightarrow\; a == b$
「$a$ が $b$ 以下で、$b$ が $a$ 以下であれば、$a$ と $b$ は等しい」
- 推移律 : $a <= b \;\text{and}\; b <= c \;\Rightarrow\; a <= c$
「$a$ が $b$ 以下で、$b$ が $c$ 以下であれば、$a$ は $c$ 以下」
いちいち $<$ と $=$ がくっついているのが若干煩わしいですが、私たちの日常の感覚に反していないことは、少し考えると分かるでしょう。
このままでも十分有用なのですが、数学的な定義よりも、プログラマの都合を優先して、後で少し書き換えてみます。細かい定義は脇に置いて、実際に使いながら理解していきましょう。
Ord型クラス
それでは、Ord型クラスについて見てみましょう。Ord型クラスは次のように定義されています。
class Eq a <= Ord a where
compare :: a -> a -> Ordering
ここで、Orderingデータ型というのは、列挙型のようなもので、次のように定義されています。
data Ordering = LT | GT | EQ
LTは"less than"、GTは"greater than"、EQは"equal"の略です。compare a bは、$a \lt b$ の時にLTを、$a==b$ の時にEQを、$a \gt b$ の時にGTを返却する関数として定義します。
Ord型クラスの例1 長さを表すデータ型
それでは、早速、Ord型クラスを実装してみましょう。前回作成したLengthデータ型についてOrd型クラスを実装すると、次のようになります。
instance ordLength :: Ord Length where
compare (Inch k) (Inch l) = compare k l
compare (CentiMetre k) (CentiMetre l) = compare k l
compare (Inch k) (CentiMetre l) = compare (k * 2.54) l
compare (CentiMetre k) (Inch l) = compare k (l * 2.54)
特に、難しい箇所はないと思います。あえて、解説するならNumber型のcompare関数を利用している点でしょうか。型クラスのメンバ関数は型推論によって適切なインスタンスの関数が呼び出されます。それでは、試してみましょう。
> compare (CentiMetre 1.0) (CentiMetre 2.54)
LT
> compare (CentiMetre 2.54) (Inch 1.0)
EQ
> compare (Inch 1.0) (CentiMetre 1.0)
GT
Ord型クラスの演算子
それではOrd型クラスの演算子について見ていきましょう。前回は、演算子を定義する関数から見ていきましたが、今回からは演算子表現が定義されている関数は演算子と一緒に見ていきましょう。
(<)演算子
(<)演算子は他の言語でもお馴染みの大小関係を表す不等号演算子です。PureScriptでは次のように宣言されています。
lessThan :: forall a. Ord a => a -> a -> Boolean
infixl 4 lessThan as <
この演算子はcompareの結果がLTの時にtureを返却します。先ほどのLengthデータ型を使って試してみましょう。
> (CentiMetre 1.0) < (CentiMetre 2.54)
true
> (CentiMetre 2.54) < (Inch 1.0)
false
> (Inch 1.0) < (CentiMetre 1.0)
false
(<=)演算子
次は(<=)演算子です。数学記号の「$\leq$」に相当します。(イコールと他の記号を組み合わせた時に、イコールが1本線になるのが欧米式です。)これは次のように宣言されています。
lessThanOrEq :: forall a. Ord a => a -> a -> Boolean
infixl 4 lessThanOrEq as <=
お分かりだと思いますが、(<=)演算子はcompareの結果がLTまたはEQの時にtureを返却します。これも試してみましょう。
> (CentiMetre 1.0) <= (CentiMetre 2.54)
true
> (CentiMetre 2.54) <= (Inch 1.0)
true
> (Inch 1.0) <= (CentiMetre 1.0)
false
(>)演算子
今度は(>)演算子です。宣言は次のようになっています。
greaterThan :: forall a. Ord a => a -> a -> Boolean
infixl 4 greaterThan as >
(>)演算子は(<)演算子の逆の演算子ですね。compareの結果がGTの時にtureを返却します。どんどん試しましょう。
> (CentiMetre 1.0) > (CentiMetre 2.54)
false
> (CentiMetre 2.54) > (Inch 1.0)
false
> (Inch 1.0) > (CentiMetre 1.0)
true
(>=)演算子
最後は(>=)演算子です。数学記号の「$\geq$」に相当します。
greaterThanOrEq :: forall a. Ord a => a -> a -> Boolean
infixl 4 greaterThanOrEq as >=
もう、何も言うことはありませんね。試すが一番です。
> (CentiMetre 1.0) >= (CentiMetre 2.54)
false
> (CentiMetre 2.54) >= (Inch 1.0)
true
> (Inch 1.0) >= (CentiMetre 1.0)
true
Ord型クラスの例2 角度を表すデータ型
さて、同じデータ型ばかり試していても理解が深まらないので、前回作成したもう1つの例 Degreeデータ型に対しても、Ord型クラスを実装してみましょう。
ところで、角度の大小比較はどのように行えばよいでしょうか? 例えば、30°と31°を比較するなら31°の方が大きい気がします。では、30°と389°だったらどうでしょう? 数値的には389°の方が大きいように見えますが、389°は29°と等しいので30°の方が大きいと判断するのが正しそうです。
角度には反対周りというものもあります。反時計回りを正の数で表すと、時計回りは負の数で表現されます。30°と-30°ではどちらが大きいでしょうか? 0°からの差異という観点で比較すると、30°と-30°は同順と判定したいところです。
上のような事情を考慮すると、Degreeデータ型に対するOrd型クラスの実装は次のようになります。
instance ordDegree :: Ord Degree where
compare (Degree n) (Degree m)
= compare (normalize n) (normalize m)
where
normalize l
| l < 0 = normalize (-l)
| l > 180 = normalize (l - 360)
| otherwise = l
若干、定義が複雑になってきました。補助関数normalizeは角度の値を0°から180°の範囲内に収める関数です。先ほど考慮した性質を満たしているか試してみましょう。
> compare (Degree 30) (Degree 31)
LT
> compare (Degree 30) (Degree 389)
GT
> compare (Degree 30) (Degree (-30))
EQ
目論見どおりの結果となりました。
Ord型クラスの関数
それでは、Ord型クラスに対して定義されている便利な関数を幾つか見ていきましょう。
min 関数
min :: forall a. Ord a => a -> a -> a
min関数は2つの値を比較して小さい方を返却する関数です。実行結果は次のようになります。
> min (Degree 30) (Degree 31)
Degree 30
> min (Degree 30) (Degree 389)
Degree 389
> min (Degree 30) (Degree (-30))
Degree 30
max 関数
max :: forall a. Ord a => a -> a -> a
max関数はmin関数の逆ですね。2つの値を比較して大きい方を返却します。実行してみましょう。
> max (Degree 30) (Degree 31)
Degree 31
> max (Degree 30) (Degree 389)
Degree 30
> max (Degree 30) (Degree (-30))
Degree 30
clamp 関数
clamp :: forall a. Ord a => a -> a -> a -> a
clamp関数は値の範囲を指定して、範囲からはみ出した値を範囲内に収める関数です。例えば、関数h1を次のように定義してみます。
h1 :: Degree -> Degree
h1 = clamp (Degree 30) (Degree 45)
h1は、引数の値が30°〜45°の範囲内であれば、引数の値をそのまま返します。もし、引数の値が下限値30°より小さければ、下限値まで押し上げて30°を返却します。逆に、上限値45°より大きければ、上限値まで押し下げて45°を返却します。
> h1 (Degree (-35))
Degree -35
> h1 (Degree 29)
Degree 30
> h1 (Degree (-314))
Degree 45
若干、分かりにくいですかね? 紙に図を描きながら検証してみてください。
between 関数
between :: forall a. Ord a => a -> a -> a -> Boolean
between関数はclamp関数と似ていますが、こちらは範囲内に収まっているかどうかをBoolean型で返却します。先ほどと同じように関数h2を定義して試してみましょう。
h2 :: Degree -> Boolean
h2 = between (Degree 30) (Degree 45)
実行結果は次のようになります。
> h2 (Degree (-35))
true
> h2 (Degree 29)
false
> h2 (Degree (-314))
false
毎回、すべての引数を指定してもよいのですが、clamp関数やbetween関数を使う際は、上記のh1やh2のようなカリー化された関数を定義して再利用することが多いのではないでしょうか。
等しくないけど同じやつ??
ところで、見識のある皆さんはお分かりになられたでしょうか? これまでの話の中に、幽...ではなくて、おかしな所があったことを?
それは、Degreeデータ型において、eq a b == trueとなる条件とcompare a b == EQとなる条件が異なるように実装されている点です。
これは、数学的には由々しき事態です。なぜなら、順序集合の定義で紹介した反対称律を満たさなくなってしまうからです。Degree 30 <= Degree (-30)とDegree (-30) <= Degree 30の結果は、どちらもtrueでありながら、値としてはDegree 30 /= Degree (-30)であるのです。
しかし一方で、これはプログラミングの立場からするとよくあることです。実際の業務ロジックを組んでいると、上位のキーに関してはソート順として重要であっても、下位のキーに関するソート順は気にしないような事はよくあることです。この場合、下位のキーに関する順序は不定となります。ソートロジック実装によっては、入力順とは異なる順序になることもあります。
ここで学んでおくべきことは、__値としては異なる__が__順序としては順不同で同等__であるような実装ができてしまうということです。このような実装は、あまり推奨されるものではない一方で、現実問題としては、やはり有り得るのです。
これは他の言語でも時々話題に挙がる話で、例えば、Java言語のComparableインターフェースのドキュメントでもequalsとcompareToが一貫性を持たない場合は、そのことを明記するように強く推奨されていますし、一部のライブラリの動作は保証されなくなると書いて有ります。
今回は勉学のために、Eq型クラスと一貫性のない__不完全なOrd型クラス__を実装した場合についても考えてみました。実際には、多少の制限を許容するのであれば、__不完全なOrd型クラス__び方が便利なことも多いです。
オリジナルの演算子を作ってみる
上の話で、eq a b == trueとなる条件とcompare a b == EQとなる条件が異なる__不完全な__実装が可能であることを理解しましたが、前者を表す演算子==は存在しますが、後者を表す演算子は定義されていません。そこで、話の便宜上、オリジナルの演算子を作っておきたいと思います。
PureScriptの特徴の1つに、自由に演算子を定義できる点があります。他の言語でも定義済みの演算子の意味をオーバーライドする機能を持つものはありますが、全く新しい演算子を定義する機能がある言語は多くないのではないでないでしょうか。
それでは、2つの値の順位が同順であることを表す演算子~~を作ってみます。これは"だいたい同じ"ことを表す数学記号「$\approx$」をイメージしてみました。
simEq :: forall a. Ord a => a -> a -> Boolean
simEq a b = EQ == compare a b
infix 4 simEq as ~~
この逆の演算子/~も定義してみましょう。今度は数学記号「$\not\approx$」をイメージしました。
notSim :: forall a. Ord a => a -> a -> Boolean
notSim = not <<< simEq
infix 4 notSim as /~
これで、Ord型クラスから生成される全ての順序関係を、演算子だけで表すことができるようになりました。
(注意)
ここで定義した~~や/~と同形の演算子は_purescript-probability_パッケージでも異なる意味で定義されています。これらの演算子は_purescript-numbers_パッケージで定義されている演算子~=(数学記号の「$\simeq$」に対応)で代替可能であり、~=の方が使用頻度が高いと考えられるため、今回は使用頻度の高い方との衝突を避けて~~と/~を同順演算子として独自定義に利用しました。
不完全なOrd型クラスの条件
この節の内容は筆者による見解を含みます。
先ほど作ったオリジナルの演算子を使って、Ord型クラスの満たすべき条件を、もう一度考え直してみましょう。
プログラミングの都合上、__不完全なOrd型クラス__で十分なんてことはよく有ります。しかし、__不完全__とはいっても不完全なりに最低限満たしておくべき性質はあるはずです。そこで、__不完全なOrd型クラス__を実装する際に、最低限満たしておくべき性質について、書き下してみます。
- 反射律の代わりに
$a==b;\Rightarrow;a\sim\sim b$
「同値のものは同順」
$\newcommand{\notsimeq}{\mathbin{,\mathrel/,\sim}}
\newcommand{\noteq}{\mathbin{,\mathrel/,=}}
a \notsimeq b;\Rightarrow;a \noteq b$
「同順でないものは同値ではない」
- 反対称律の代わりに
$a<=b\;\Rightarrow\;b>=a$
「aがb以下ならば、bはa以上」
$a <= b \;\text{and}\; b <= a \;\Rightarrow\; a \sim\sim b$
「aがb以下で、bがa以下であれば、aとbは同順」
- 推移律も書き換えて
$a <= b \;\text{and}\; b <= c \;\Rightarrow\; a <= c$
「aがb以下で、bがc以下であれば、aはc以下」
$a \sim\sim b ;\text{and}; b \sim\sim c ;\Rightarrow; a \sim\sim c$
「aとbが同順で、bとcが同順なら、aとcも同順」
これを書きたかったので、わざわざ新しい演算子を作ってみました。個人的な見解であり、数学的に裏付けたわけでもないので、不備があるかもしれませんが、おおよそこのくらいの性質を保証できれば、プログラミングとしては十分ではないでしょうか。
普段のプログラミングでも、たまに、イコール条件と同順条件が異なる実装をしたくなることがありますが、少なくとも、私は、上記条件が満たされるようにする事で、不自然な挙動にならないように気をつけています。今回は、わざと変な例を作りたかったので、この辺りを気をつけながら実装してみました。
何でも比べられるとは限らない!?
ところで、ここまでの話の中で、前回の話でEq型クラスの例として最初に紹介したPointデータ型が出てこなかったことに、気づかれましたでしょうか?これは、忘れているわけではなく、意図的に避けていたのです。なぜなら、Pointデータ型に対しては一般的な大小関係を定義できないからです。
Pointデータ型は2次元の座標点を表すデータ型でした。一方で、大小関係というものは1次元的な性質の概念なので、Pointデータ型に一般的な大小関係を定義するのは自然な行為ではありません。__等しいか等しくないか__を判断できることと、__大きいか小さいか__を判断できることは別の概念なのです。
しかしながら、用途によっては2次元的なデータ型に対して、大小関係を定義したいこともあるでしょう。そんな時に便利なのがcomparing関数です。
comparing 関数
comparing関数を使うと、一般的な大小関係を定義できないデータ型であっても、特定の用途に限定された大小関係を判定できます。comparing関数は次のように宣言されています。
comparing :: forall a b. Ord b => (a -> b) -> (a -> a -> Ordering)
要するに、Ord型クラスを実装できないのであれば、Ord型クラスが実装された別のデータ型に変換する関数f :: a -> bを定義してやれば良いのです。
用途の限定された大小関係1
例えば、原点からの距離を計算する関数f1と、それに基づいて大小関係を判定する関数g1を次のように定義してみます。
f1 :: Point -> Number
f1 (Point x y) = sqrt (x * x + y * y)
g1 :: Point -> Point -> Ordering
g1 = comparing f1
すると、次のようにPointデータ型を比較することができるようになります。
> g1 (Point 0.0 0.0) (Point 1.0 1.0)
LT
> g1 (Point (-1.0) (-1.0)) (Point 1.0 1.0)
EQ
> g1 (Point 1.0 (-2.0)) (Point 1.0 1.0)
GT
用途の限定された大小関係2
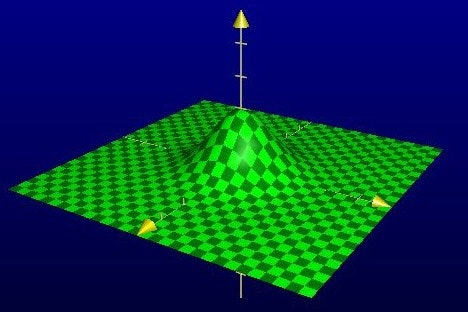
あるいは、座標点$(x,y)$の標高を計算する関数f2と、それに基づいて大小関係を判定する関数g2を次のように定義してみます。
f2 :: Point -> Number
f2 (Point x y) = exp $ negate (x * x + y * y)
g2 :: Point -> Point -> Ordering
g2 = comparing f2
ここで定義したf2は原点周辺だけが盛り上がった山のような曲面を表す関数です。縮尺を多少調整していますが、こんなイメージです。
すると今度は、別の比較結果を得ることができます。
> g2 (Point 0.0 0.0) (Point 1.0 1.0)
GT
> g2 (Point (-1.0) (-1.0)) (Point 1.0 1.0)
EQ
> g2 (Point 1.0 (-2.0)) (Point 1.0 1.0)
LT
このように、comparing関数を用いると、Ord型クラスが定義されていないデータ型に対しても、用途に応じた比較演算を行うことが可能になります。
小さくたってピリリと辛い
今回は、Ord型クラスについて学んでみましたが、どうだったでしょうか? 普段、無意識に理解している__大きいか小さいか__という概念も、改めて考えてみると奥が深かったりします。次回からは、Ord型クラスから派生する型クラスについて見ていきましょう。それでは、また次回。
演習問題
前回作成したWeightデータ型にOrd型クラスを実装してみてください。
参考文献
Ord型クラスについては下記を参考にしました。
- https://pursuit.purescript.org/packages/purescript-prelude/3.1.0/docs/Data.Ord
- https://github.com/purescript/purescript-prelude/blob/v3.1.0/src/Data/Ord.purs
順序集合についてては下記を参考にしました。