やりたいこと
波形データを解析するための理屈的な側面を整理すること
やってみた
波形データの一般形
波のデータは、色々なsin波を合成したもの。
sin波といっても、大きさが違うもの、周波数が違うもの、ちょっと横にズレた(いわゆる位相が違う)ものなどがある。
位相がずれたsin波は、sinとcosの和で表現できる。
つまり、
sin(x + φ) = A・sin(x) + B・cos(x)
のように書くことができる。
このことから、どんな波形データも、
F = (a1・sin(x) + b1・cos(x)) + (a2・sin(2x) + b2・cos(2x)) + ・・・
のような形で表現できる。
やりたい解析
sin(2x)の「2」の部分は、いわゆる周波数。なので、a2・sin(2x)でのa2は、「2」の周波数がどれくらいの大きさで入っているかということ。
つまり、波 F に対して、a1、b1、a2、b2、・・・が分かれば、波に含まれている、それぞれの周波数の大きさが分かるということになる。
まずは、この a1、b1、a2、b2、・・・を算出することを目的にする。
解析に用いる手法
例として、周波数 1、2、3 の波の合成波 F
F = 4 sin(x) + 2 sin(2x) + 7 cos(3x)
を例に考える。
sin波(cosもだけど)は、関数の直交という考え方があって、別の周波数の波を掛けて、周波数区間で積分をすると、0になるという性質がある。
つまり、
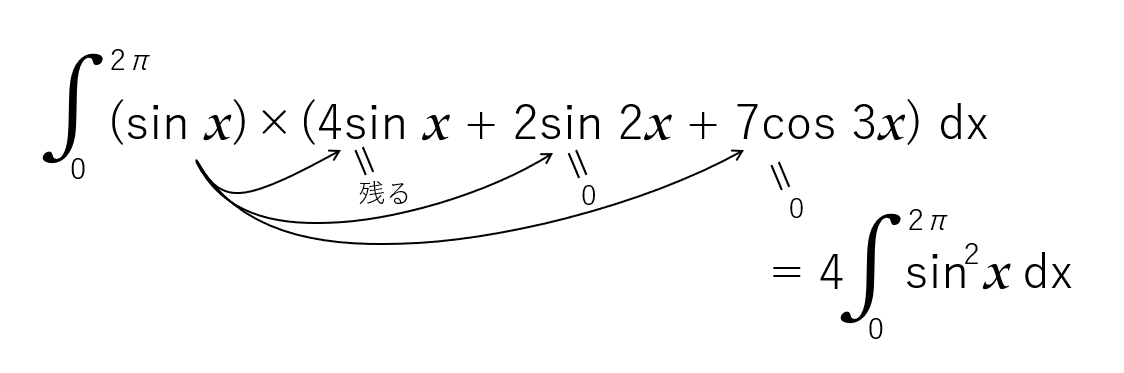
というように、Fに sin(x)を掛けて積分をすれば、sin(x)の係数部分が浮き出てくる。
まず、定積分のロジックを作っておく。
定積分といっても、単に面積を算出するだけなので、
データ列から細切れの面積を出して足し合わせる。
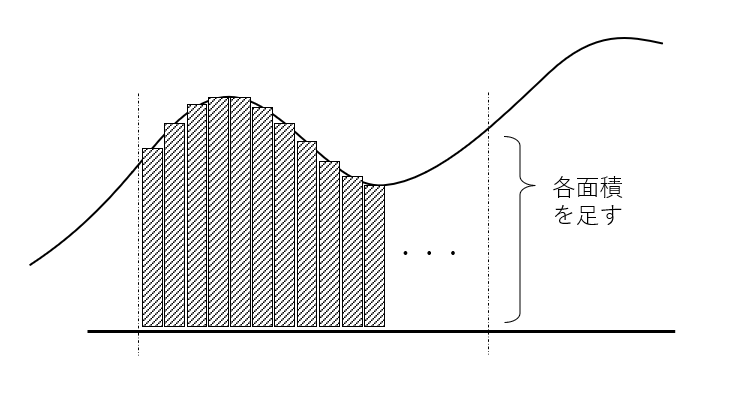
また、シンプルなsin波の半周期の面積が1になるように調整しておく(これは単に好みの問題)。
# -*- coding: utf-8 -*-
import math
def definite(arr, smpl, stsec, edsec):
"""
定積分処理
振幅1のsin波 1/2周期分で、値が1となるように調整済
Parameters
----------
arr: numpy.ndarray
積分するデータの列
smpl: float
サンプリングレート
stsec: float
積分開始秒数
edsec: float
積分終了秒数
"""
stidx = int(stsec * smpl)
edidx = int(edsec * smpl)
res = 0
for x in range(stidx, edidx + 1):
res += (arr[x] * (1 / smpl) * math.pi)
return float('{:.03f}'.format(res))
次に、
・ 同じ周波数の波を掛けて積分しても残ること
・ 違う周波数の波を掛けて積分すると0になること
を検証しておく。
# -*- coding: utf-8 -*-
import sys
sys.dont_write_bytecode = True
import Dummy as dmy
import Integral as Itg
def main():
smpl = 1024
sec = 1
r = 1.0
# sin(x)
sinx = dmy.makeWave(1, smpl, sec, r, 0, 1)
# cos(x)
cosx = dmy.makeWave(1, smpl, sec, r, 1, 0)
# sin(2x)
sin2x = dmy.makeWave(2, smpl, sec, r, 0, 1)
# sin(x) を 0~0.5秒 で積分 -> 1になるハズ
area_sinx = Itg.definite(sinx, smpl, 0, 0.5)
print("sin(x) = " + str(area_sinx))
# sin(x) * sin(x) を 0~0.5秒 で積分 -> 0以外になるハズ
area_sinx_pow2 = Itg.definite(sinx * sinx, smpl, 0, 0.5)
print("sin^2(x) = " + str(area_sinx_pow2))
# sin(x) * cos(x) を 0~0.5秒 で積分 -> 0になるハズ
area_sinx_cosx = Itg.definite(sinx * cosx, smpl, 0, 0.5)
print("sin(x)*cos(x)=" + str(area_sinx_cosx))
# sin(x) * sin(2x) を 0~0.5秒 で積分 -> 0になるハズ
area_sinx_sin2x = Itg.definite(sinx * sin2x, smpl, 0, 0.5)
print("sin(x)*sin(2x)=" + str(area_sinx_sin2x))
return
if __name__ == '__main__':
main()
ここまで来たら、上に書いた
F = 4 sin(x) + 2 sin(2x) + 7 cos(3x)
を例に、各周波数の係数を取り出してみる。
import math
import numpy as np
import Integral as Itg
def ft(wav, smpl, sec, freq):
"""
各係数を取得
Parameters
----------
wav: numpy.ndarray
解析するデータ列
smpl: int
データ列のサンプリングレート
sec: (float, float)
解析開始秒数、解析終了秒数
freq: (int, int)
解析開始周波数、解析終了周波数
"""
stidx = int(smpl * sec[0])
edidx = int(smpl * sec[1]) + 1
anawav = wav[stidx:edidx]
res_sin = []
res_cos = []
stfreq = freq[0]
edfreq = freq[1]
for f in range(stfreq, edfreq + 1):
sinx = makeSin(smpl, (sec[1] - sec[0]), 1, f)
cosx = makeCos(smpl, (sec[1] - sec[0]), 1, f)
s_sin_p2 = Itg.definite(sinx * sinx, smpl, 0, (sec[1] - sec[0]))
s_cos_p2 = Itg.definite(cosx * cosx, smpl, 0, (sec[1] - sec[0]))
a_sin = Itg.definite(sinx * anawav, smpl, 0, (sec[1] - sec[0])) / (s_sin_p2 if s_sin_p2 != 0 else 1)
a_cos = Itg.definite(cosx * anawav, smpl, 0, (sec[1] - sec[0])) / (s_cos_p2 if s_cos_p2 != 0 else 1)
res_sin.append(float('{:.03f}'.format(a_sin)))
res_cos.append(float('{:.03f}'.format(a_cos)))
return (res_sin, res_cos)
def makeSin(smpling_rate, sec, r, freq):
"""
sin波の生成
"""
fnc = lambda n: math.sin(n)
res = makeWave(smpling_rate, sec, r, freq, fnc)
return res
def makeCos(smpling_rate, sec, r, freq):
"""
cos波の生成
"""
fnc = lambda n: math.cos(n)
res = makeWave(smpling_rate, sec, r, freq, fnc)
return res
def makeWave(smpl, sec, r, freq, fnc):
res = []
for t in range(smpl * sec + 1):
theta = 2.0 * math.pi * freq / smpl * t
y = r * fnc(theta)
res.append(y)
res = np.array(res)
return res
# -*- coding: utf-8 -*-
import sys
sys.dont_write_bytecode = True
import Dummy as dmy
import Analyze as ana
def main():
smpl = 44100
sec = 1
r = 1.0
# sin(x)
sinx = dmy.makeWave(1, smpl, sec, r, 0, 1)
# sin(2x)
sin2x = dmy.makeWave(2, smpl, sec, r, 0, 1)
# cos(x)
cos3x = dmy.makeWave(3, smpl, sec, r, 1, 0)
f = 4 * sinx + 2 * sin2x + 7 * cos3x
res = ana.ft(f, smpl, (0, sec), (1, 3))
print("sinの係数", end=" ")
print(res[0])
print("cosの係数", end=" ")
print(res[1])
return
if __name__ == '__main__':
main()
微妙な誤差もあるけれども、波のデータ列に対して、各周波数 sin(nx)、cos(nx)を掛けて、その周期区間で積分すれば、各周波数毎の係数を取り出すことができることが分かった。
